Latent Dirichlet Allocation via Collapsed Variational Inference

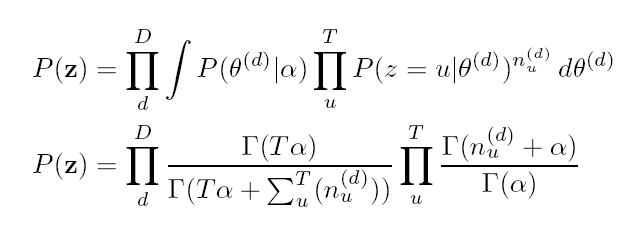
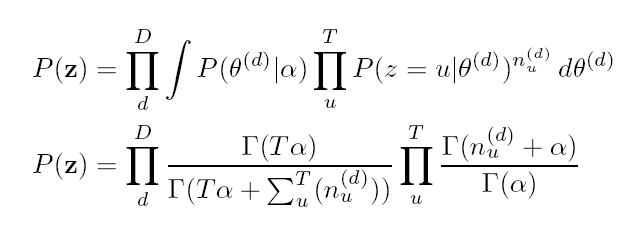
Multivariate Polya

Overview

This software implements Collapsed Variational Bayesian (CVB) inference [1] for the LDA model [2] of discrete count data. The code is based on the Teh et al paper [1], and also uses some practical implementation details kindly provided by the authors on the extremely helpful topic-models mailing list.

The code implements the collapsed variational inference for LDA as a Python C extension module.

DISCLAIMER

Importantly, I wrote this code as an educational exercise for my own benefit only. This software has no connection with [1] or its authors whatsoever. Any errors contained herein are my own.

Code

cvbLDA on github

Requirements

To build and install the module, you will need: See README.txt for further details.

Example usage

from numpy import *
from cvbLDA import cvbLDA

# Model params
(T,W) = (3,5)
alpha = .1 * ones((1,T))
beta = .1 * ones((T,W))

# Dataset
docs_w = [[1,2],[1,2],[3,4],
          [3,4],[0],[0]]
docs_c = [[2,1],[4,1],[3,1],
          [4,2],[5],[4]]

# Stopping conditions for inference
(maxiter,convtol) = (10,.01)

# Do CVB inference for LDA
(phi,theta,gamma) = cvbLDA(docs_w,docs_c,alpha,beta,
                           maxiter=maxiter,verbose=1,convtol=convtol)

Questions/Comments/Bugs

Open up your Python interpreter and e-mail me at: 
'@'.join(['andrzeje','.'.join(['cs','wisc','edu'])])

Reference

[1] A Collapsed Variational Bayesian Inference Algorithm for Latent Dirichlet Allocation
Teh Y.W., Newman D., and Welling, M.
Advances in Neural Information Processing Systems (NIPS) 19, 2007.

[2] Latent Dirichlet Allocation
Blei, D. M., Ng, A. Y., and Jordan, M. I.
Journal of Machine Learning Research (JMLR), 3, Mar. 2003, 993-1022.