CS 368-4 (2012 Fall) — Day 12 Homework

Due Thursday, December 6, at the start of class.

Goal

Create a pretty image by running a Mandelbrot generator on several “tiles”, which can stitched together to create a single, large image.

Essentially, this is an exercise in parameter sweeps, both writing the Python code that defines the tiles and then generating the HTCondor submit file.

Background Information

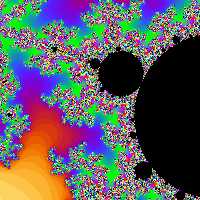
The Mandelbrot set is a mathematical construct that can be used to create pretty pictures. Here is one image that I created from my homework solution:

Running goatbrot

We are not going to write the code to generate the images, as much fun as that might be… Instead, we will use a separate program, goatbrot, to generate the image tiles. The challenge is to run goatbrot with the right command-line arguments, so that we can stitch together the resulting tiles into a single image.

Here is a typical set of command-line arguments to the goatbrot program (these particular arguments should generate the image above without any tiling):

goatbrot -s 600,600 -c -0.70625,0.35625 -w 0.0625 -i 1000000 -o mandelbrot.ppm

The arguments are as follows:

If you want to learn more about the program, check out its website and/or run the following command on our submit machine:

/usr/local/bin/goatbrot -h

Tiles

Now, consider what happens when we want to generate the same image but to spread out the work by dividing the one big square into smaller square tiles. For example, if I create 2×2 tiles, I would get the following four images (black border lines added for clarity, not part of images):

We can identify our tiles two different ways. First, we can assign numbers to rows and to columns (each counting from 0, of course, because we are programmers!), and identify a given tile by its row and column numbers. Here is a diagram of (row, column) numbers for our 2×2 tiling:

And then for the stitching program, it is useful to assign each tile a unique serial number in order. The tile numbers start at the upper-left corner, and increment as we count from left-to-right, top-to-bottom. Here is a diagram of the tile numbers for our 2×2 tiling:

Calculating Tile Arguments

Given a set of Mandelbrot coordinates (center and width), the number of tiles, and the overall image size in pixels, it is possible to calculate all of the command-line arguments to the goatbrot program for each tile. For example, the four goatbrot commands used to produce the image tiles above are:

goatbrot -s 200,200 -c -0.721875,0.371875 -w 0.03125 -i 1000000 -o tile-1.ppm
goatbrot -s 200,200 -c -0.690625,0.371875 -w 0.03125 -i 1000000 -o tile-2.ppm
goatbrot -s 200,200 -c -0.721875,0.340625 -w 0.03125 -i 1000000 -o tile-3.ppm
goatbrot -s 200,200 -c -0.690625,0.340625 -w 0.03125 -i 1000000 -o tile-4.ppm

The necessary math is summarized below. First, we need to define some values:

• cx is the x coordinate (in Mandelbrot space) of the overall image center (e.g., -0.70625 above)
• cy is the y coordinate (in Mandelbrot space) of the overall image center (e.g., 0.35625 above)
• w is our total desired width (e.g., 0.0625 above)
• n is the number of tiles in each dimension (e.g., 2 above)
• p is the size of our output image, in pixels (e.g., 400 above)
• r is the row number of the current tile (0 to n–1, top-to-bottom)
• c is the column number of the current tile (0 to n–1, left-to-right)

Here is how to calculate each argument to goatbrot for the tile at (r, c):

• The -s argument takes the width and height of the tile image, separated by a comma (and no whitespace). Our tiles are square, so both values are the same, and are calculated as the total pixel size divided by the number of tiles, or p / n.
• The -c argument takes the x and y coordinates of the tile’s center point, in Mandelbrot space. The x coordinate for the tile at (r, c) is calculated as:

  cx + (w/n) × (c – ((n–1) / 2))

  The y coordinate is calculated as:

  cy + (w/n) × ((n–r–1) – ((n–1) / 2))

  Note the inversion of r in the second formula, and also note that both the (w/n) and ((n–1) / 2) terms are constant with respect to r and c and hence can be calculated just once and then used for all tiles.

• The -w argument takes a single width for the image, in Mandelbrot coordinates. It is calculated as the total desired width divided by the number of tiles, or w / n.
• The -o argument includes the tile number, which is calculated as rn + c.

See below for advice on setting the -i option and on formatting the -o option.

Tasks

Armed with all of that background information, your task is to write a Python script that will prepare a set of HTCondor jobs to produce a corresponding set of Mandelbrot image tiles. At the end of the assignment, I will show you the command to stitch the image files together; for now, you will need to run this command by hand after all of the HTCondor jobs finish.

Your script will need to take a bunch of arguments that define what to draw:

./homework_12.py -0.70625 0.35625 0.0625 400 2

The arguments, in order, correspond to our mathematical values above:

• cx (Mandelbrot center x)
• cy (Mandelbrot center y)
• w (Mandelbrot width)
• p (pixel size)
• n (tiles per size)

Note: Your script must work with other values for these arguments! The values above match the examples in the Background section, so that you can check your work, but I should be able to run your script with any reasonable input values. Nonetheless, is is probably best to use tile dimenions (n) that are powers of 2, and to use image sizes (in pixels) that are evenly divisible by the tile dimenions.

With that information, your script can prepare the HTCondor jobs and perhaps even offer to submit them. If you would like some further suggestions for doing this assignment, keep reading; otherwise skip to the next section.

Some thoughts on how to approach this assignment:

1. Do some design work first. Mostly, try to answer questions like the following:
   • Which of the three approaches outlined in class to doing a parameter sweep fits best here?
   • Will your script be capable of submitting the HTCondor jobs?
   • If so, how will the user tell the script to submit?

   For the first question, note that it is best to have all of the output files (one from each job) end up in the same dircetory. Doing so makes it easier to stitch all files together into a single image.

2. For the coding, start by trying to write the code that iterates through all of the tiles. How many parameters do you have? What does each one mean? What is each one’s range (start, stop, step)? Try to stick with simple integer parameters — as seen above, we can calculate the actual command-line arguments to goatbrot from simple integers.
3. For each value of your parameter(s), call a function, say, compute_arguments, which takes your parameter(s) as arguments. For now, have the function simply print the parameter(s), so you can check them.
4. Now, expand compute_arguments so that, instead of simply printing the parameter(s), it returns a single string which is the complete set of goatbrot command-line arguments that correspond to the parameter(s). Check your arguments against the examples above, and make sure that your code works in other cases, too.

   For the number of iterations to run, just pick a number. Unless you use very small values for w (and hence zoom in deeply into the image), a number around 10000 will work fine. Even an iteration count of 1000000 (1 million) runs quite fast in most cases.

   Name your output files so that they sort in the correct tile order, shown above. Do this by including the tile number itself in the filename. For longer tile numbers, pad the tile number with leading zeroes, which is easy with the % formatting codes:

   output_filename = 'tile-%04d.ppm' % (tile_number)

5. The rest is easy: Make your script generate your submit file(s) and any other files needed, then (optionally) submit the submit file(s).

   Important note: In your submit file, make sure the executable line is exactly as follows:

   executable = /usr/local/bin/goatbrot

Stitching Your Image Tiles

Once you have your output files, it would be nice to stitch them together to see the whole image. For now, just do this by hand. On our submit machine, run the following command in the directory that contains your PPM output files:

montage tile-*.ppm -mode Concatenate -tile 2x2 homework-12.png

Be sure to replace the 2x2 part with the exact number of tiles (horizontal and vertical) that you used. Also, the homework-12.png filename is the output filename of the stitching step, and so it can be whatever you like.

Copy the resulting final image file back to your own computer and open it in a graphics program or a web browser. Did it turn out OK? If the tiling looks wrong, then go back over your script, your output filenames, and your montage command for errors.

Explore different coordinates (center point and width arguments) with your script. Send your favorite coordinates and/or best single image to the group mailing list, if you like! If you do so, please restrict your emailed image sizes to 500×500 pixels or so.

Extra Challenges

Some ideas for extra learning:

• Try making your script work for images that are not square. You will need to add command-line arguments to your script, and it makes some aspects a bit more complicated. However, the same overall approach should still work.
• Have your script implement more than one approach to preparing the HTCondor jobs. Allow the user to select the approach from a command-line argument. After seeing the files and/or directories of the different approaches, which do you prefer in this case? Why?
• Accept settings and parameter ranges via an input file. Perhaps consider adding other parameters to the sweep. Maybe support a range of widths (and hence the “zoom” factor)?
• For the very adventuresome: Consider writing a script that would produce multiple (final) images that could, with the right software, be sequenced into a short movie. Each individual image should still be tiled. Could you create a series of, say, 10 final images that show panning from one center to another? Or zooming toward or away from a fixed center point? Or even pans and zooms in the same sequence?

Reminders

Do the work yourself, consulting reasonable reference materials as needed. Any resource that provides a complete solution or offers significant material assistance toward a solution not OK to use. Asking the instructor for help is OK, asking other students for help is not. All standard UW policies concerning student conduct (esp. UWS 14) and information technology apply to this course and assignment.

Hand In

All homework assignments must be turned in by email! See the email page for more details about formatting, etc.

For this assignment, you must submit only your Python script.

Please do not include your output files this time!

If you like, also add one or more sets of coordinates that make nice images!