Medial Axis Calculation
CS558 (Spring 2011) HomeWork-IV: Instructor : Prof. Vadim Shapiro, UW MadisonIntroduction:
Medial Axis is an important tool for many applications including shape detection, domain decomposition, and geometric compression. In this homework assignment, I have created 2D medial axis calculation using Jonathan Shewchuck's Constrained Delaunay Triangulation ( Triangle) and robust geometric predicates ( including robust circumcenter calculation).A Pseudo code for Medial Axis is as follows
void MedialAxis( boundaryNodes, medialNodes, medialEdges)
{
// Input:
// vector<Point2D> boundaryNodes; in the anticlockwise direction. In this example we assume that the polygon is closed
// and simple connected;
// Output:
// vector<Point2D> medialNodes; The coordinates of the medial points generated.
// map<int,int> medialEdges; The edges forming the medial axis;
//
// Step: I; using Jonathan Shewchuk's triangle with -pg option. i.e.
vector<Triangle> cdt = getConstrainedTriangulation ( boundaryNodes );
// Step 2: Calculate the circumcenter using Jonathan Shewchuk's exact Circumcenter software
nTriangles = cdt.size();
for ( size_t i = 0; i < numTriangles; i++)
{
Triangle src = cdt[i];
Point2D c = getCircumCenter( src );
// Check that point 'C' is within some triangle of the CDT i.e. it does not fall outside
bool found = getHoldingTriangle( cdr, c, dst );
if( found ){
medialPoint.src = src;
medialPoint.dst = dst;
medialPoint.center = c;
}
}
//Step 3: Get all the edges of CDT;
vector<Edge> meshedges = getEdges( cdt);
size_t numEdges = meshedges.size();
for( size_t i = 0; i < numEdges; i++)
vector<Triangle> edgefaces = getFaceNeighbours( meshedge[i] );
if( edgeface.size() == 2) {
bool found0 = getMedialPoint( edgeface[0], mp0 );
bool found1 = getMedialPoint( edgeface[1], mp1 );
if( found0 && found1 )
medialEdges.push_back( make_pair(mp0.id, mp1,id);
}
}
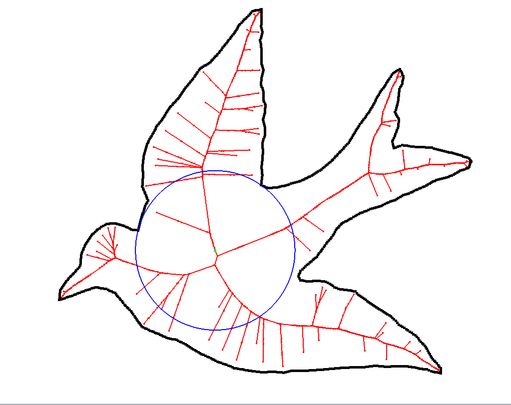 |
Download DataSet |
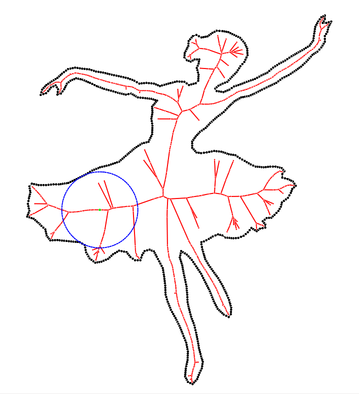 |
Download Dataset |
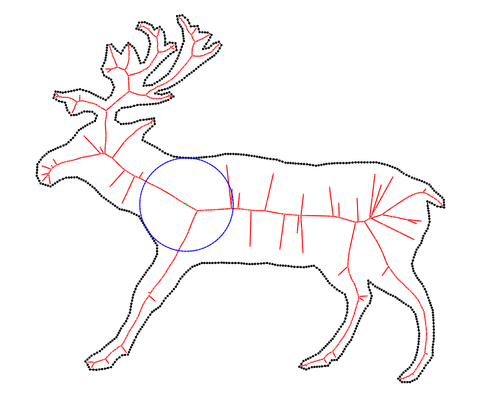 |
Download Dataset |
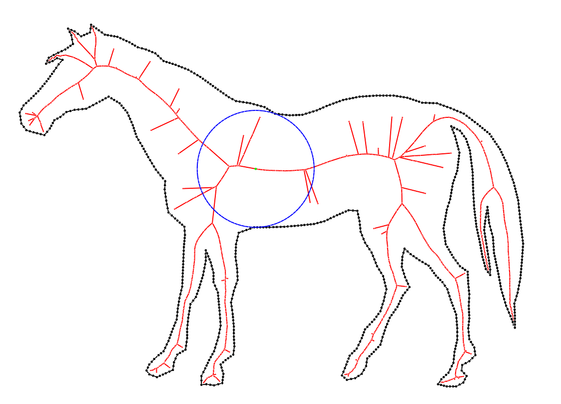 |
Download
dataset |
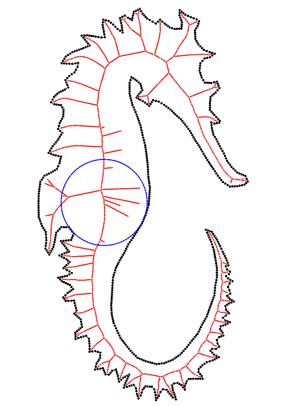 |
Download dataset |
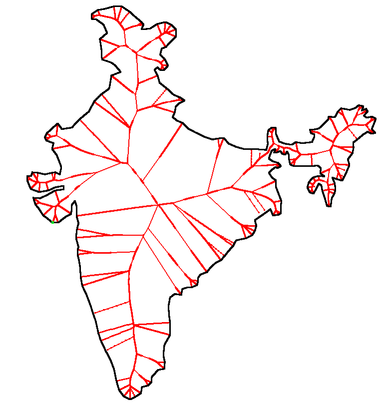 |
Download dataset |