Prim's Algorithm

Overview of Prim's Algorithm

Prim's Algorithm is a method used in graph theory to find the Minimum Spanning Tree (MST) of a weighted, undirected graph. It starts from a random vertex and keeps adding the smallest possible edge to build the MST step by step.

How Prim's Algorithm Works

1. Start with any vertex and add it to the MST.
2. Keep adding the smallest edge that connects a vertex in the MST to a vertex outside of it.
3. Repeat until all vertices are included in the MST.

Pseudocode for Prim's Algorithm

    prim(v):
        pq = new PriorityQueue()
        mark v as visited
        pq.insert(v.outgoingEdges)
        while (!pq.isEmpty()):
            c = pq.removeMin()
            if (c.endNode is unvisited):
                mark c.endNode as visited
                add c to tree
                pq.insert(c.endNode.outgoingEdges to unvisited nodes)
    

Visual Representation of Prim's Algorithm

The following diagram shows how Prim's Algorithm builds the MST step by step:

Further Reading

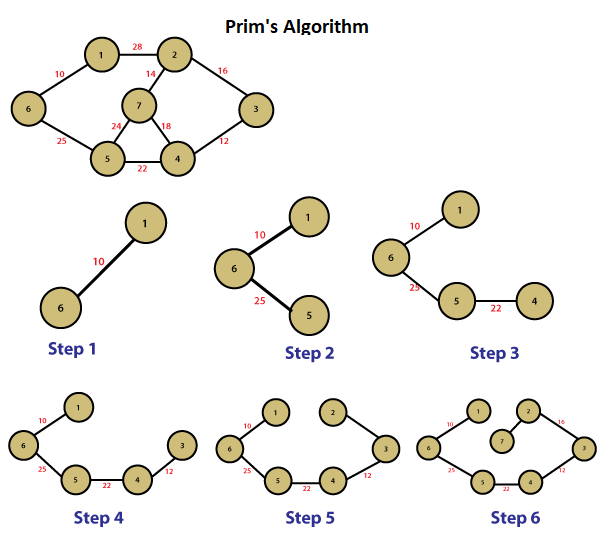
If you'd like to learn more about Prim's Algorithm, check out the link below:

Prim's vs Kruskal's Algorithm

Kruskal's Algorithm is another way to find the MST of a graph. Unlike Prim's, which starts with a vertex, Kruskal's Algorithm sorts all the edges by weight and adds them one by one, making sure no cycles are created. It keeps adding edges until all vertices are connected.