I am a Ph.D. candidate in Statistics at UW-Madison, where I am advised by Professor Sunduz Keles. I work in the fields of machine learning, genomics, and statistical analysis for Next Generation Sequencing Data.
Papers
Fast learning rates with heavy-tailed losses
We study fast learning rates when the losses are not necessarily bounded and may have a distribution with heavy tails. To enable such analyses, we introduce two new conditions:(i) the envelope function sup f∈ F| ℓ◦ f|, where ℓ is the loss function and F is the hypothesis class, exists and is Lr-integrable, and (ii) ℓ satisfies the multi-scale Bernstein's condition on F. Under these assumptions, we prove that learning rate faster than O(n− 1/2) can be obtained and, depending on r and the multi-scale Bernstein's powers.V Dinh, LST Ho, Duy Nguyen, BT Nguyen
Neural Information Processing Systems, NIPS 2016
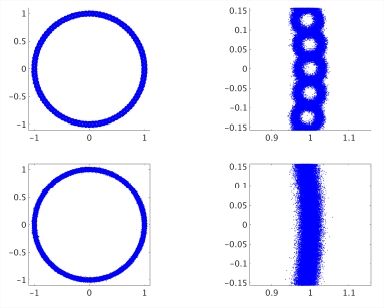
Stochastic Multiresolution Persistent Homology Kernel
We extract topological information from point-cloud objects as a novel feature representation for clustering and classification. Specially, we introduce a Stochastic Multiresolution Persistent Homology (SMURPH) kernel which represents an object's persistent homology at different resolutions. Under the SMURPH kernel two objects are similar if they have similar numbers of and sizes of holes at the same resolutions, even if other aspects of the point-cloud differ. Our multiresolution kernel captures both global topology and fine-grained "topological texture" in the data. Compared to existing topological data analysis methods the SMURPH kernel is computationally feasible on large point-clouds. The kernel can be directly plugged into standard kernel machines, and can be combined with other kernels. We demonstrate SMURPH's potentials with two real-world applications: fundus photography for eye disease classification and wearable sensing for human activity recognition. SMURPH brings new information to machine learning and opens the door for wider adoption of topological data analysis.Xiaojin Zhu, Ara Vartanian, Manish Bansal, Duy Nguyen, Luke Brandl
International Joint Conference on Artificial Intelligence (IJCAI'16), Acceptance rate < 25%
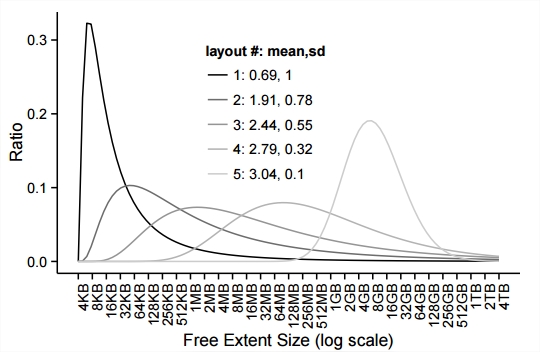
Reducing File System Tail Latencies with Chopper
We present Chopper, a tool that efficiently explores the vast input space of file system policies to find behaviors that lead to costly performance problems. We focus specifically on block allocation, as unexpected poor layouts can lead to high tail latencies. Our approach utilizes sophisticated statistical methodologies, based on Latin Hypercube Sampling (LHS) and sensitivity analysis, to explore the search space efficiently and diagnose intricate design problems. We apply Chopper to study the overall behavior of two file systems, and to study Linux ext4 in depth. We identify four internal design issues in the block allocator of ext4 which form a large tail in the distribution of layout quality. By removing the underlying problems in the code, we cut the size of the tail by an order of magnitude, producing consistent and satisfactory file layouts that reduce data access latencies.Jun He, Duy Nguyen, Andrea C. Arpaci-Dusseau, Remzi H. Arpaci-Dusseau The 13th USENIX Conference on File and Storage Technologies (FAST '15), Acceptance rate 28/130 = 21.5%
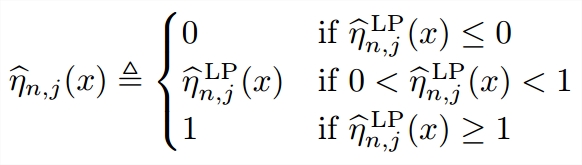
Learning From Non-i.i.d. Data: Fast Rate for the One-vs-All Multiclass Plug-in Classifier
We prove new fast learning rates for the one-vs-all multiclass plug-in classifiers trained either from exponentially strongly mixing data or from data generated by a converging drifting distribution. These are two typical scenarios where training data are not iid. The learning rates are obtained under a multiclass version of Tsybakov's margin assumption, a type of low-noise assumption, and do not depend on the number of classes. Our results are general and include a previous result for binary-class plug-in classifiersV Dinh, LST Ho, NV Cuong, Duy Nguyen, BT Nguyen Theory and Applications of Models of Computation, 2015
Software
Check it out on Github.
Technical Reports
- D. Nguyen, M. Ohashi, A. Wang, E. Johannsen, S. Keles. A non-parametric adaptive test for identifying differential histone modifications from ChIP-seq data. (under revision)
- D. Nguyen, Peter Qian. Sampling Properties of Sudoku-based Space-Filling Designs.
- D. Nguyen. Regression Analysis on Poker Models. (Undergraduate Thesis)
- L. Buggy, A. Culiuc, K. McCall, D. Nguyen. Energy of Graphs and Matrices. (National Science Foundation, REU paper)
Education
| 2012-Present | Ph.D. in Statistics, University of Wisconsin-Madison |
| 2010-2012 | M.S. in Mathematics, Texas Christian University |
| 2007-2010 | B.S. in Mathematics, Summa Cum Laude, Phi Beta Kappa, Texas Christian University |
| 2007-2010 | B.M. in Piano Performance, Summa Cum Laude, Texas Christian University |