Upstream traversal using route_link_sort to find potential secondary crashes and how far they were

• Background

• Problem Definition

• STN data

• Crash records

• Problem definition

• The Algorithm

• Algorithm entry and initialization

• Upstream of routes on the same side

• Upstream of routes on the other side

• Calculate the Actual Distance between Two Crashes

Background (top)

Secondary crashes are one of the major crash types (in terms of the cause of a crash) on interstate highway systems. A secondary crash generally occurred in the queue triggered by a primary incident at a downstream location. Secondary crashes prolong the impact of the primary incidents and degrade both the safety and the efficiency of highway facilities. As a result, countermeasures are desired in reducing the chances of encountering a secondary crash after a primary incident (narrowed down to crash in the following discussion). Such countermeasures could be effectively developed based on analyses of historical crash data. One of the major challenges in analyzing historical crash data is to identify secondary crashes, since explicit information is not always available to indicate whether a crash was secondary or not.

The first step of identifying a secondary crash is to examine whether two crashes were close enough to each other in time and space. If they are, the later crash was potentially a secondary crash of the earlier one. A crash might have caused more than one secondary crash. Literatures have shown many alternatives of judging the closeness between two crashes, and were mainly divided into two categories: 1) static methods and 2) dynamic methods. Static methods use a fixed time threshold (typically 1 hour) and a fixed distance threshold (typically 1 mile) to scope potential secondary crashes of a given primary crash. For example, say given a primary crash C_pri, one identifies a potential secondary crash C_{sec_i} when the highway distance between C_pri and C_{sec_i} is no larger than 1 mile and C_{sec_i} occurred less than 1 hour after C_pri happened. Dynamic methods are similar in concept but prefer to use dynamic distance threshold as time changes. A representative of these dynamic methods is the "progressive curve" proposed by Sun, et al (2006). A "progressive curve" describes the queue length as a function of time, ranged from the occurrence of a primary crash to its full clearance. A "progressive curve" is typically a parabolic-shape curve with a peak. All crashes plotted under the curve are considered secondary crashes of the primary crash.

Static or dynamic, the first step just provides an input to human reviewers to eventually identify actual secondary crashes base on human-but-not-machine readable crash descriptions. Even though, under a computer program's help, the first step significantly reduces human reviewing efforts by filtering out a large portion of the crash base. The rest of this document tries to show an upstream traversing algorithm of finding potential secondary crashes of a primary one, adopting a pair of fixed time and distance thresholds (static method).

Problem Definition (top)

The choice of algorithm highly depends on what data are available. The current study is supported by the WisTransPortal database system, which contains the state trunk highway network (STN) data (updated to 2011) and the crash records (dated from 1994) for the state of Wisconsin.

STN data (top)

The STN data in WisTransportal database consists of a couple of tables. The major tables used for the proposed algorithm are the table of highway reference sites (REF_SITE table), the table of highway links (LINK table), the table of highway routes (RTE table), and the "joined" table of highway link and route (RTE_LINK table). Highway reference sites are reference locations on highways (square-numbered nodes in Figure 1). A highway link is then defined by a "from" reference site and a "to" reference site with direction, representing a uniform segment of highway (any circle-numbered solid arrow in Figure 1). A highway route consists of a sequence of successive highway links (rectangle-labeled dash arrow in Figure 1). For each route, along its traveling direction, the links are sorted by a route_link_sort number. A link's route_link_sort number is smaller than any of its downstream links on the same route, and larger than any of its upstream links on the same route. The circled numbers in Figure 1 can be treated as route_link_sort numbers for illustration purposes (but are actually link ID's). A distinction has to be made here that, a link ID is not a route_link_sort number. One link must have exactly one link ID, which is a unique and unreusable integer. On the other hand, a same route_link_sort number may be used by two different links on different routes, and a link can have different route_link_sort numbers on different routes.

Crash records (top)

For each crash happened on STN, there is a record in the WisTransPortal database, recording information that includes but not limited to crash date, crash time, link on which the crash happened, and the offset between the link's "from" reference site and the crash location. Figure 1 shows a red star shape to indicate a crash happened on link 3 with a certain offset to the "from" reference site 38.

Problem definition (top)

The problem here is (looking at Figure 1 again), given a crash, how could we find all the links that are partially or totally within an upstream highway distance to the given crash. Upstream includes both directions of the highway (as illustrated in Figure 1). To give a concrete example, in Figure 1, assume links 1, 2, 3, 4, 7, and 9 are each 1 mile long, and link 8 is 2 mile long. Further assume the crash is 0.3 mile offset from reference site 38. Given a highway distance threshold of 1 mile, the links to be found are links 2, 3, 4, 7, and 8, since these links are reachable from the given crash in 1 mile.

The Algorithm (top)

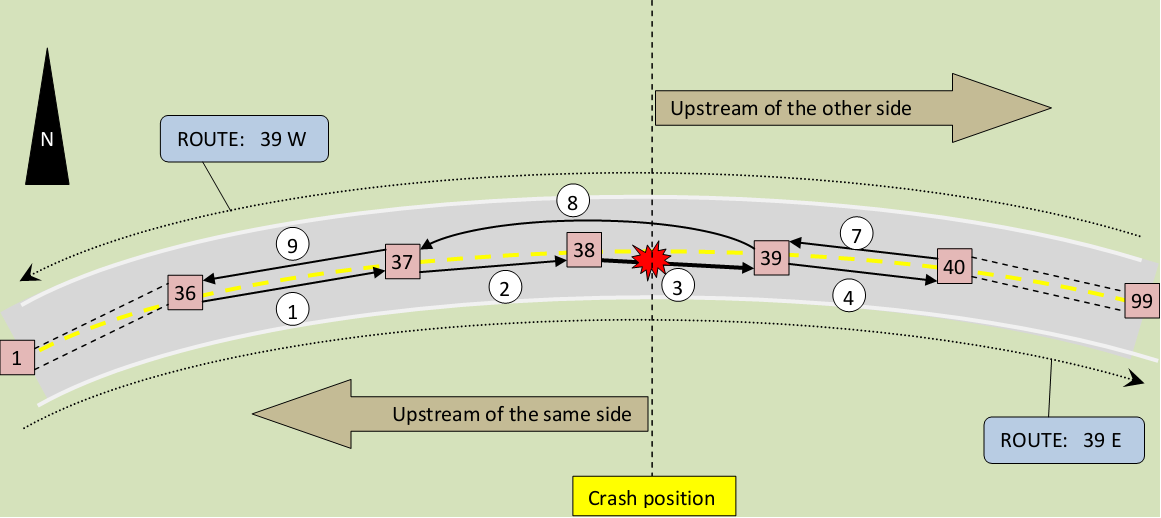
The idea of the algorithm is very straightforward: Given a crash C_pri, one finds the link (Lk_pri) where the crash happened (like link 3 in Figure 1). Starting from Lk_pri, there are two upstream directions to go. The first direction is upstream of all routes on the same side of and heading towards Lk_pri (like route 39E in Figure 1). The second direction is upstream of all routes on the other side of the highway, heading to the opposite direction of Lk_pri (like route 39W in Figure 1). The upstream traversals of these two directions are explained and pseudo-coded in the following subsections.

Before moving onto the algorithm, we define the following global variables that can be accessed by all functions:

• result:
  A growing list of desired result items. Each item in this result list is a data structure that associates a link (Lk_i) with its cumulative distance (CumDist_i) to the primary crash C_pri. CumDist_i is defined as the distance from Lk_i's "to" reference site to the crash location, positive if upstream and negative if downstream.
• dfilter:
  The distance threshold from the location of C_pri.
• routesSameSide:
  A growing list of routes on the same side of Lk_pri that are under traversal.
• routesOtherSide:
  A growing list of routes on the other side of Lk_pri that are under traversal.

Algorithm entry and initialization (top)

The algorithm starts from Lk_pri itself. The cumulative distance of Lk_pri is the offset of C_pri minus the length of Lk_pri. After that, all the routes that contain Lk_pri are retrieved using the RTE_LINK table. For each of such routes (Rt_i), the algorithm calls a function upstreamSameSide(), which takes a route, the closest upstream link of C_pri in that route, and the corresponding cumulative distance of that link as inputs and recursively propogates the traversal to other merged-in routes and routes on the other side. The algorithm entry, initialization, as well as the triggering of successive recursive functions are pseudo-coded as below:

upstreamTraversal(){
	
	cum_dist_init = offset of Cpri - length of Lkpri;
	
	find all the routes that contain Lkpri,
	for each of such routes, say Rti {
		upstreamSameSide(Rti, Lkpri, cum_dist_init);
	}
}

The upstreamSameSide() function and all functions it will directly and indirectly call are explained in the following subsections.

Upstream of routes on the same side (top)

What the upstreamSameSide() function does is to handle each upstream link of a route (route_next) starting from a given one (link_next), until the cumulative distance exceeds the distance threshold. link_next is the closest upstream link of C_pri that is contained by route_next. To go upstream in route_next, the link_sort number is used decreasingly. The cumulative distance of link_next (cum_dist_next) is given as a starting point of further distance cumulation.

upstreamSameSide(route_next, link_next, cum_dist_next){
	
	add route_next to routesSameSide;
	
	route_cur = route_next;
	link_cur = link_next;
	cum_dist_cur = cum_dist_next;
	
	do{
		handleSameSide(link_cur, cum_dist_cur);
		cum_dist_cur += length of link_cur;
		link_cur = the next link in route_next with a smaller link_sort number;
	}while(link_cur != NULL and cum_dist_cur <= dfilter)
}

To handle a link link_cur from route route_cur that's on the same side of Lk_pri, the following handleSameSide() function is used. This function first check if link_cur is of smaller cumulative distance than the distance threshold. If yes, the procedure continues, {link_cur, cum_dist_cur} is added to the result. After adding link_cur to the result, additional work has to be done in case link_cur's "from" reference site connects other upstream routes to be consider (e.g., merged-in routes or routes on the other side). In any of these cases, the link whose "to" reference site overlaps with link_next's "from" reference site will serve as a starting link of another execution of the upstreamSameSide() function, together with the route it introduces. The cumulative distance is updated correspondly.

handleSameSide(route_cur, link_cur, cum_dist_cur){
	
	if (cum_dist_cur <= dfilter){
		addToResult(link_cur, cum_dist_cur);
		get all links whose "to" reference site is the same as link_cur's "from" reference site,
		for each of such links, say link_next{
			cum_dist_next = cum_dist_cur + length of linke_cur;
			
			get all routes containing link_next;
			for each of such routes, say route_next{
				if (route_next == route_cur){
					do nothing
				}
				else if (route_next is on the same side of route_cur){
					if (routesSameSide does NOT contain route_next){
						upstreamSameSide(route_next, link_next, cum_dist_next);
					}
				}
				else if (route_next is on the other side of route_cur){
					if (routesOtherSide does NOT contain route_next &&
						length of link_next - cum_dist_next > 0){
						upstreamOtherSide(route_next, link_next, -1*cum_dist_next);
					}
				}
			}
		}
	}	
}

To avoid redundancy, an item is added to the result only when its associated link is NOT YET in the result or the new cumulative distance is smaller than that of an old item with the same link. For the later case, the new item is not actually added, but is the old item updated with the new cumulative distance. This work is performed by using the following addToResult() function.

addToResult(link_cur, cum_dist_cur){
	if (result does NOT contain any item associated with link_cur){
	}
	else{
		get the item that associates link_cur, say {link_cur, cum_dist_old};
		if (cum_dist_old > cum_dist_cur){
			{link_cur, cum_dist_old} = {link_cur, cum_dist_cur};
		}
	}
}

Upstream of routes on the other side (top)

The traversing to the routes on the other side is triggered by the handleSameSide() function at a certain point. After started, the traversing works similarly to that of the routes on the same side. Below is the pseudo code for the upstream traversing of routes on the other side.

upstreamOtherSide(route_next, link_next, cum_dist_next){
	
	add route_next to routesOtherSide;
	
	route_cur = route_next;
	link_cur = link_next;
	cum_dist_cur = cum_dist_next;
	
	do{
		handleOtherSide(link_cur, cum_dist_cur);
		cum_dist_cur += length of link_cur;
		link_cur = the next link in route_next with a smaller link_sort number;
	}while(link_cur != NULL and cum_dist_cur <= dfilter)
}

A minor difference here in function handleOtherSide() (compared to handleSameSide()) is that new routes are never intended to be explored across to another side (the "same side"). This is because routes on another side are either under traversal by the "same side" pass or contain no upstream links of the primary crash.

handleOtherSide(route_cur, link_cur, cum_dist_cur){
	
	if (cum_dist_cur <= dfilter){
		addToResult(link_cur, cum_dist_cur);
		get all links whose "to" reference site is the same as link_cur's "from" reference site,
		for each of such links, say link_next{
			cum_dist_next = cum_dist_cur + length of linke_cur;
			
			get all routes containing link_next;
			for each of such routes, say route_next{
				if (route_next == route_cur){
					do nothing
				}
				else if (route_next is on the same side of route_cur){
					if (routesOtherSide does NOT contain route_next){
						upstreamOtherSide(route_next, link_next, cum_dist_next);
					}
				}
			}
		}
	}	
}

Calculate the Actual Distance between Two Crashes (top)

The above algorithm will terminate with a set of links together with their cumulative distances. Now the question is how to calculate the distance between any crash C_i and C_pri. The answer is as easy as one equation: