Iterated Function Systems

Note: This page uses animated GIFs. You must use a graphical web browser which supports 89a GIFs. If you would like to view each frame of the animation at your own pace, please click on the animation. Clicking on the animation will link you to another page where each frame will be displayed as its own graphic.

Fractals can be formed using Iterated Function Systems. To begin thinking about the topic, let us consider the Cantor Set.

The Cantor Set is formed using the following algorithm:

1. Begin with the set [0,1].
2. Divide the existing segments into thirds.
3. Remove the middle third.
4. Go to step #2.

The picture below should help visualize the process. The solid line at the start of the animation represents the set [0,1]. Each iteration is shown in following frames of the animation. The green highlight indicates the "middle third" which is to be removed. If this process were to be repeated indefinitely, the cantor set would be produced. Obviously, the cantor set cannot be precisely represented with a finite number of pixels on the screen, so a very poor approximation will have to suffice. However, this "poor approximation" will give you a good idea what the cantor set look like (as an uneven spacing of discrete values). Notice how the points tend to cluster. This is one characteristic of the cantor set.

Next, let us focus our attention on the Sierpinski Gasket. As usual, the picture below shows the building of the fractal. We start with an equilateral triangle (although the actual shape does not really matter as we shall see later).

The Sierpinski Gasket can be formed as follows:

1. Begin with an equilateral triangle (although, we can begin with any figure as we will see later).
2. Divide the triangle into four equal-sized triangles.
3. Remove the middle triangle.
4. Go to Step #2.

The above method will form a Sierpinski Gasket. However, it is not an Iterated Function System yet. Let us express this as an Iterated Function System.

1. Begin with an equilateral triangle (again, this is arbitrary)
2. Reduce the image by one-half.
3. Make three copies of the reduced image.
4. Align them in the shape of an equilateral triangle.
5. Translate the top copy to the left above the lower-left copy.
6. Go to step #2.

The following is produced by the above iterated function system:

After seeing a few examples, we are now ready to more precisely define an iterated function system. An initial image is transformed by a set of affine transformations (functions) producing a new image. The new image is then transformed by the same affine transformations producing another new image. Thus, each time the image is transformed, an iteration occurs. If the transformation is contractive--that is, the transformation brings points closer together--, then the image will begin to converge. After infinitely many iterations, assuming a contractive transformation, the image will converge to what is called an attractor.

Let us now look at another Sierpinski Gasket. However, to convince you that the starting shape is arbitrary, let us use a square with half of a diagonal. Below is the resulting IFS Sierpinski Gasket.

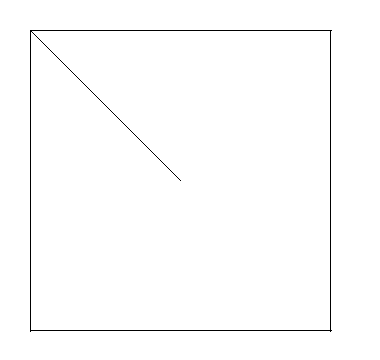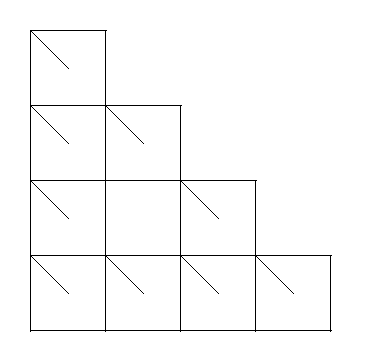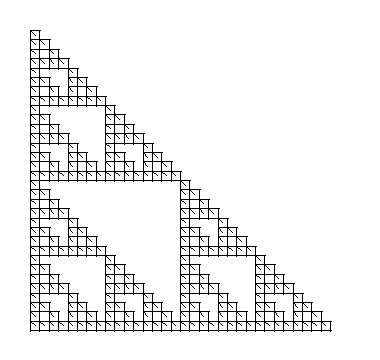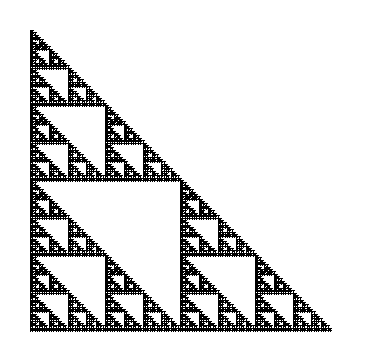
Below are more examples of Iterated Function Systems. As always, click on the picture to see each frame individually.

Dragon

Twin Christmas Trees

Cantor Maze

Snowflake

Twig

Tree

Crystal

Finally, there is one last IFS example to show. However, in this case, the results are not what we would expect. The iterations for Barnsley's fern (named for Michael Barnsley) begin as normal. However, they do not home in on the attractor quickly. It would take a tremendous amount of computing in order to iterate to the attractor as we have done in the previous method. Thus, there must be a better way.

Here is the iterative transformation method for the fern: