CS367 Homework 6
Lecture 1, Spring 2018
Due by 11:59 pm on Friday, May 4, 2018 (not accepted late)

Questions

What do I need to answer?

1. Below is an incomplete definition of the Graphnode class.

   class Graphnode<T> {
    
       private boolean visitMark;
       private List<Graphnode<T>> successors;
    
       public boolean getVisitMark() {
           return visitMark;
       }
    
       public void setVisitMark(boolean mark) {
           visitMark = mark;
       }
    
       public List<Graphnode<T>> getSuccessors() {
           return successors;
       }
   }

   Write the hasSelfCycle method whose header is provided below. This method takes a Graphnode node and returns true iff there exists a path from node to itself (i.e., if there is a cycle in the graph that starts and ends at node). Your implementation must be based on the depth-first search algorithm (i.e., modify DFS to implement hasSelfCycle) and must exit early if possible.

   public boolean hasSelfCycle( Graphnode<T> node )

   You may assume that all the nodes in the graph have been marked unvisited prior to the hasSelfCycle method being called and that there are no self edges (i.e., there are no edges from a node to itself). You may not modify the Graphnode class. You may find it helpful to write an auxiliary method.

2. Given the following graph with nodes having character labels and edges having non-negative integer weights:

   

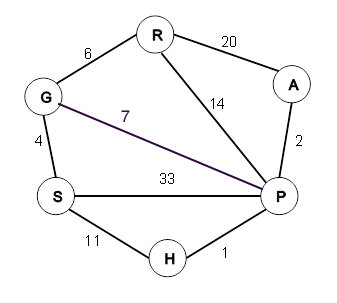
   Trace Dijkstra's algorithm, starting at node S, by filling in the remaining rows in the table below. Each row in the table represents one iteration of the of the algorithm, so use as many or as few rows as needed for the algorithm to complete.

   visited nodes and their shortest distances from start	dist values for nodes in U (only finite values, listed in increasing order)
   -	(0,S)
   S:0	(4,G), (11,H), (33,P)
   S:0, G:4	(10,R), (11,H), (11,P)

   
   
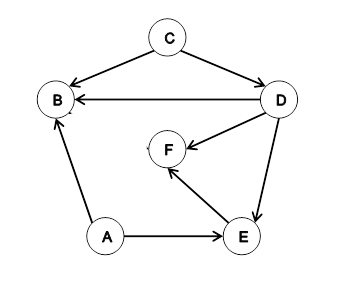
3. Give three distinct topological orderings of the following directed acyclic graph:

Handing in

Please include your name at the top your file.

Put your answers to the questions into one file named Homework6 with the appropriate file extension, e.g., Homework6.pdf (see File Format for acceptable file formats).

Electronically submit your work to the Homework 6 tab on Canvas.