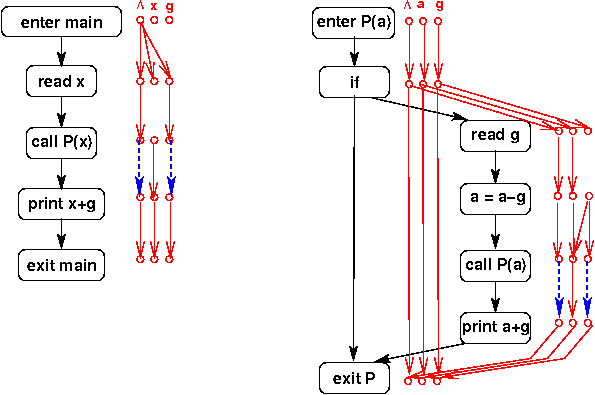
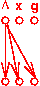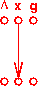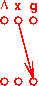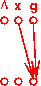Reference Parameters
Finally, let's think about what happens when we allow reference parameters.
In a sense, this introduces two problems:
- The IMOD/IREF sets are not complete because of aliases:
void a( f1, f2 ) {
f1 = f2 + 1;
}
In this example, f1 and all of its aliases are modified;
f2 and all of its aliases are used. The aliases can include
globals (due to a call like: a( g1, g2 )) or other formals (due to a
call like: a( x, x )).
Similarly, any def/use of a global is actually a def/use of the formals
to which it is aliased, too.
- Since a procedure's IMOD/IREF sets are not complete, neither are its
GMOD/GREF sets, which means that incomplete information is propagated
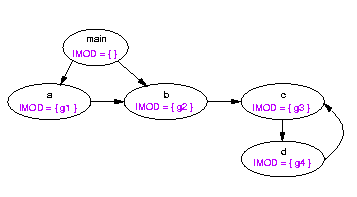
to its callers. For example, here is a call graph in which each node
represents one procedure, the code for that procedure is given in
the node, and the IMOD and GMOD sets that would be computed using a
straightforward extension of
the algorithm used above for value parameters, are shown to the right:
+-------------+
| void main() | IMOD = { }
| call a( g ) | GMOD = { g }
+-------------+
|
v
+--------------+
| void a( f1 ) | IMOD = { }
| call b( f1 ) | GMOD = { f1 }
+--------------+
|
v
+--------------+
| void b( f2 ) |
| f2 = 0 | GMOD = IMOD = { f2 }
+--------------+
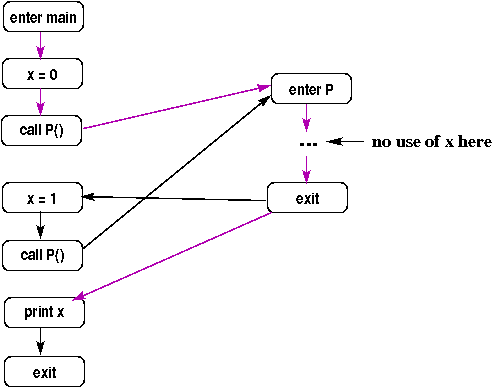
Note that in b, f2 is aliased to g, so b actually modifies g as well as
f2; this is an example of problem 1, discussed above.
However, since b does modify g (due to the call from a), it is also true
that a modifies g. Yet g is not in GMOD(a). This is the example of problem 2.
Surprisingly, it has been shown (by Banning in 1979) that GMOD/GREF sets
can be computed correctly in the presence of reference parameters by breaking
the computation into separate phases:
- Compute DMOD/DREF: modify/use sets that ignore the effects of
aliasing due to reference parameters (essentially the GMOD/GREF sets
computed by the algorithm discussed above for value parameters).
- Compute alias sets for all formal parameters and all globals on a
per-procedure basis:
- Alias(f,p) = {x | x is a formal of p or a global, and is aliased to f}
- Alias(g, p) = {x | x is a formal of p and is aliased to g}
- Combine the results of (1) and (2) to determine:
- What each call may actually define/use (transitively)
- What each def/use of a formal f or a global g may actually
define/use.
Computing DMOD and DREF
The computation of DMOD/DREF is similar to the method for computing GMOD/GREF
given only value parameters; i.e., dataflow functions go on the edges of the
call (multi)graph, and IMOD/IREF sets are propagated back across those edges,
replacing formals with actuals.
Here is an example; the values shown on the edges are the actuals of the
calls that are modified by the called procedure (i.e., the corresponding
formals are in the called procedures' IMOD or DMOD sets):
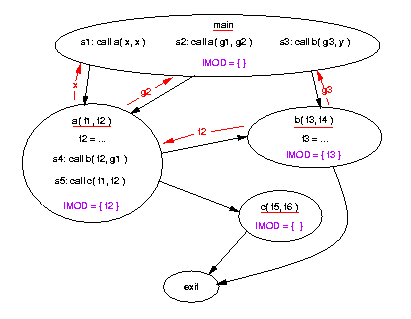 The DMOD sets are:
The DMOD sets are:
s1: { x }
s2: { g2 }
s3: { g3 }
s4: { f2 }
s5: { }
main: { x, g2, g3 }
a: { f2 }
b: { f3 }
c: { }
The next step is to compute the alias sets.
This has been described in the paper "Fast Interprocedural Alias Analysis"
by Keith Cooper and Ken Kennedy, published in the Conference Record of the
Sixteenth Annual ACM Symposium on Principles of Programming Languages (1989).
Alias sets can be computed in two steps:
- Use the "binding graph" to compute formal/global aliases.
- Use the "pair binding graph" to compute formal/formal aliases.
The binding graph for a program includes a node for each formal of each
procedure, and an edge f1 → f2 iff f1 is passed as an actual parameter
in some call to p, and f2 is the corresponding formal of p.
For example, at call site s4 in procedure a of the program shown above,
f2 is the 1st actual, and f3 is the corresponding formal of the called
procedure b. Therefore, in the program's binding graph there would be
an edge f2 → f3.
Here is the complete binding graph for the example program:
f1 f2 f4
| | \
| | \
v v v
f5 f3 f6
To compute the formal/global aliases (for each formal f, which
globals it may be aliased to):
// collapse scc's of binding graph
replace each scc with a representative node n
// initialize
for each node x, set A(x) = {}
for each call site s
for each global v passed to formal f at s
A(f) = A(f) U { v } // if f was in an scc, use the rep. node n for f
// traverse the graph, propagating aliases
for each node f in topological order
A(f) = A(f) U A(g) such that g is a predecessor of f
// set values for all nodes of scc's
for each scc c
for each node f in c
let n be c's representative node in
A(f) = A(n)
For our example, after the initialization step, we'd have the following
initial alias sets
A(f1) = { g1 }
A(f2) = { g2 }
A(f3) = { g3 }
A(f4) = { g1 }
A(f5) = { }
A(f6) = { }
The propagation loop would add g2 to the sets of f3 and f6, and would add
g1 to the set of f5.
Note that this algorithm maps formals to the globals to which they are
aliased (f1 → {g1}, etc.). We also want the sets
"Alias(g,p) = the set of p's formals to which g is aliased in p".
We can get those sets using this algorithm:
for each procedure p
for each global g
set Alias(g,p) = { }
for each formal f of p
for each g in A(f)
add f to Alias(g,p)
After using this algorithm in our example, we get:
Alias(g1, a) = { f1 } Alias(g1, b) = { f4 } Alias(g1, c) = { f5 }
Alias(g2, a) = { f2 } Alias(g2, b) = { f3 } Alias(g2, c) = { f6 }
Alias(g3, a) = { } Alias(g3, b) = { f3 } Alias(g3, c) = { }
Now we need to compute the formal/formal aliases.
This is done using the "pair binding graph".
There are 3 different ways two formals can be aliased:
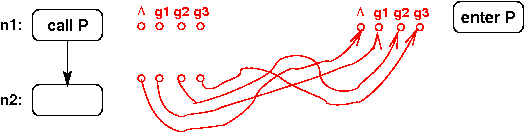
- The same actual is passed to two formals:
+----------------+
| call a( x, x ) |
+----------------+
|
v
+-------------------+
| enter a( f1, f2 ) | f1 and f2 are aliased in a
+-------------------+
- Global g is passed to one formal, an alias of g to another:
+-------------+
| call a( g ) |
+-------------+
|
v
+-----------------+
| enter a( f1 ) |
| call b( f1, g ) |
+-----------------+
|
v
+-------------------+
| enter b( f2, f3 ) | f2 and f3 are aliased in b
+-------------------+
- Formals f1 and f2 are aliases, and are both passed as actuals.
...
|
v
+---------------------+
| enter a( f1, f2 ) |
| call b( x, f1, f2 ) |
+---------------------+
|
v
+-----------------------+
| enter b( f3, f4, f5 ) | f4 and f5 are aliased in b
+-----------------------+
So to identify aliased formals, we must:
- find where formals become aliased
- propagate alias pairs across calls
This is done using the "pair binding graph", which has one node for
each pair of formals of the same procedure, and an edge
(f1, f2) → (f3, f4) iff there is a call that passes f1 to f3 AND passes
f2 to f4, or that passes f1 to f4 AND passes f2 to f3.
Here is the pair binding graph for our example program:
(f1, f2) (f3, f4)
|
|
v
(f5, f6)
Once this graph is created, we identify "initial alias pairs" (formals
that are aliased either because the same actual is passed twice, or because
a global and its alias are passed as actuals) as follows:
for each call site s
if var x is passed to two formals f1 and f2
then {
// same actual passed twice:
// call p(x, x)
// | |
// v v
// void p(f1,f2)
mark (f1,f2)
}
for each actual f that is a formal of the procedure containing s
let f' be the corresponding formal of the called procedure in
for each global g in A(f) that is passed as an actual at s
// global and its alias passed
// call p(f, g)
// | |
// v v
// void p(f',f'')
let f'' be the corresponding formal in the called procedure in
mark (f', f'')
In our running example, only the pair (f1, f2) is marked, because of
the call "a(x, x)" in main.
The next step is to propagate the initial alias pairs by marking
all nodes reachable from a marked node. This can be done as follows:
put all marked nodes (initial alias pairs) on a worklist
while the worklist is not empty
remove pair p from the worklist
for each edge p → q in the pair binding graph
if q is not marked
then {
mark q
put q on the worklist
}
In our running example, node (f5, f6) would be marked (i.e., the initial
alias of f1 and f2 would be propagated to f5, f6, due to the call at call
site s5).
Note that if, in the end, a pair (fj, fk) is marked, it means that
fj and fk may be aliased.
The final step in computing formal's aliases is to combine the results
computed using the binding graph (which globals each formal is aliased to)
with the new results computed using the pair binding graph (which other
formals each formal is aliased to):
for each procedure p
for each formal f of p
Alias(f, p) = A(f) U {f' | (f, f') or (f', f) is marked in the pair binding graph}
Here are the final Alias sets for all globals and formals:
Alias(f1, a) = { g1, f2 } Alias(f1, b) = { } Alias(f1, c) = { }
Alias(f2, a) = { g2, f1 } Alias(f2, b) = { } Alias(f2, c) = { }
Alias(f3, a) = { } Alias(f3, b) = { g2, g3 } Alias(f3, c) = { }
Alias(f4, a) = { } Alias(f4, b) = { g1 } Alias(f4, c) = { }
Alias(f5, a) = { } Alias(f5, b) = { } Alias(f5, c) = { g1, f6 }
Alias(f6, a) = { } Alias(f6, b) = { } Alias(f6, c) = { g2, f5 }
Alias(g1, a) = { f1 } Alias(g1, b) = { f4 } Alias(g1, c) = { f5 }
Alias(g2, a) = { f2 } Alias(g2, b) = { f3 } Alias(g2, c) = { f6 }
Alias(g3, a) = { } Alias(g3, b) = { f3 } Alias(g3, c) = { }
Once alias information is known, we can use it to compute GMOD sets for
every call site and for every procedure:
for each call site s (in procedure p) {
GMOD(s) = DMOD(s)
for each formal and global x in DMOD(s) {
add Alias(x, p) to GMOD(s)
}
}
for each procedure p {
GMOD(p) = DMOD(p)
for each formal and global x in DMOD(p) {
add Alias(x, p) to GMOD(p)
}
}
For our example:
DMOD Aliases Final GMOD
GMOD(s1) = { x } --- { x }
GMOD(s2) = { g2 } --- { g2 }
GMOD(s3) = { g3 } --- { g3 }
GMOD(s4) = { f2 } U Alias(f2, a) = { f2 } U { f1, g2 } = { f1, f2, g2 }
GMOD(s5) = { }
GMOD(main) = { x, g2, g3 } --- { x, g2, g3 }
GMOD(a) = { f2 } U Alias(f2, a) = { f2 } U { f1, g2 } = { f1, f2, g2 }
GMOD(b) = { f3 } U Alias(f3, b) = { f3 } U { g2, g3 } = { f2, f3, g3 }
GMOD(c) = { } --- { }
Note that GMOD(a) does not include g1 even though a modifies f2 and f2 may be
aliased to f1, and f1 may be aliased to g1. The reason is that those two
aliases occur on different calls to a, so their effects are not
combined (and this is correctly reflected in the computed GMOD set)!
Note also that for dataflow analysis, it is the call site
GMOD sets that we would use to define the dataflow function for a
call node, not the called procedure's GMOD set (because the GMOD
set for the call site tells what may be modified as a result of that
particular call, rather than what might be modified by the called
procedure on some call).
Computing Summary Information
The Sharir and Pnueli Approach (Using Phi functions)
The ideas presented here are from a paper called
"Two Approaches to Interprocedural Analysis", by Micha Sharir and
Amir Pnueli,
in a book called Program Flow Analysis, Theory and applications
(edited by S. Muchnick and N. Jones).
The paper makes the following assumptions:
- The program has no locals and no parameters, just global variables.
- Each procedure is represented by a CFG, including edges from a call node
to the node following the call (i.e., the program is not
represented using a supergraph).
- Dataflow functions are associated with CFG edges
(the function on the edge n → m reflects the effect of
executing n). However, there are no dataflow functions on the
edges out of call nodes.
The ideas behind the approach defined by Sharir and Pnueli are as follows;
given a program (a set of CFGs) and a (forward) dataflow problem of interest:
- For each procedure p, for each CFG node n, compute the function
which summarizes the dataflow effects of all same-level,
interprocedurally valid paths in the program from enter p to n;
i.e., the PHI functions include the effects of the procedure calls
that might be made on a path from the enter node to node n.
(A path is valid if call/return edges match; it is same-level if there
is no unmatched call or return edge -- if p is recursive
then there can be non-same-level valid paths, but we don't want the
PHI functions to take those into account).
- Given PHI functions for all nodes, the solution to the dataflow
problem can be computed as follows:
- For the enter node of main, the solution is the special
initial fact "init".
- For all other procedures p, the solution for p's enter node
is the meet of the solutions at all nodes that represent
calls to p.
- For all other nodes n in procedure p,
the solution is the result of
applying n's PHI function to the solution at p's enter node.
- If the dataflow functions are distributive, then the solution is the
meet over all interprocedurally valid paths solution.
- If the dataflow functions are monotonic but not distributive, then the
solution will be less precise, but still safe, and will not include any
facts that arise only from invalid interprocedural paths.
Note that PHI functions are better than jump functions,
because they take into account what actually happens in called
procedures, while jump functions treat calls safely but
pessimistically.
How to use PHI Functions to Solve a Dataflow Problem
As mentioned above, once we have the PHI functions for all CFG nodes,
we can solve a (forward) dataflow problem by computing
the dataflow fact n.val for each CFG node n as follows:
enter-main.val = "init"
for each procedure p:
_ _
enter-p.val = | | c.val // the symbol | | means "meet"
c is a call to p
n.val = PHIenter p, n (enter-p.val)
Note: If the program is not recursive, then these equations can be
solved in one pass using a topological ordering of the call graph.
If the program is recursive, then these equations will be
recursive, too.
In particular, for a recursive procedure p, enter-p.val will depend
on a set of values c.val, and at least some of those will
depend on enter-p.val.
In this case, the greatest fixed point solution can be
found using the usual iterative method:
- Start with all values = top, and all nodes on a worklist.
- While the worklist is not empty:
- remove one node n from the worklist
- recompute n.val
- if the new value is different from the old value, then
put all nodes that depend on n's value in the worklist
Since it is only the enter and call nodes whose equations are mutually
recursive, we can compute the dataflow solutions for those nodes first
(using the iterative algorithm given above),
then use the values computed for the enter nodes to
compute the dataflow solutions for all the rest of the nodes (with no
iteration).
Here is an example program (two CFGs):
enter main enter p
| |
v v
1: x = 0 7: if...
| | \
v | v
2: call p() | 8: x = 3
| | /
v v v
3: x = 2 9: exit
|
v
4: call p()
|
v
5: exit
And here are the PHI functions and final results we'd like to
compute for reaching-definitions analysis: