Register Allocation

Overview
Stack Model (no register allocation)
Sethi-Ullman register allocation (local allocation: within 1 expression)
Semi-global register allocation (within 1 loop)
Global register allocation (across a whole function)
- linear scan
  - overview
  - algorithm
- graph coloring

Overview

The goal of register allocation is to decide which values should be in which registers at which points in the program. We need to consider the fact that:

Some instructions require that certain operands be in registers, and
Even if an instruction permits an operand to be in memory, it will be faster if the operand is in a register.

Ideally, every time a value is used it will be in a register so that we can avoid either loading it from memory or executing a slower "operand in memory" instruction.

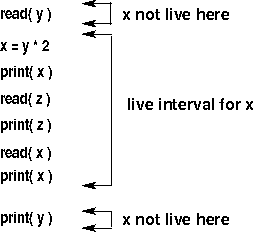
We will consider four approaches to register allocation, ranging from simple but ineffective to more complicated but effective:

The stack model.
Local register allocation (across one expression).
Semi-global allocation (across one loop).
Global allocation (across one procedure).

Stack Model

Using the stack model, values are loaded into registers every time they are needed (i.e., every time they occur as operands of some expression). No values are saved in registers and reused. To generate code for an expression, the expression is represented as a tree and is processed bottom-up:

To process a leaf node (ID or literal):
To process a nonleaf node (i.e., an operator); note that the operands are on the stack, so:

Example

Expression : 2*b+c

Expression tree:

Generated code:

LOAD R1,2	-- Process leaf node "2"
PUSH R1

LOAD R1,b	-- Next leaf node 'b'
PUSH R1

POP R2       --
POP R1	       | Non-leaf node, operator '*'
MUL R1,R2,R1   |
PUSH R1      --

LOAD R1,c	-- Leaf node 'c'
PUSH R1

POP R2       --
POP R1	       | Non-leaf, operator '+'
ADD R1,R2,R1   |
PUSH R1      --

The advantages of this model are that we need only two registers (to hold the operands of a binary operator), and it is very simple and straightforward to implement. However, this approach makes very poor use of registers, no use of instructions that permit one operand to be in memory, and has very high overhead (a push and pop are done for every subexpression).

Sethi-Ullman Register Allocation

Sethi-Ullman register allocation is a local allocation technique; i.e., it works on one expression at a time, making no attempt to save values in registers across expressions. Given an expression represented using a tree, it works in two phases:

Phase 1 labels each tree node with the minimal number of registers needed to evaluate the expression represented by that node's subtree, with no spilling.
Phase 2, given the actual number of registers available, generates code that evaluates the whole expression. If the given number of registers is greater than or equal to the label of the root, the generated code includes no spills, and the number of registers used is equal to the label of the root. If the given number of registers is less than the label of the root, the generated code includes the smallest possible number of spills.

Assumptions

All operators are binary.
Every machine instruction is of the form:
All instructions have 3 forms:
1. Both operands in registers.
2. 1st operand in register, 2nd operand in memory.
3. 1st operand in register, 2nd operand a literal.

Here are some example instructions; note that a register can appear more than once in a single instruction:

  ADD   R1    R2     R3    // R1 = R2 + R3
  ADD   R1    R2     x     // R1 = R2 + x
  ADD   R1    R1     10    // R1 = R1 + 10

Step 1 (Label each node with min # of registers)

Visit nodes bottom-up (only visit a node after visiting all children)
For leaf node:

For non-leaf node t:

		t
	       / \
	    n1:j  n2:k

Example:

		+2
	       /  \
              /    \
             *1     +2
            / \    / \
           a   b  /   \
           1   0 +1    *1
                / \   / \
               a   c d   e
	       1   0 1   0

Step 2 (generate code)

Use the recursive function GenCode defined below, starting with the root of the tree. GenCode's parameters are:

n: a tree node
reglist: the list of available registers
tmp: the index of the next temporary (in case a spill is needed)

GenCode returns the register that, when the code is executed, will hold the value of the expression represented by the tree rooted at node n.

GenCode(n, reglist, tmp) {
	cases (n) of

		x: 1  - Left leaf for var/literal x

			R = First(reglist)
			gen("LOAD R,X")
			return R

		op
	       /  \   - Right child is leaf
	      n1  x:0
			R = GenCode(n1, reglist, tmp)
			gen("op   R,R,x")
			return R

		op
	       /  \   - k<=j and k>0 and k < Length(reglist)
	    n1:j  n2:k
			R1 = GenCode(n1, reglist, tmp)
			R2 = GenCode(n2, reglist - R1, tmp)
			gen("op   R1 R1 R2")
			return R1

			// Note: since k < Length(reglist), there
			// will be enough registers for n2's subtree
			// (with no spills) even with the result of
			// n1's subtree in a register.

		op
	       /  \   - k > j and j < Length(reglist)
            n1:j  n2:k
			// Similar case as above, but do n2 first
			// (Note: in both cases, the subtree that
			// requires *more* registers is processed first).

		op
	       /  \   - Both j and k >= Length(reglist)
            n1:j  n2:k
			R = GenCode(n2, reglist, tmp)
			gen("STORE R T<tmp>")
			R = GenCode(n1, reglist, tmp+1)
			gen("op   R R T<tmp>")
			return R
			
			// Note:
			// The "STORE" code is a spill into a temporary.
			// Another phase of compilation will have to deal with
			// the details of that -- e.g., designating space on
			// the stack for each temporary and replacing
			// references to temporaries with references to the
			// appropriate stack location.
			//
			// The reason for generating code for n2 first, is
			// that we have assumed that only the second
			// operand can be in memory, the first operand
			// must be in a register.  So we generate code
			// for n2 first, spill it to memory, and use
			// that memory location when we do the operation.

	end cases

} // end GenCode

Example expression tree with phase-1 labels:

		+2
	       / \
              /   \
             *1    +2
            / \   / \
           a  b  /   \
           1  0 -1    *1
               / \   / \
              a  c  d   e
	      1  0  1   0

First, consider the code that would be generated for this expression tree if there are at least two registers; i.e., assume that the initial call to GenCode is with reglist = {R1,R2}. Here's the resulting code:

Load R1,a
 -   R1,R1,c
Load R2,d
 *   R2,R2,e
 +   R1,R1,R2
Load R2,a
 *   R2,R2,b
 +   R2,R2,R1

Now consider what happens if there are not enough registers; i.e., if the initial call to GenCode is with reglist = {R1}. Here's the resulting code:

Load  R1,d
 *    R1,R1,e
Store R1,T1
Load  R1,a
 -    R1,R1,c
 +    R1,R1,T1
Store R1,T1
Load  R1,a
 *    R1,R1,b
 +    R1,R1,T1

Semi-global register allocation

This method allocates registers within 1 loop, which may include many basic blocks. The main idea is to choose the values to be kept in registers based on estimating, for each value, how much time would be saved by keeping that value in a register. Nesting level of instructions is taken into account in computing the estimated savings.

To illustrate the approach, consider the following nested loop:

   +->  while (...x...)
   |        |
   |        v
   |      x = w * z
   |        |
   |        v
   |      y = x * w
   |        |
   |        v
   |      while (...z...) <-+
   |      |    \            |
   +------+     v           |
                z = ... ----+

If a variable v is not in a register, then:

each use of v requires a load, and
each definition of v requires a store.

So if the outer loop executes 20 times, and on each iteration the inner loop executes 10 times, then we have the following costs for each variable of not allocating a register for that variable:

	w	x	y	z
# loads	40	41	0	220
# stores	0	20	20	200
total	40	61	20	420

If a load and a store have the same cost, then for this example, we should allocate the variables to registers in the order: z, x, w, y.

Given: R, the number of registers available for allocation, and L the loop in which to do register allocation, use the following technique to choose the "best" R variables to allocate for the whole loop (where "best" means avoids the most dynamic loads and stores).

For each variable v compute the approximate savings if v is in a register:
- savings for v in a single block B:
  saving(v,B) ~= (# uses)*(use cost) + (# defs)*(def cost).
- savings for v in loop L =
  Summation(for all B in L) of [10^(nesting depth(B))*saving(v,B)]
(Note: we could do a better job of computing savings in some cases, e.g.:
- for loops with compile-time bounds
- given profiling information)
Choose the R values with the highest savings.

Note: Once registers have been allocated for each loop, we can use a similar technique to allocate registers in the code "between" loops.

Global register allocation

We will consider two techniques for global register allocation, which works on one (entire) procedure at a time. The two techniques are

Linear Scan: This is the default for LLVM.
Graph Coloring: This is the current state of the art.

Linear Scan

Overview

The linear-scan register allocation algorithm is described in a paper called Linear Scan Register Allocation, by M. Poletto and V. Sarkar. The algorithm works on a linear representation of the program. Different such representations can lead to better or worse register allocation. One possibility is the textual order of the statements. Another is to use an ordering produced by doing a depth-first search of the program's control-flow graph. See the paper for details.

Linear-scan register allocation uses the results of live-variable analysis to create one live interval for each variable. We then try to allocate a register to each live interval; i.e., the corresponding variable is stored in that register throughout the live interval instead of being stored in the procedure's activation record. The live interval for a variable x is the sequence of statements that starts with the first definition of x (the first statement in the linear representation after which x is live) and continues to the last use of x (the last statement in the linear representation before which x is live). Here's an example (showing only the live interval for x, not for y or z):

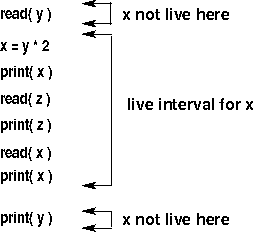
If two live intervals do not overlap, then those variables can use the same register. Note, however, that there may be "holes" in x's live interval where it is in fact not live (that is true in the example above). In this case, it is a waste to have allocated a register to x for the part of the code where it is not live. The algorithm that does register allocation via graph coloring addresses that issue.

Note also that for non-straight-line code, different linear representations can lead to different live ranges (some of which may have more overlap than others). Here's another example, this time in the form of a CFG:

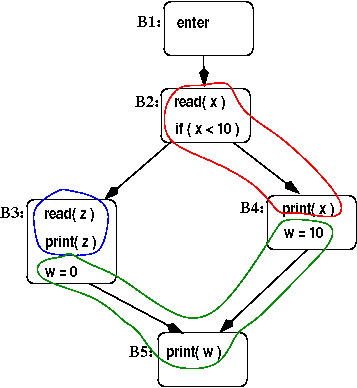
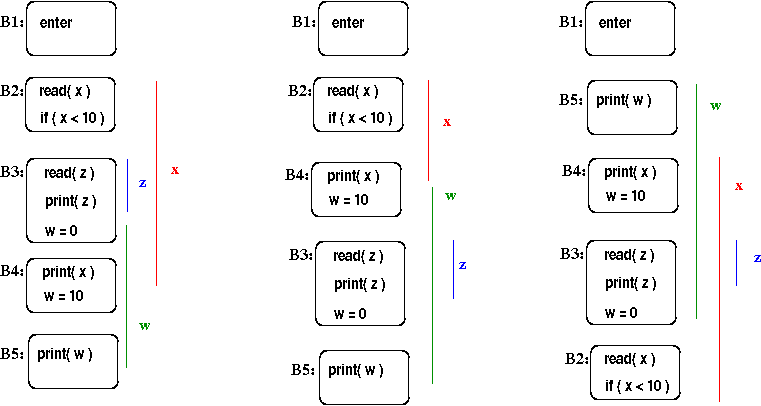
In this example, the colored regions show the statements where each of the three variables (w: green, x: red, and z: blue) are live. We'll have different overlaps between the three variable's live intervals depending on how the 5 blocks are laid out linearly. (If we assume that these are LLVM blocks, which all end with a conditional or unconditional jump to the next block(s), then they can be laid out in any order as long as B1 comes first.) Here are 3 different layouts, with the live intervals shown for the variables in each case.

Linear Scan Algorithm

Now that we understand the basic ideas, here's how the linear-scan algorithm works:

Step 1: Do live variable analysis, and compute live intervals for each variable.

Step 2: Store the live intervals in a list, sorted by their starting points. Here's an example (the start and end points are the instruction numbers in the linear ordering of the code):

In this example, there are 5 live intervals, one for each variable, and each is represented by a horizontal line that shows where the interval starts and ends. Note that the intervals are sorted (top to bottom) by their starting point.

Step 3: Keep a list of available registers, and process each interval in the list in order. As we process the intervals, we also need to keep an active list: this is a list of the intervals that have been given a register, and overlap with the "current" interval. The active-interval list is kept sorted by the end points of the intervals in that list.

Here's how to process one interval:

First, scan the active list to remove all "expired" intervals: When considering the next active interval, if it does not overlap with the current interval (i.e., it is expired) then remove it from the active list and free its register. Stop this scan when you get to the end of the active list, or when the next active interval's end point is greater than the current interval's start point; i.e., that active interval, and all of the ones after it in the active list do overlap the current interval.
After scanning the active list, see if there is an available register (one that was available before removing the expired intervals, or one that was freed because an expired interval was removed from the active list). If yes, then allocate it to the current interval, and add the current interval to the active list. If no, select an interval to be spilled, i.e., an interval that will not get a register. The candidates for spilling are all of the active intervals plus the current interval. One heuristic is to choose the candidate with the largest end point. The intuition is that it will free up its register for the longest time, so maybe several other intervals can be assigned that register.

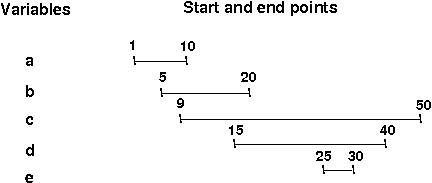
Example: Suppose we start with 2 available registers, and we process the list of live intervals shown above (for variables a, b, c, d, and e). We would start by giving a's interval R1, and putting a's interval on the active list. Then we'd give b's interval R2, and put it on the active list, too. When we process c, there are no expired intervals, and no more registers. Using the heuristic given above (spill the interval with the largest end point), we'd spill c's interval.

Next, we process d's interval. Now we find that a's interval is expired, so we remove it from the active list and free its register (R1), so we can give R1 to d's interval.

Now we process e's interval. This time, b's interval is expired, so again we are able to allocate a register to the current interval.

Now we're done, with this allocation of registers to intervals:

Graph Coloring

Register allocation via graph coloring, like linear-scan register allocation, considers allocating registers to variables across a whole procedure. However, it uses live ranges instead of live intervals. This addresses the problem mentioned above with linear scan allocation, namely that if there are "holes" in a variable's live interval, then it can be wasteful to tie up a register for the entire live interval (as illustrated below).

    x = ...;
      .
      .
      .
    use x;
      .    \
      .     => no use of x.  x will be overwritten anyway so we don't need
      .    /                 to keep its value in the register here.
    x = ...;
      .
      .   
      .
    use x;

A live range is a pair of the form: (<variable>, <set of CFG nodes>). A live range for variable x is roughly all of the nodes of the control flow graph starting from a definition of x, up to all the uses of x reached by that definition.

If two live ranges don't overlap then they can use the same register. For example:

        x = ...; -+
          .       |    
          .       |    overlap of live ranges; x and y cannot use the
          .       |    same register
        y = ...; -|--+
	use x;   -+  |
	use y;   ----+
          .
          .
          .
	x = ...; -+ no overlap with preceding live ranges; y could use
	  .       | the same register as this x, or the two x's could
	  .       | use the same register
	  .       |
	use x;   -+

The algorithm for global register allocation via graph coloring consists of 4 steps:

Step 1: Compute live ranges
Step 2: Build the interference graph
Step 3: Color the graph
Step 4: Convert colors to registers

Step 1: compute live ranges

Build the CFG.
Do reaching defs and live variable analysis.
Note: the variables of interest are those that are candidates for registers. Variables that are not candidates might include:
- variables that could be aliased:
  - variables that could be pointed to
  - globals (also, could be changed in calls to functions that won't know which register the global is in)
- array elements (too hard to tell which element is being referred to)
- structs/unions (too big to fit in a register, too hard to deal with individual fields)
- floating-point values (too big to fit in a single register; also, on machines like the Sparc, floating-point registers are not saved across calls)
What's left: locals that are scalar, and not floating point. This might include parameters, though they are sometimes more difficult to handle than "plain" locals.
Build initial live ranges:
- For each CFG node D that defines variable x, the initial live range for D consists of:
  ( <x>, <{D} union {N | x in N.live-before and D in N.reaching-defs-before}> )
  Note: the live range is a pair: the variable defined at D, and the set of nodes in the range.
- Convert initial live ranges to final live ranges (collapse overlapping initial live ranges for the same variable):
```
for each var x
   for each live range R for x
         if there is another live range R' for x such that R intersect R' != {}
         then R "absorbs" R' (i.e. R = R U R', R' goes away)
    
```

Example

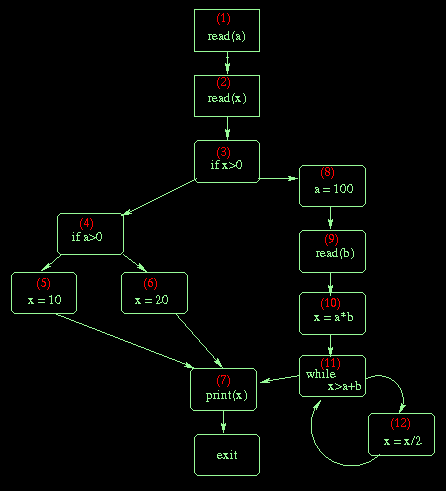
initial live ranges
-------------------
Def of a at node (1), {1, 2, 3, 4}
Def of x at node (2), {2, 3}
Def of x at node (5), {5, 7}
Def of x at node (6), {6, 7}
Def of a at node (8), {8, 9, 10, 11, 12}
Def of b at node (9), {9, 10, 11, 12}
Def of x at node (10), {7, 10, 11, 12}
Def of x at node (12), {7, 11, 12}

Final live ranges
-----------------
( <a>, {1, 2, 3, 4} )
( <x>, {2, 3} )
( <x>, {5, 6, 7, 10, 11, 12} )
( <a>, {8, 9, 10, 11, 12} )
( <b>, {9, 10, 11, 12} )

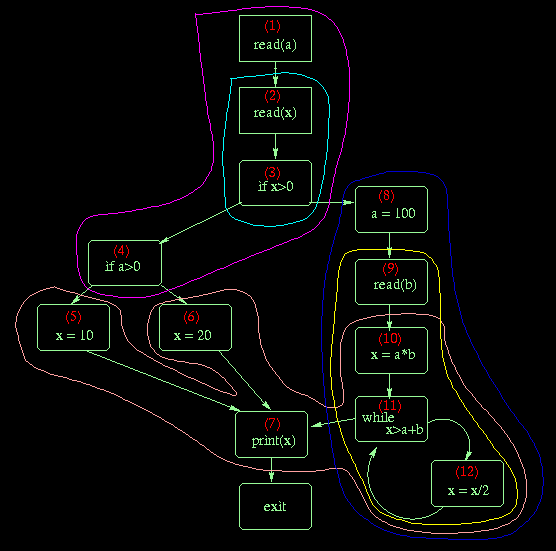
Step 2 - Build the Interference Graph

1 node for each live range
1 undirected edge n-m iff n intersect m != {}

Here is the graph for the live ranges shown above; the colors used above to encircle the live ranges are used to color the nodes of the interference graph.

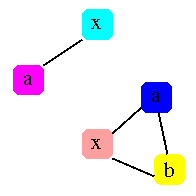
Step 3 - Color the Graph

given k, ( # of available registers )
  do: color graph with k colors
    such that no adjacent nodes have the same color

Note: This is an NP hard problem

It may be impossible to color the graph as specified above, and because it's an NP-hard problem, we can't tell (in a reasonable amount of time) whether or not it is possible. Therefore, we use the following heuristics:
1. Repeat: Remove "easy" nodes:
  - nodes with fewer than k neighbors are guaranteed to be colorable.
  - push these nodes onto a stack
  until there are no more easy nodes in the graph
2. If graph is non-empty after 1:
  - remove 1 node (push onto the stack)
  - to choose a node, take into account "cost", some function of: the number of definitions, the number of loops, loop nesting, and the number of unstacked neighbors the node has
  - go back to step 1
3. (Graph empty, all nodes on the stack)
  - pop each node n in turn
  - if non-stacked neighbors don't use all colors then color n with a free color.

In the running example, suppose we have two colors (R1 and R2). There are two "easy" nodes, the ones for x and a that are only connected to eachother (the magenta a and the light blue x). Those would be pushed onto the stack first.

The remaining nodes all have 2 incident edges, so we'd choose one of them to be pushed. Assume that we choose the node for a. Now the two remaining nodes both become "easy", and are pushed. At this point, the stack might look like:

     x {5, 6, 7, 10, 11, 12}  <-- top
     b {9, 10, 11, 12}
     a {8, 9, 10, 11, 12}
     x {2, 3}
     a {1, 2, 3, 4}

When the nodes are popped, they might be colored like this:

          Live Range             Color (register)
	  ==========		 ================

     x {5, 6, 7, 10, 11, 12}           R1
     b {9, 10, 11, 12}                 R2
     a {8, 9, 10, 11, 12}              -- no color --
     x {2, 3}                          R1
     a {1, 2, 3, 4}		       R2

Step 4 - Translate colors to registers

for each colored live range (x, S)
  for each CFG node n in S
  replace all instances of x in n
  with the appropriate register

Here's the final program with the colors converted to registers:

read(R2);
read(R1);
if (R1 > 0) {
    if (R2 > 0) R1 = 10;
    else (R1 = 20);
}
else {
    a = 100;
    read(R2);
    R1 = a * R2;
    while (R1 > A + R2) {
        R1 = R1 / 2;
    }
}
print(R1);

Summary: Register Allocation via Graph Coloring

Step 1 - compute live ranges
Step 2 - build interference graph
Step 3 - color the graph
Step 4 - convert colors to registers.

Register Allocation

Contents

Overview

Stack Model

Sethi-Ullman Register Allocation

Step 1 (Label each node with min # of registers)

Step 2 (generate code)

Semi-global register allocation

Global register allocation

Linear Scan

Overview

Linear Scan Algorithm

Graph Coloring

Step 1: compute live ranges

Step 2 - Build the Interference Graph

Step 3 - Color the Graph

Step 4 - Translate colors to registers

Summary: Register Allocation via Graph Coloring