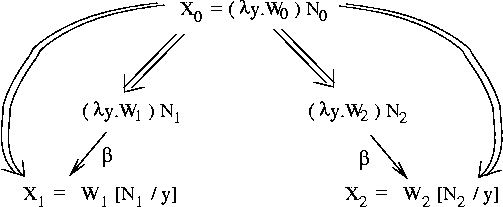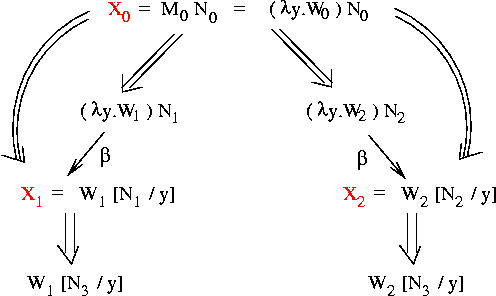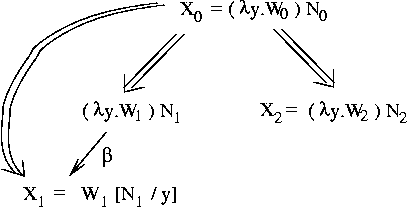Problems with the naive rewriting rule
Recall that the imprecise definition of rewriting an application (λx.M)N is "M with all occurrences of x replaced by N". However, there are two problems with this definition.
Problem #1: We don't, in general, want to replace all occurrences of x. To see why, consider the following (non-pure) lambda expression:
- (λx.(x + ((λx.x+1)3)))2
- (λx.x+1)3
- (λx.(x + 4))2
However, if we rewrite the outer application first, using the naive rewriting rule, here's what happens:
apply
/\
λ 2
/ \
x + +
/ \ / \
x apply => 2 apply => + => 5
/ \ (bad / \ / \
λ 3 application) λ 3 2 +
/ \ / \ / \
x + x + 2 1
/ \ / \
x 1 2 1
We get the wrong answer (5 instead of 6), because we replaced the
occurrence of x in the inner expression with the value supplied
as the parameter for the outer expression.
Problem #2: Consider the (pure) lambda expression
- ((λx.λy.x)y)z
- (λy.y)z
- z
To understand how to fix the first problem illustrated above, we first need to understand scoping, which involves the following terminology:
- Bound Variable: a variable that is associated with some lambda.
- Free Variable: a var that is not associated with any lambda.
λ
/ \
x /\
/ \
/ \
/..x...\
|
this x is bound
Here is a precise definition of free and bound variables:
- In the expression x, variable x is free (no variable is bound).
- In the expression λx.M, every x in M is bound; every variable other than x that is free in M is free in λx.M; every variable that is bound in M is bound in λx.M.
- In the expression MN:
- The free variables of MN are the union of two sets: the free variables of M, and the free variables of N.
- The bound variables of MN are also the union of two sets: the bound variables of M and the bound variables of N.
(λx.y)(λy.yx)
| ||
| |free
free |
bound
To solve problem #1 above,
given lambda expression
-
(λx.M)N
+----- M ---------+
| |
(λx. x + ((λx.x + 1)3)) 2
| |
| |
free bound
in M in M
=> 2 + ((λx.x + 1)3)
The issue behind problem #2 is that a variable y that is free in the
original argument to a lambda expression becomes bound after rewriting
(using that argument to replace all instances of the formal parameter),
because it is put into the scope of a lambda with a formal that happens
also to be named y:
((λx.λy.x)y)z
|
|
free, but gets bound after application
To solve problem #2, we use a technique called alpha-reduction. The basic idea is that formal parameter names are unimportant; so rename them as needed to avoid capture. Alpha-reduction is used to modify expressions of the form "λx.M". It renames all the occurrences of x that are free in M to some other variable z that does not occur in M (and then λx is changed to λz). For example, consider λx.λy.x+y (this is of the form λx.M). Variable z is not in M, so we can rename x to z; i.e.,
- λx.λy.x+y alpha-reduces to
λz.λy.z+y
alphaReduce(M: lambda-expression,
x: id,
z: id) {
// precondition: z does not occur in M
// postcondition: return M with all free occurrences of x replaced by z
case M of {
VAR(x): return VAR(z)
VAR(y): return VAR(y)
APPLY(e1, e2): return APPLY(alphaReduce(e1, x, z), alphaReduce(e2, x, z))
LAMBDA(x,e): return LAMBDA(x,e)
LAMBDA(y,e): return LAMBDA(y, alphaReduce(e, x, z))
}
}
Note: Another way to handle problem #2 is to use what's called de Bruijn notation, which uses integers instead of identifiers. That possibility is explored in the first homework assignment.
We are finally ready to give the precise definition of rewriting:
The left-hand side ((λx.M)N) is called the redex.
The right-hand side (M[N/x]) is called the contractum
and the notation means M with all free occurrences of x
replaced with N in a way that avoids capture.
We say that (λx.M)N beta-reduces to M with N substituted for x.
And here is pseudo code for substitution.
As discussed above, computing with lambda expressions involves
rewriting them using beta-reduction.
There is another operation, beta expansion that we can
also use.
By definition, lambda expression e1 beta-expands to e2 iff
e2 beta-reduces to e1.
So for example, the expression
A computation is finished when there are no more redexes (no more
applications of a function to an argument).
We say that a lambda expression without redexes is in normal form,
and that a lambda expression has a normal form iff there is some
sequence of beta-reductions and/or expansions that leads to a normal form.
This leads to some interesting questions about normal form:
Definition: An outermost redex is a redex that is not
contained inside another one.
(Similarly, an innermost redex is one that has no redexes
inside it.)
In terms of the abstract-syntax tree, an "apply" node represents an
outermost redex iff
For example:
To do a normal-order reduction, always choose the leftmost of
the outermost redexes (that's why normal-order reduction is also called
leftmost-outermost reduction).
Normal-order reduction is like call-by-name parameter passing, where you
evaluate an actual parameter only when the corresponding formal is used.
If the formal is not used, then you save the work of evaluating the actual.
The leftmost outermost redex cannot be part of an argument to another
redex; i.e., reducing it is like executing the function body, rather than
evaluating an actual parameter.
If it is a function that ignores its argument, then reducing that redex
can make other redexes (those that define the argument) "go away";
however, reducing an argument will never make the function "go away".
This is the intuition that explains why normal-order reduction will get
you to a normal form if one exists, even when other sequences of
reductions will not.
Fill in the incomplete abstract-syntax tree given above (to illustrate
"outermost" redexes) so that the resulting lambda expression has
a normal form and the only way to get there is by choosing the leftmost
outermost redex (instead of some other redex) at some point in the reduction.
You may be wondering whether it is a good idea always to use
normal-order reduction (NOR).
Unfortunately, the answer is no;
the problem is that NOR can be very inefficient.
The same issue arises with call-by-name parameter passing:
if there are many uses of a formal parameter in a function, and
you evaluate the corresponding actual each time the formal is used,
and evaluating the actual is expensive, then you would have been
better off simply evaluating the actual once.
This leads to the definition of another useful evaluation order:
leftmost innermost or applicative-order reduction (AOR).
For AOR we always choose the leftmost of the innermost redexes.
AOR corresponds to call-by-value parameter passing: all arguments are
evaluated (once) before the function is called (or, in terms of
lambda expressions, the arguments are reduced before applying the
function).
The advantage of AOR is efficiency: if the formal parameter appears many
times in the body of the function, then NOR will require that the
actual parameter be reduced many times while AOR will only require that
it be reduced once.
The disadvantage is that AOR may fail to terminate on a lambda expression
that has a normal form.
It is worth noting that, for programming languages, there is a solution
called call-by-need parameter passing that provides the best of
both worlds.
Call-by-need is like call-by-name in that an actual parameter is only
evaluated when the corresponding formal is used;
however, the difference is that when using call-by-need, the result
of the evaluation is saved and is then reused for each subsequent use
of the formal.
In the absence of side-effects (that cause different evaluations of the
actual to produce different values), call-by-name and call-by-need
are equivalent in terms of the values computed (though call-by-need
may be more efficient).
Define a lambda expression that can be reduced to normal form using
either NOR or AOR, but for which AOR is more efficient.
Now it's time for our first theorem: The Church-Rosser Theorem.
First, we need one new definition:
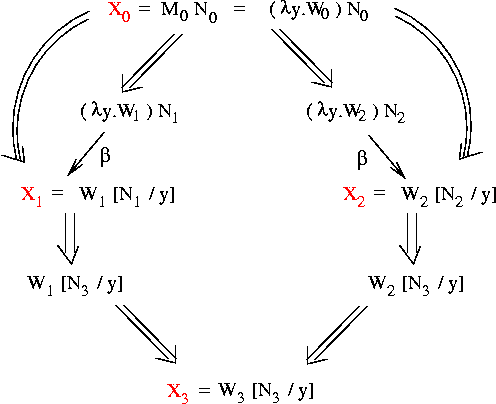
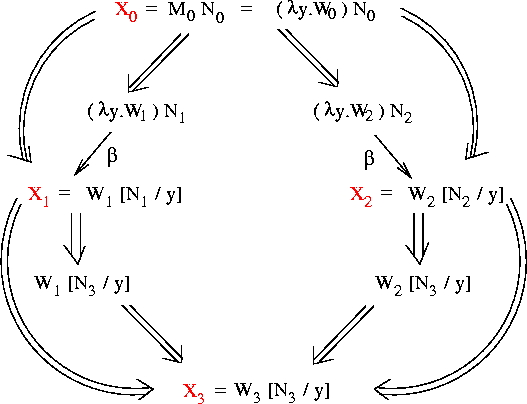
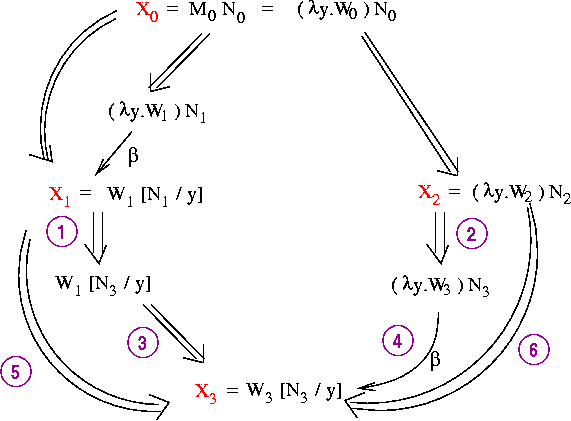
Theorem: if (X0 red X1) and (X0 red X2), then there is an X3
such that: (X1 red X3) and (X2 red X3).
Pictorially:
Corollaries: if X has normal form Y then
First we'll assume that the theorem is true, and prove the two corollaries;
then we'll prove the theorem.
To make things a bit simpler, we'll assume that we're using DeBruijn
notation; i.e., no alpha-reduction is needed.
To prove Corollary 1, note that "X has normal form Y" means that
we can get from X to Y using some sequence of interleaved beta-reductions
and beta-expansions.
Pictorially we have something like this:
We will prove Corollary 1 by induction on the number of changes of
direction in getting from X to Y.
Base cases
Now we're ready for the induction step:
Induction Hypothesis:
If X has normal form Y, and we can get from X to Y using a sequence
of beta-expansions and reductions that involve n changes of direction
(for n >= 1),
then we can get from X to Y using only beta-reductions.
Now we must show that (given the induction hypothesis)
Corollary 1 holds for n+1 changes of direction.
Here's a picture of an X and a Y such that n+1 changes of direction
are needed to get from X to Y:
Recall that Corollary 2 says that if lambda-term X has normal form Y then
Y is unique (up to alpha-reduction); i.e., X has no other normal form.
We can prove that by contradiction:
Assume that, in contradiction to the Corollary, Y and Z are two
different normal forms of X.
By Corollary 1, X reduces to both Y and Z:
Recall that the theorem is:
Where "red" means "zero or more beta-reductions" (since we're assuming
de Bruijn notation, and thus ignoring alph-reductions).
We'd like to prove the theorem by "filling in the diamond" from
X0 to X3; i.e., by showing that something like the following
situation must exist:
Unfortunately, this idea doesn't quite work; i.e., it is not
true in general that we can get to common term C in just one step from
A and one step from B.
Below is an example that illustrates this, using * to mean
a redex that reduces to y.
So to prove the Church-Rosser Theorem, we need a new definition:
Definition (the diamond property):
A relation ~~> on terms has the diamond property iff
Note:
To prove the Church-Rosser Theorem we will perform the following 3 tasks:
Finally, we'll prove that ⇒* (a sequence of zero or more walks)
has the diamond property, and we'll use that to "fill in the diamond"
and thus to prove the Church-Rosser Theorem.
Definition (walk):
A walk is a sequence of zero or more beta-reductions restricted as follows:
Here are some examples (again, * means a redex that reduces to y):
Here are two important insights about walks:
NOTE: We've now accomplished task (1) toward proving the Church-Rosser Theorem.
Task 2 involves proving that (X beta-reduce* Y) iff (X walk* Y).
The => direction is trivial; we must show that every sequence of
zero or more beta-reductions is also a sequence of walks.
Since each individual beta-reduction is a walk, we just let the
sequence of walks be exactly the sequence of beta-reductions.
The <= direction is easy, too.
Every walk is a sequence of zero or beta-reductions.
So every sequence of walks is a concatenation of sequences of beta-reductions,
which is itself a sequence of beta-reductions.
Beta-reduction
We use the following notation for beta-reduction;
(λx.M)N →β M[N/x]
substitute(M: lambda-expression,
x: id,
N: lambda-expression) {
// when substitute is first called, M is the body of a function of the form λx.M
case M of {
VAR(x): return N
VAR(y): return M
LAMBDA(x,e): return M // in this case, there are no free occurrences of
// x in M, so no substitutions can be done;
// note that this solves problem #1
LAMBDA(y,e):
if (y does not occur free in N)
then return LAMBDA(y,substitute(e,x,N)) // substitute N for x in the
// body of the lambda expression
else { // y does occur free in N; here we address problem #2
let y' be an identifier that is neither x nor y, and occurs in
neither N nor e;
let e' = alphaReduce(e,y,y');
return LAMBDA(y',substitute(e',x,N))
}
APPLY(e1,e2): return APPLY(substitute(e1,x,N), substitute(e2,x,N))
}
}
To illustrate beta-reduction, consider the previous example of problem #2.
Here are the beta-reduction steps:
((λx.λy.x)y)z
-> ((λy.x)[y/x])z // substitute y for x in the body of "λy.x"
-> ((λy'.x)[y/x])z // after alpha reduction
-> (λy'.y)z // first beta-reduction complete!
-> y[z/y'] // substitute z for y' in "y"
-> y // second beta-reduction complete!
Note that the term "beta-reduction" is perhaps misleading, since
doing beta-reduction does not always produce a smaller lambda expression.
In fact, a beta-reduction can:
the length of a lambda expression.
Below are some examples.
In the first example, the result of the beta-reduction is the
same as the input (so the size doesn't change);
in the second example, the lambda expression gets longer and longer;
and in the third example, the result first gets longer, and then
gets shorter.
Normal Form
xy
beta-expands to each of the following:
(λa.a)xy
(λa.xy)(λz.z)
(λa.ay)x
A: No, e.g.: (λz.zz)(λz.zz). Note that this should not be
surprising, since lambda calculus is equivalent to Turing
machines, and we know that a Turing machine may fail to halt
(similarly, a program may go into an infinite loop or an infinite
recursion).
A: Beta-reductions are good enough (this is a corollary
to the Church-Rosser theorem, coming up soon!)
A: No. Consider the following lambda expression:
(λx.λy.y)((λz.zz)(λz.zz))
This lambda expression contains two redexes: the first is the
whole expression (the application of (λx.λy.y) to
its argument); the second is the argument itself:
((λz.zz)(λz.zz)).
The second redex is the one we used above to illustrate a
lambda expression with no normal form; each time you beta-reduce
it, you get the same expression back. Clearly, if we keep
choosing that redex to reduce we're never going to find a normal
form for the whole expression. However, if we reduce the first
redex we get: λy.y, which is in normal form.
Therefore, the sequence of choices that we make can
determine whether or not we get to a normal form.
A: Yes! It is called leftmost-outermost or
normal-order-reduction (NOR), and we'll define it below.
Normal-Order and Applicative-Order Reduction
apply <-- not a redex
/ \
an outermost redex --> apply apply <-- another outermost redex
/ \ / \
λ ... λ apply <-- redex, but not outermost
/ \ / \ / \
... ... ... ... λ ...
The Church-Rosser Theorem
A red B means there is a sequence of zero or more alpha-
and/or B-reductions that transform A into B.
X0
/ \
/ \
/ \
v v
X1 X2
\ /
\ /
\ /
\ /
v v
X3
where the arrows represent sequences of zero or more alpha- and/or
beta-reductions.
Proof of Corollary 1
^
/
^ /
/ \ / ...... \
/ \ / \
X v \
v
Y
where the upward-pointing arrows represent a sequence of beta-expansions,
and the downward-pointing arrows represent a sequence of beta-reductions.
Note that we cannot end with an expansion, since Y is in normal
form.
X
\
\
v
Y
i.e., we got from X to Y using zero or more beta-reductions, so
we're done.
W
^ \
/ \
/ \
/ v
X Y
i.e., we first use some beta-expansions to get from X to some lambda
expression W, then use some beta-reductions to get from W to Y.
Because every beta-expansion is the inverse of a beta-reduction,
this means that we can get from W to X (as well as from W to Y)
using a sequence of beta-reductions;
i.e., we have the following picture:
W
/ \
/ \
/ \
v v
X Y
The Church-Rosser Theorem guarantees that there's a Z such that both
X and Y reduce to Z:
W
/ \
/ \
v v
X Y
\ /
\ /
v v
Z
Since Y is (by assumption) in normal form, it must be that Y = Z, and
our picture really looks like this:
W
/ \
/ |
v |
X |
\ |
\ /
v v
Y
which means that X reduces to Y without any expansions.
W
^ \ ^ \ ^ \
/ \ / \ / \
/ \ / \ /
/ v / v / v
X ... ... Y
<--1 change --> <-- n changes of direction -->
Note that there is some lambda expression W (shown in the picture
above) such that:
By the induction hypothesis, point 2 above means that we can get
from W to Y using only beta reductions:
W
\
\
v
Y
Combining this with point 1 we have:
W
^ \
/ \
/ \
/ v
X Y
In other words, we can get from X to W using only beta-expansions, and
from W to Y using only beta-reductions.
Using the same reasoning that we used above to prove the second base
case, we conclude that we can get from X to Y using only beta-reductions.
Proof of Corollary 2
X
/ \
/ \
/ \
v v
Y Z
By the Church-Rosser Theorem, this means there is W, such that:
X
/ \
/ \
v v
Y Z
\ /
\ /
v v
W
However, since by assumption Y and Z are already in normal form,
there are no reductions to be done; thus, Y = W = Z, and X does
not have two distinct normal forms.
Proof of the Church-Rosser Theorem
if (X0 red X1) and (X0 red X2), then there is an X3
such that: (X1 red X3) and (X2 red X3).
X0
/ \
W1 Z1
/ \ / \
W2 A X2
/ \ / \ /
X1 B C
\ / \ /
D E
\ /
F = X3
In other words, we'd like to show that for every lambda term, if you
can take two different "steps" (can do two different beta-reductions)
to terms A and B, then you can come back to a common term C by doing
one beta-reduction from A, and one from B.
If we could show that, then we'd have the desired X3 by construction
as shown in the picture above.
X0 = (λx.xx)(*)
/ \
/ \
(**) (λx.xx)y
\ /
\ /
\ /
(y*) or (*y) /
\ /
\ /
(yy)
Note that there are two redexes in the initial term X0: * itself,
and the one in which * is the argument to a lambda-term.
So we can take two different "steps" from X0, arriving either at
(**) or at (λx.xx)y.
While we can come back to a common term, (yy), from both
of those, it requires two steps from (**).
( X0 ~~> X1) and ( X0 ~~> X2) implies there is an X3
such that ( X1 ~~> X3 ) and ( X2 ~~> X3 )
The three tasks
Task 1
If the ith reduction in the sequence reduces a redex r,
then no later reduction in the sequence can reduce an instance of
a redex that was inside r;
i.e., reductions must be done bottom-up
in the abstract-syntax tree.
(λx.xx)(*)
|
|
v
(λx.xx)y
|
|
v
yy
This entire reduction sequence (2 beta-reductions) is a walk because
the inner redex is reduced first.
Here's what the reductions look like using the abstract-syntax tree:
apply apply apply
/ \ / \ / \
λ * λ y y y
/ \ --> / \ -->
x apply x apply
/ \ / \
x x x x
However, consider this sequence of beta-reductions (starting with the same
initial term), first showing the lambda terms, then the abstract-syntax
trees:
(λx.xx)(*)
|
|
v
(**)
|
|
v
(y*)
|
|
v
(yy)
apply apply apply apply
/ \ / \ / \ / \
λ * * * y * y y
/ \ --> --> -->
x apply
/ \
x x
==> =======================>
this step is a these two steps constitute a walk
walk
Although as noted above, the first beta-reduction is a walk, and the
second and third together are also a walk,
the sequence of three reductions is not a walk because once the
root "apply" is chosen to be reduced (which happens as the first reduction),
no apply in the tree can be reduced as part of the same walk (so the reductions
of the two "*" terms are illegal).
Task 2