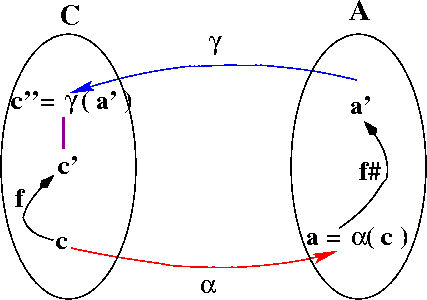
Relationship between standard and abstract interpretations.
The abstract interpretation defined above for the "rule-of-signs" example was very simple and intuitive. Assuming that I didn't make any typographical errors when typing in the two tables, it shouldn't be hard to convince yourself that the abstract semantics is consistent with the standard (concrete) semantics. However, to be sure that this consistency holds, we must do the following:
- Define two partially-ordered sets (posets) C and A. The elements of C are all non-empty sets of values from the concrete domain (i.e., sets of integers). The elements of A are the values from the abstract domain (i.e., neg, zero, pos, and num).
- Define an abstraction function α that maps non-empty sets of integer values to Sign values (i.e., α is of type C → A).
- Define a concretization function γ that maps Sign values to non-empty sets of integer values (i.e., γ is of type A → C).
- Show that α and γ form a Galois connection (defined below).
- For each possible form of expression exp, show that
- { E[[exp]] } ⊆ γ(Eabs[[exp]])
1. Abstraction function α.
For the rule-of-signs example, the abstraction function is defined as follows:
| α({0}) = | zero |
| α(S) = | if all values in S are greater than 0 then pos |
| else if all values in S are less than 0 then neg | |
| else num |
2. Concretization function γ.
And the concretization function is defined as follows:
| γ(zero) = {0} |
| γ(pos) = {all positive ints} |
| γ(neg) = {all negative ints} |
| γ(num) = Int (i.e., all ints) |
3. Galois Connection.
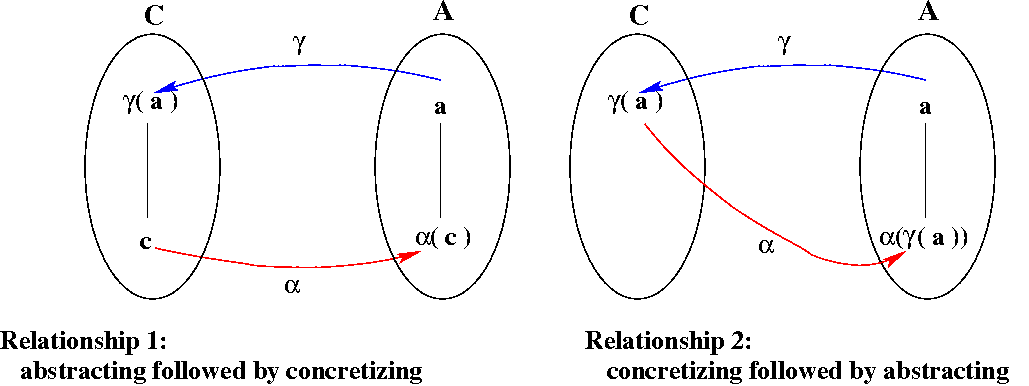
A Galois connection is a pair of functions, α and γ between two partially ordered sets (C, ⊆) and (A, ≤), such that both of the following hold.
- ∀ a ∈ A, c ∈ C: α(c) ≤ a iff c ⊆ γ(a)
- ∀ a ∈ A: α(γ(a)) ≤ a
Here are the two relationships we need, presented pictorially:
For our example, poset A is the set containing the four elements of Sign (with num as the top element, and no ordering relationship among the other three elements), and poset C is the set of all sets of integers, ordered by subset. Here is a picture with all of A and some of C. Some of the alpha mapping (the abstraction function) is shown using red arrows, and some of the gamma mapping (the concretization function) is shown using blue arrows.
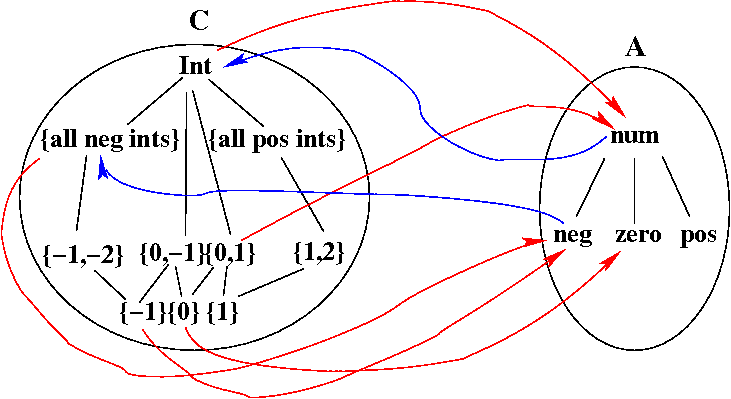
Question 1: Fill in the remaining alpha and gamma edges in the figure above.
Question 2: Show that alpha and gamma do form a Galois connection.
4. Safety. Our final obligation in proving that our rule-of-signs abstract interpretation is consistent with the standard semantics is to prove that, for every expression exp,
- { E[[exp]] } ⊆ γ(Eabs[[exp]])
Base case: exp is literal k. This case has three parts (based on the definition of Eabs):
- k < 0: In this case,
E[[k]] = k // def of E Eabs[[k]] = neg // def of Eabs γ(neg) = {all negative ints} // def of γ - k = 0: In this case,
E[[k]] = 0 // def of E Eabs[[k]] = zero // def of Eabs γ(zero) = {0} // def of γ - k > 0: In this case,
E[[k]] = k // def of E Eabs[[k]] = pos // def of Eabs γ(pos) = {all positive ints} // def of γ
Inductive Step
The inductive step is quite tedious. There are two cases (one for addition and one for multiplication), and each has 16 sub-cases (for all possible combinations of the signs of the two sub-expressions). Here is one example to show the flavor of the proof.
Inductive case 1: exp is e1 + e2.
| RHS: | γ(Eabs[[e1 + e2]]) | |
| = γ(Eabs[[e1]] ⊕ Eabs[[e2]]) | // def of Eabs |
sub-case 1: both Eabs[[e1]] and Eabs[[e2]] are neg.
| = γ(neg ⊕ neg) | ||
| = γ(neg) | // def of ⊕ | |
| = { all negative ints } | // def of γ | |
| LHS: | E[[e1 + e2]] | |
| = E[[e1]] + E[[e2]] | // def of E |
By the induction hypothesis, E[[e1]] is a subset of γ(Eabs[[e1]]), which is γ(neg), which is the set of all negative ints. The same applies to E[[e1]]. Thus, the LHS is the sum of two negative ints, which is a negative int, which is certainly a subset of { all negative ints } (the final value for the RHS).
In what way does proving that
- { E[[exp]] } ⊆ γ(Eabs[[exp]])
Standard and Collecting Semantics for CFGs
For the simple rule-of-signs example, we were able to define an abstract interpretation as a variation on the standard denotational semantics. For more realistic static-analysis problems, however, the standard denotational semantics is usually not a good place to start. This is because we usually want the results of static analysis to tell us what holds at each point in the program, and program points are usually defined to be the nodes of the program's control-flow graph (CFG). For example, for constant propagation we want to know, for each CFG node, which variables are guaranteed to have constant values when execution reaches that node. Therefore, it is better to start with a (standard) semantics defined in terms of a CFG.
There are various ways to define a CFG semantics.
The most straightforward is to define what is called an
operational semantics;
think of it as an interpreter whose input is the entry node of a CFG
plus an initial state (a mapping from variables to values),
and whose output is the program's final state.
We'll define the standard sementics in terms of
transfer functions, one for each CFG node.
These are (semantic) functions whose inputs are states and whose
outputs are pairs that include both an output state and
the CFG node that is the appropriate successor.
A node's transfer function captures the execution semantics
of that node and specifies the next node to be executed.
For example, consider the CFG shown below (with labels on the nodes).
For this example, the transfer function for node 2 would be defined
as follows:
Here's a (recursive) definition of the interpreter (the operational
semantics).
We use fn to mean the transfer function defined for
CFG node n.
Because this definition is recursive, we need to use the usual trick of
abstracting on the function and defining the operational semantics
as the least fixed point of that abstraction:
While the operational semantics discussed above is defined in terms of
the program's CFG, it has two properties that are undesirable
as the basis for an abstract interpretation:
We will define a collecting semantics that maps CFG nodes to sets
of states;
i.e., for each CFG node n, the collecting semantics tells us what
states can arise just before n is executed.
The "approximate semantics" that we define using abstract interpretation
will compute, for each CFG node, (a finite representation of) a superset of
the set of states computed for that node by the collecting semantics.
By showing that our abstract interpretation really does compute
a superset of the possible states that can arise at each CFG node,
we show that it is consistent with the program's actual semantics.
Because the collecting semantics involves sets of states, we need to
define transfer functions whose inputs and outputs are sets of states.
We'll define one function fn→m for each CFG edge
n→m.
That transfer function will be defined in terms of the (original) transfer
function fn defined for the CFG node n:
For example, the transfer function for edge 2→3 of the example CFG
given above would be defined as follows:
What is the transfer function (for the collecting semantics)
for edge 4→5 of the example CFG?
Our collecting semantics will be of type
CFG-node → set-of-states.
The (recursive) definition is given below.
It defines the set of states that holds just before node n to be
the union of the sets of states produced by applying
the transfer functions of all of n's in-edges
to the sets of states that hold just before the sources of those
in-edges execute.
And here's the non-recursive definition:
The values computed for iterations 9 and 10 are the same, so line 9
of the table defines function coll.
Standard Semantics
+----------+
| 1: start |
+----------+
|
v
+----------+
| 2: a = 1 |
+----------+
|
v
+----------+
| 3: b = 1 |
+----------+
|
v
+----------+ F +------------+ +---------+
+---> | 4: a < 3 |---->| 6: c = a+b |---->| 7: exit |
| +----------+ +------------+ +---------+
| |
| T |
| v
| +------------+
| | 5: a = a+b |
| +------------+
| |
| |
+-----------+
λs.(s[a ← 1], 3)
where s[a ← 1] means "a new state that is the same as s except that
it maps variable a to 1."
For node 4, the transfer function would be
λs.(if lookup(s, a) < 3 then (s, 5) else (s, 6))
In this case, the output state is the same as the input state;
the successor node depends on whether variable a is less than 3
in the current (input) state.
interp = λs.λn.
if isExitNode(n) then s
else let (s', n') = fn(s) in interp s' n'
semantics = fix(λF.λs.λn.
if isExitNode(n) then s
else let (s', n') = fn(s) in F s' n')
Collecting Semantics
The advantage of abstract interpretation compared to the kind
of dataflow analysis we studied in CS 701 is that it provides a
guarantee about the relationship between the program's semantics
and the analysis results.
To obtain that advantage, we need a semantics that includes information
about the set of states that can arise at each CFG node given any possible
initial state.
That kind of semantics is called a collecting semantics.
fn→m = λS.{s' | s∈S and fn(s) = (s', m)}
λS.{s[a ← 1] | s ∈ S}
.
recColl = λn.
if isEnterNode(n) then { all states }
else let P = preds(n) in ∪p ∈ P fp→n(recColl(p))
For our example program, we can actually find coll
by iterating up from bottom.
The elements of concrete poset C are sets of states (each with a value
for variables a, b, and c) and the ordering is subset.
This means that the bottom element of the poset is the empty set,
and the bottom function is the one that ignores its input and returns
the empty set.
Below is a table that shows the computation of coll.
We use the notation [ v1 v2 v3 ]
to mean a state in which a=v1, b=v2, and c=v3.
A tuple with a star, e.g., [1 * *], represents an infinite
set of states, including all possible values in place of the star
(so [ * * * ] represents all states, and [1 * *] represents all
states in which the only constraint is that a=1).
coll = fix(λF.λn.
if isEnterNode(n) then { all states }
else let P = preds(n) in ∪p ∈ P fp→n(F(p))