Execution Recovery Examples and Formulations
This page contains full formulations and more complete examples for the paper ‘‘Recovering Execution Data from Incomplete Observations,’’ published in the 13th International Workshop on Dynamic Analysis (WODA 2015).
Example Problem
The example problem (from the WODA paper) is as follows. First, we are given the following control-flow graph (CFG):
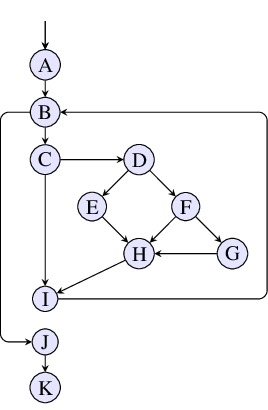 |
The remainder of our failure report is as follows:
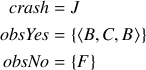
The goal of problem is to compute three sets: 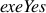 (containing
those nodes that occur on all paths through our CFG consistent with the failure
report),
(containing
those nodes that occur on all paths through our CFG consistent with the failure
report), 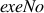 (containing those nodes that occur on no paths
matching the failure report), and
(containing those nodes that occur on no paths
matching the failure report), and 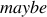 (containing those nodes that
occur on some but not all such paths). The following two sections provide the
full formulations to solving this problem that we describe in the
WODA paper.
(containing those nodes that
occur on some but not all such paths). The following two sections provide the
full formulations to solving this problem that we describe in the
WODA paper.
Finite-State Automata
This section provides the full collection of automata used for Section 2.1 of the paper.
Automata for 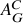
The first collection of automata encode constraints from the failure report
example from the paper. The
intersection of these automata forms 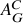 , an automaton that accepts only
strings corresponding to executions that match the provided failure report.
, an automaton that accepts only
strings corresponding to executions that match the provided failure report.
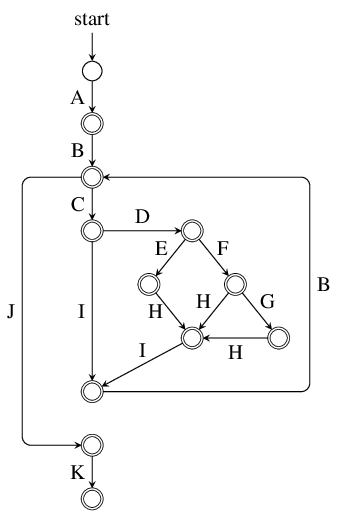 |
This first automaton is a direct encoding of our example Control-Flow Graph (CFG). Note that each CFG edge contributes one transition to the automaton, labeled with the target node's symbol.
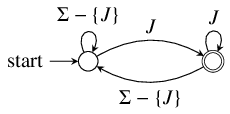 |
This second automaton encodes the crashing requirement. Specifically, it forces
accepted executions to end with CFG node 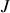 .
.
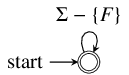 |
The third automaton encodes the  constraints. That is, it
forces accepted executions to not contain CFG nodes in
constraints. That is, it
forces accepted executions to not contain CFG nodes in 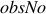 . In
this case, it ensures that no matched execution contains CFG node
. In
this case, it ensures that no matched execution contains CFG node 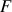 .
.
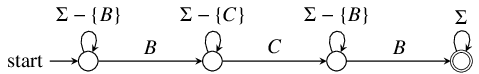 |
The final automaton encodes an 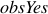 constraint. For our example
from the paper, there is only one such constraint. However, in the general
case, we would require one
constraint. For our example
from the paper, there is only one such constraint. However, in the general
case, we would require one 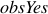 automaton for each vector contained
in
automaton for each vector contained
in 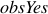 . In this case, we are encoding the constraint that all
matched executions must pass through CFG node
. In this case, we are encoding the constraint that all
matched executions must pass through CFG node 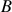 , followed by CFG node
, followed by CFG node 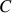 ,
followed by another occurrence of
,
followed by another occurrence of 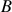 .
.
Probes to compute exeYes, exeNo, and maybe
To actually compute 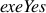 ,
, 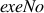 , and
, and 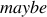 ,
we first create two automata for each node in our control-flow graph,
,
we first create two automata for each node in our control-flow graph, 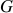 .
Checking the intersection of each automaton (independently) with
.
Checking the intersection of each automaton (independently) with 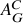 for
emptiness indicates whether the respective node is possible and/or
necessary. Here, we give the automata corresponding to probes for node
for
emptiness indicates whether the respective node is possible and/or
necessary. Here, we give the automata corresponding to probes for node 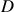 .
.
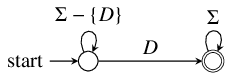 |
The first, 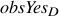 corresponds to the
corresponds to the 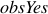 automaton
for the single-element
automaton
for the single-element 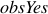 vector,
vector, 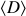 . If
. If
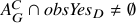 , then
, then 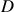 is possible.
is possible.
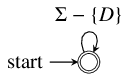 |
The second automaton, 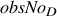 corresponds to the automaton for
corresponds to the automaton for
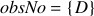 . If
. If
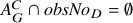 , then
, then 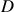 is necessary.
is necessary.
If a node,  is necessary, then
is necessary, then 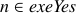 . If
. If  is not
possible, then
is not
possible, then 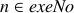 . Otherwise,
. Otherwise, 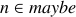 .
.
Answer-Set Programming
This section provides the full formulations for the logic programs used in Section 2.2 of the paper.
Failure Report Constraints
The failure report example described in the paper is here encoded in ASP format:
% CFG representation entry(a). node(a). node(b). node(c). node(d). node(e). node(f). node(g). node(h). node(i). node(j). node(k). edge(a, b). edge(b, c). edge(b, j). edge(c, d). edge(c, i). edge(d, e). edge(d, f). edge(e, h). edge(f, g). edge(f, h). edge(g, h). edge(h, i). edge(i, b). edge(j, k). % Observations crash(j). anyObsYes(b). anyObsYes(c). order(b, c). order(c, b). obsNo(f).
Background Constraints
The base encoding of the failure report consists of several rules
which specify how paths through the described graph function. To
do so, we introduce the concept of 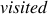 (which in
the encoding means any node which is visited by a possible path
of execution) and
(which in
the encoding means any node which is visited by a possible path
of execution) and 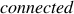 (here meaning that two nodes
are connected during a possible path of execution). These concepts
are encoded as follows:
(here meaning that two nodes
are connected during a possible path of execution). These concepts
are encoded as follows:
0 { visited(X) } 1 :- node(X).
visited(X) :- entry(X).
visited(X) :- crash(X).
-visited(X) :- obsNo(X).
visited(X) :- anyObsYes(X).
Roughly, any node can potentially be 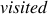 ; the
entry and crash nodes (as well as any in
; the
entry and crash nodes (as well as any in 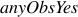 )
are, by definiton,
)
are, by definiton, 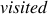 . Any node observed to,
specifically, not be visited (i.e., those in
. Any node observed to,
specifically, not be visited (i.e., those in 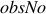 )
are explicitly not
)
are explicitly not 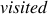 .
.
connected(X, X) :- visited(X). connected(X, Z) :- visited(X), edge(X, Y), connected(Y, Z).
A node is 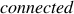 to itself if (and only if) it is
to itself if (and only if) it is
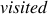 ; as well, inductively, a node is
; as well, inductively, a node is 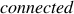 to another node if it is both
to another node if it is both 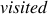 and has an edge to
another node which is
and has an edge to
another node which is 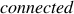 to the specified node.
to the specified node.
Probes to compute exeYes, exeNo, and maybe
To actually compute 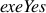 ,
, 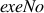 , and
, and 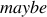 ,
we conjoin our complete set of constraints from a failure report with two
probes. This section describes that process, and what SAT and UNSAT mean in
each context.
,
we conjoin our complete set of constraints from a failure report with two
probes. This section describes that process, and what SAT and UNSAT mean in
each context.
exeYes
To define 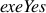 in our ASP encoding, we first define
a new concept,
in our ASP encoding, we first define
a new concept, 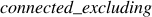 , which tests if two
nodes are
, which tests if two
nodes are 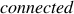 without the path of execution
passing through a specific third node.
without the path of execution
passing through a specific third node.
connected_excluding(X, Y, E) :- node(E), edge(X, Y), E != Y, E != X, not obsNo(Y). connected_excluding(X, Z, E) :- connected_excluding(X, Y, E), connected_excluding(Y, Z, E). connected_excluding(X, X, E) :- node(E), node(X), X != E.
With this concept defined, defining 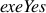 within ASP
becomes straightforward:
within ASP
becomes straightforward:
exeYes(X) :- crash(X). exeYes(X) :- entry(X). exeYes(X) :- obsYes(X).
The crash node, entry node, and any explicitly observed nodes are
contained in 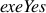 .
.
exeYes(X) :- exeYes(O), crash(C), node(X), not connected_excluding(O, C, X). exeYes(X) :- entry(E), exeYes(O), node(X), not connected_excluding(E, O, X).
All possible paths of execution through the program must start at the entry node and end at the crash node. Any additional nodes we know to have executed–whether through explicit observation or deduction–must then have a path both from the entry and to the crash. As such, any nodes that such a path must pass through are also known to have been executed.
The known ordering of nodes during a path also figure in to the encoding:
exeYes(X) :- order(Y, Z), node(X), not connected_excluding(Y, Z, X). exeYes(X) :- node(X), order(A, B), order(C, D), A != C, not connected_excluding(B, C, X), not connected_excluding(D, A, X).
Roughly, any node that must be executed when two nodes known to
have been executed in a specific order are in 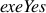 , as
well as any which must be executed to connect multiple ordered
nodes together.
, as
well as any which must be executed to connect multiple ordered
nodes together.
exeNo
The calculation of membership of 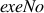 is somewhat simpler:
is somewhat simpler:
pospair_from(X, O) :- connected(O, X), connected(X, C), crash(C), exeYes(O). pospair_to(X, O) :- entry(E), connected(E, X), connected(X, O), exeYes(O). exeNo(X) :- node(X), exeYes(O), not pospair_to(X, O), not pospair_from(X, O).
If, for any node known to be executed, we cannot find a path from the entry to that node through a specified node and we cannot find a path from the known-executed node through the specified node to the crash, that specified node cannot have been executed.
maybe
If we know 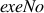 and
and 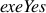 , then
, then 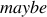 is a simple choice of “none of the above”:
is a simple choice of “none of the above”:
maybe(X) :- node(X), not exeNo(X), not exeYes(X).
Probes
The ASP encoding of the failure report allows easy direct queries of the
membership of the defined sets by adding the membership of a node to a
proposed set as a fact along with the encoding of the observations. For
example, if we wish to directly test 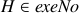 , we
can add exeNo(H) to the input to the ASP grounder, and then determine
its truth by the SAT solver's output: a result of SAT tells us our
assertion was true with UNSAT proving our assertion false.
, we
can add exeNo(H) to the input to the ASP grounder, and then determine
its truth by the SAT solver's output: a result of SAT tells us our
assertion was true with UNSAT proving our assertion false.