Symbolic Automata
Classic automata theory builds on the assumption that the alphabet is finite.
Unfortunately, practical applications such as XML processing and program trace analysis use values for individual symbols
that are typically drawn from an infinite domain.
Even when the alphabet is finite, classic automata may sometimes be a bad choice: for example a deterministic finite automata
modelling a language over the UTF16 alphabet requires 2^16 transitions out of each state!
What are Symbolic Automata and Transducers?
Symbolic Finite Automata (SFAs) are finite state automata in which the alphabet is given by a Boolean algebra that
may have an infinite domain, and transitions are labeled with first-order predicates over such algebra.
For example a symbolic automaton (shown on the right) can define the following property:
|
OddG1 = {l | l is a list of odd numbers with length greater than 1}
|
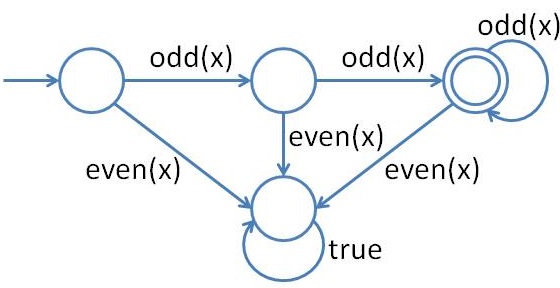
|
In order for SFAs to be closed under Boolean operations and preserve decidability of equivalence,
it should be decidable to check whether predicates in the algebra are satisfiable.
In the example above predicates are expressed in Presburger arithmetic which is
indeed a decidable theory closed under Boolean operations.
Symbolic Finite Transducers (SFTs) extend SFAs to output lists. In a SFT
transitions, upon reading an input symbol, can compute an output that
is expressed as a function of the input being read.
Such a function has to belong to the underlying alphabet theory.
Many variants of SFAs and SFTs have been proposed, and this page tries to keep up with such extensions.
How do they relate to classic Automata?
Symbolic Finite Automata are strictly more expressive than deterministic finite automata.
Despite this fact,
Symbolic Finite Automata are closed under Boolean operations and admit decidable equivalence.
In general for large alphabets Symbolic Automata outperforms their classic counterpart.
In fact even complex regular expressions over UTF16 can be analyzed using symbolic automata.
References
We recommend reading
this paper to get started.
You can also watch this
talk.
The purpose of this page is to keep track of the latest results related to this topic. Email me (loris at cs.wisc.edu) with comments and/or suggested additions.
Decision Problems and Closure Properties
-
Symbolic Finite State Transducers:
Algorithms and Applications
[ pdf ],
N, Bjorner, P. Hooimeijer, B. Livshits, D. Molnar, M. Veanes,
POPL12
-
Minimization of Symbolic Automata
[ pdf ],
L. D'Antoni, M. Veanes,
POPL14
-
A Symbolic Decision Procedure for
Symbolic Alternating Finite Automata
[ pdf ],
L. D'Antoni, Z. Kincaid, F. Wang,
MFPS XXXIII
-
Forward Bisimulations for Nondeterministic Symbolic Finite Automata
[ pdf ],
L. D'Antoni, M. Veanes,
TACAS 17
-
The power of symbolic
automata and transducers
[ pdf ],
L. D'Antoni, M. Veanes,
TACAS 17
-
Theoretical Aspects of Symbolic Automata
[ pdf ],
H. Tamm, M. Veanes,
SOFSEM 18
Extensions to Trees and Nested Words
-
Symbolic Tree Transducers
[ pdf ],
M. Veanes, N. Bjorner,
PSI11,
WARNING! Theorem 1 is wrong.
-
Forward and Backward Application of
Symbolic Tree Transducers
[ pdf ],
Z. Fulop, H. Vogler,
Acta Informatica
-
Fast: A Transducer-Based Language for Tree Manipulation
[ pdf ],
L. D'Antoni, M. Veanes, B. Livshits, D. Molnar
TOPLAS
-
Symbolic Visibyly Pushdown Automata
[ pdf ],
L. D'Antoni, R. Alur,
CAV14
-
Minimization of Symbolic Tree Automata
[ pdf ],
L. D'Antoni, M. Veanes,
LICS16
Other Extensions
-
Extended Symbolic Finite Automata and Transducers
[ link ],
L. D'Antoni, and M. Veanes,
FMSD 15
-
A Theory of Synchronous Relational Interfaces (Section 6)
[ pdf ],
S. Tripakis, B. Lickly, T. A. Henzinger, E. A. Lee,
TOPLAS11
-
Monadic second-order logic on finite sequences [ pdf ]
L. D'Antoni, M. Veanes
POPL 17
-
Abstract Symbolic Automata: Mixed syntactic/semantic similarity analysis of executables
M. Dalla Preda, R. Giacobazzi, A. Lakhotia, I. Mastroieni
POPL 17
-
Symbolic Register Automata
[ pdf ]
L. D'Antoni, T. Ferreira, M. Sammartino, A. Silva
CAV 19
Learning
-
Learning Regular Languages over Large Alphabets
[ pdf ],
O. Maler, I. E. Mens,
TACAS14
-
Learning Symbolic Automata,
[ pdf ],
S. Drews and L. D'Antoni,
TACAS 17
-
The Learnability of Symbolic Automata,
[ pdf ],
G. Argyros and L. D'Antoni,
CAV 18
-
Verifying Sanitizer Correctness through Black-Box Learning: A Symbolic Finite Transducer Approach,
[ pdf ],
S. Lathouwers, M. Everts, M. Huisman,
FORSE 20
Applications
-
Symbolic Automata Constraint Solving [ pdf ],
M. Veanes, N. Bjorner, L. de Moura,
LPAR10
-
From Sequential Extended Regular Expressions to NFA with Symbolic Labels
[ pdf ],
Alessandro Cimatti, Sergio Mover, Marco Roveri, Stefano Tonetta,
CIAA10
-
Symbolic Automata: The Toolkit
[ pdf ],
M. Veanes, N. Bjorner,
TACAS11
-
Fast and Precise Sanitizer Analysis with BEK [ pdf ],
P. Hooimeijer, B. Livshits, D. Molnar, P. Saxena, M. Veanes,
USENIX Security'11
-
Static Analysis of String Encoders and Decoders
[ pdf ],
L. D'Antoni, M. Veanes,,
VMCAI13
-
Applications of Symbolic Finite Automata
[ pdf ],
M. Veanes,
CIAA13
-
Data-Parallel String-Manipulating Programs
[ pdf ],
M. Veanes, D. Molnar, T. Mytkowicz, B. Livshits
POPL 2015
-
DReX: A Declarative Language for Efficiently Evaluating
Regular String Transformations
[ pdf ],
R. Alur, L. D'Antoni, M. Raghothaman,
POPL 2015
-
Back in Black: Towards Formal, Black Box Analysis of Sanitizers and Filters
[ web ],
G. Argyros, I. Stais, A. Kiayias, A. Keromytis,
S&P 2016
-
SFADiff: Automated Evasion Attacks and Fingerprinting Using Black-box Differential Automata Learning
[ web ],
G. Argyros, I. Stais, S. Jana, A. Keromytis, A. Kiayias,
CCS 2016
-
Automatic Program Inversion using Symbolic Transducers
[ pdf ],
Q. Hu and L. D'Antoni,
PLDI 2017
-
An Algebraic Framework for Runtime Verification
[ web ],
S. Jaksic, E. Bartocci, R. Grosu, D. Nickovic,
TCAD 2018
-
Aragog: Scalable Runtime Verification of Shardable Networked Systems
[ web ],
N. Yassen, B. Arzani, R. Beckett, S. Ciraci, B. Liu,
OSDI 2020
Tools based on Symbolic Automata and Transducers
-
symbolicautomata: a Java symbolic automata library. L. D'Antoni
-
Microsoft Automata Library: a library for symbolic automata.
M. Veanes, N. Bjorner
-
Rex: a command line tool that generates matching strings for .NET regexes. M. Veanes
-
Bek: a transducer-based language for
string manipulation. M. Veanes, P. Hooimeijer, B. Livshits, D. Molnar, N. Bjorner
-
Bex: a transducer-based language for analysis
of string encoders and decoders. L. D'Antoni, M. Veanes
-
Fast: a transducer-based Language for analysis of tree manipulating
programs. L. D'Antoni, M. Veanes, B. Livshits, D. Molnar
-
Mona: A solver for Monadic Second-Order logic. Aarhus University
