Finding Roots

Contents

Problem statement

Find root of

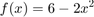
clear

% Define a function handle representing the function
f = @(x)6 - 2*x.^2;

% First plot the function
xx = -3 : 0.01 : 3;
yy = f(xx);
ymin = -7;
ymax = 7;
xmin = -3;
xmax = 3;
plot(xx, yy, 'b', [0,0], [ymin, ymax], 'k', [xmin, xmax], [0, 0], 'k')
grid on
axis([xmin xmax ymin ymax])

% Actual root:
precision = 20; % the precision to use in num2str calls in this script
disp(['sqrt(3) = ', num2str(sqrt(3), precision)])

sqrt(3) = 1.7320508075688772

Bisection method

x_L = 1;
x_R = 2;
if sign(f(x_L)) == sign(f(x_R))
    error('guesses must bracket zero')
end

fprintf('iter %10s  %10s  %10s  %10s  %10s  %10s\n', 'x_left',...
    'f(x_left)', 'x_right', 'f(x_right)', 'x_new', 'f(x_new)')

epsilon = 1e-12;  % threshold

done = 0;
iteration = 0;
while ~done
    iteration = iteration+1;
    fprintf('%2d:  %10.8f  %10.8f  %10.8f  %10.8f', ...
            iteration, x_L, f(x_L),x_R, f(x_R))

    x_new = (x_L + x_R)/2;
    if abs(f(x_new)) < epsilon
        done = 1;
    elseif sign(f(x_new)) == sign(f(x_L))
        x_L = x_new;
    else
        x_R = x_new;
    end

    fprintf('  %10.8f  %10.8f\n',  x_new, f(x_new))
end

disp(['root = ', num2str(x_new, precision)])
perc_error=abs(sqrt(3)-x_new)/sqrt(3)*100;
disp(['% error = ' num2str(perc_error, precision) ' %'])

iter     x_left   f(x_left)     x_right  f(x_right)       x_new    f(x_new)
 1:  1.00000000  4.00000000  2.00000000  -2.00000000  1.50000000  1.50000000
 2:  1.50000000  1.50000000  2.00000000  -2.00000000  1.75000000  -0.12500000
 3:  1.50000000  1.50000000  1.75000000  -0.12500000  1.62500000  0.71875000
 4:  1.62500000  0.71875000  1.75000000  -0.12500000  1.68750000  0.30468750
 5:  1.68750000  0.30468750  1.75000000  -0.12500000  1.71875000  0.09179688
 6:  1.71875000  0.09179688  1.75000000  -0.12500000  1.73437500  -0.01611328
 7:  1.71875000  0.09179688  1.73437500  -0.01611328  1.72656250  0.03796387
 8:  1.72656250  0.03796387  1.73437500  -0.01611328  1.73046875  0.01095581
 9:  1.73046875  0.01095581  1.73437500  -0.01611328  1.73242188  -0.00257111
10:  1.73046875  0.01095581  1.73242188  -0.00257111  1.73144531  0.00419426
11:  1.73144531  0.00419426  1.73242188  -0.00257111  1.73193359  0.00081205
12:  1.73193359  0.00081205  1.73242188  -0.00257111  1.73217773  -0.00087941
13:  1.73193359  0.00081205  1.73217773  -0.00087941  1.73205566  -0.00003365
14:  1.73193359  0.00081205  1.73205566  -0.00003365  1.73199463  0.00038921
15:  1.73199463  0.00038921  1.73205566  -0.00003365  1.73202515  0.00017778
16:  1.73202515  0.00017778  1.73205566  -0.00003365  1.73204041  0.00007207
17:  1.73204041  0.00007207  1.73205566  -0.00003365  1.73204803  0.00001921
18:  1.73204803  0.00001921  1.73205566  -0.00003365  1.73205185  -0.00000722
19:  1.73204803  0.00001921  1.73205185  -0.00000722  1.73204994  0.00000600
20:  1.73204994  0.00000600  1.73205185  -0.00000722  1.73205090  -0.00000061
21:  1.73204994  0.00000600  1.73205090  -0.00000061  1.73205042  0.00000269
22:  1.73205042  0.00000269  1.73205090  -0.00000061  1.73205066  0.00000104
23:  1.73205066  0.00000104  1.73205090  -0.00000061  1.73205078  0.00000022
24:  1.73205078  0.00000022  1.73205090  -0.00000061  1.73205084  -0.00000020
25:  1.73205078  0.00000022  1.73205084  -0.00000020  1.73205081  0.00000001
26:  1.73205081  0.00000001  1.73205084  -0.00000020  1.73205082  -0.00000009
27:  1.73205081  0.00000001  1.73205082  -0.00000009  1.73205081  -0.00000004
28:  1.73205081  0.00000001  1.73205081  -0.00000004  1.73205081  -0.00000002
29:  1.73205081  0.00000001  1.73205081  -0.00000002  1.73205081  -0.00000000
30:  1.73205081  0.00000001  1.73205081  -0.00000000  1.73205081  0.00000000
31:  1.73205081  0.00000000  1.73205081  -0.00000000  1.73205081  -0.00000000
32:  1.73205081  0.00000000  1.73205081  -0.00000000  1.73205081  0.00000000
33:  1.73205081  0.00000000  1.73205081  -0.00000000  1.73205081  0.00000000
34:  1.73205081  0.00000000  1.73205081  -0.00000000  1.73205081  -0.00000000
35:  1.73205081  0.00000000  1.73205081  -0.00000000  1.73205081  -0.00000000
36:  1.73205081  0.00000000  1.73205081  -0.00000000  1.73205081  -0.00000000
37:  1.73205081  0.00000000  1.73205081  -0.00000000  1.73205081  -0.00000000
38:  1.73205081  0.00000000  1.73205081  -0.00000000  1.73205081  0.00000000
39:  1.73205081  0.00000000  1.73205081  -0.00000000  1.73205081  -0.00000000
40:  1.73205081  0.00000000  1.73205081  -0.00000000  1.73205081  -0.00000000
41:  1.73205081  0.00000000  1.73205081  -0.00000000  1.73205081  0.00000000
42:  1.73205081  0.00000000  1.73205081  -0.00000000  1.73205081  0.00000000
root = 1.7320508075688394
% error = 2.1793577112347061e-12 %

Newton's method

Newton's method requires also the derivative of the function. The derivative of this function is:

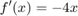
% Define a function handle for the derivative
fprime = @(x)-4*x;

x(1) = 2; % initial guess

n = 1;
while abs(f(x(n))) > epsilon && n < 50
    n = n+1;
    x(n) =  x(n-1) - f(x(n-1))/fprime(x(n-1));
end

% display successive approximations from Newton's method
for k = 1 : length(x)
    disp(['x(', num2str(k), ') = ', num2str(x(k), precision)])
end

x_root = x(length(x));
disp(['root = ', num2str(x_root, precision)])
perc_error=abs(sqrt(3)-x_root)/sqrt(3)*100;
disp(['% error = ' num2str(perc_error, precision) ' %'])

x(1) = 2
x(2) = 1.75
x(3) = 1.7321428571428572
x(4) = 1.7320508100147276
x(5) = 1.7320508075688772
root = 1.7320508075688772
% error = 0 %

Published with MATLAB® R2016b