Binary search trees work great if they are relatively balanced, but if care is not taken, they can become long and spindly. If data is inserted in random order, the tree will be "bushy" (and hence not too deep) with very high probability. Unfortunately, if the data is inserted in sorted (or nearly sorted) order, a binary search tree degenerates to a simple sorted list, and lookup or insertion becomes O(n) rather than O(lg(n)).

In many applications, this "unlucky" case may be quite common.
One way to deal with this problem is to keep the tree completely balanced: Any time a node is added or deleted, the tree is reorganized if necessary to keep it balanced. Unfortunately, the rebalancing act may end up completely rebuilding the tree, thus wasting more time than it saves. The trick is to keep the tree "almost" balanced --- balanced enough to keep it bushy, but not so perfectly balanced that a small change requires a complete reorganization.
An AVL tree (named after its inventors, G. M. Adel'son-Vel'skii and and E. M. Landis) is a binary search tree in which no node has subtrees that differ in height by more than one level. In other words, every node is balanced (its left and right subtrees are the same height), left-tall (its left subtree is one level higher than its right subtree), or right-tall (its right subtree is one level higher than its left subtree). First we show that an AVL tree is .q "balanced enough" to guarantee that it won't be too deep (so lookups, insertions and deletions will be fast). Then we show how an insertion or deletion that violates the AVL balance requirement can be quickly repaired.
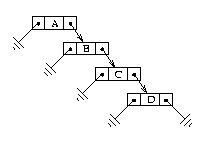
In the worst-case (least bushy) AVL tree, the only balanced nodes are leaves; all the other nodes are left-tall or right-tall. For example, here is a worst-case tree of height 5, in which all internal nodes are left-tall:
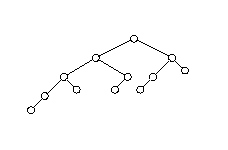
Note that the left subtree is a worst-case tree of height 4 and the right subtree is a worst-case tree of height 3. In general, a worst-case AVL tree of height h consists of a root and two subtrees, one a worst case AVL tree of height h-1 and the other a worst-case AVL tree of height h-2. It can be proved that in the height of a worst case AVL tree is approximately 1.44*lg(n), where n is the number of nodes in the tree. Since this is the worst possible case, searching an AVL tree with n nodes is guaranteed to require no more than O(lg(n)) operations.
The best (bushiest) tree of height h is the complete binary tree, which has 2h-1 nodes, so h is approximately lg(n) in the best case. Thus the worst AVL tree is only about 1.44 times as bad as the best possible one.
To put this in perspective, suppose we insert one million records into a binary search tree. If we are really lucky and the tree comes out completely balanced, its height will be 20, meaning that no lookup (or insertion or deletion) will require more than 20 operations. However, if we are unlucky and the records arrive in nearly sorted order, we will end up with a spindly tree like the one shown above and a random lookup will require 500,000 comparisons on the average. On the other hand, the worst-case AVL tree of height 29 has 1,346,268 nodes, so an AVL tree with one million records is guaranteed to have height no greater than 29, and lookups will never need more than 29 comparisons.
Suppose the root of the tree is left-tall and we insert a new value that is less than the value stored in the root. The BST member function insert will add a new node to the left subtree, which might make it taller. If so, the AVL balance condition will be violated: Before the insertion, the left tree was taller than the right tree. When the left tree gets still taller, it becomes two levels higher than the right tree. We will fix this by inserting some new "rebalancing" code just after calling the original BST insert. The rebalancing code checks whether the heights of the two subtrees differ by two levels, and if so, adjusts a few links in the vicinity of the root to make the tree "balanced enough" again.
After the performing the normal BST insert, but before rebalancing the root, the tree looks like this:
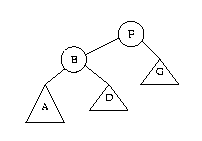
where the tree labeled A contains values less than B, the tree labeled D contains values between B and F, and the tree labeled G contains values greater than F. Let h be the height of the tree G. We are assuming that the root got out of balance because a node was added to its left subtree. Thus the left subtree must have height h+2. The main trick is to restore the AVL balance condition by rotating the tree to the right. A single right rotation makes B the root rather than F, thus raising B and lowering F:
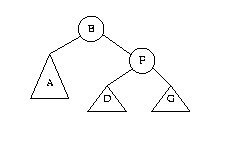
Note that the left-to-right ordering condition required of binary search trees still holds.
Does the rotation always restore the balance condition? Unfortunately not. There are three cases to consider: The subtree rooted at node B is left-tall, right-tall, or balanced. First suppose B is left-tall before the rotation. Then tree A has height h+1, tree D has height h, and the rotation has this effect:
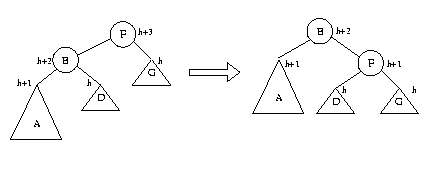
After the rotation, F and B are both balanced, and the whole tree is AVL. The case in which B is balanced before the rotation is similar, although in this case, F becomes left-tall and B becomes right-tall (try it yourself!). But the case in which B is right-tall before the rotation has a problem:
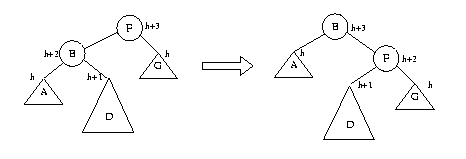
In this case, the rotation over-does it. Instead of a left tree that is two levels higher than the right tree, we end up with a right tree that is two levels higher than the left tree.
In this case (and only in this case), we have to do something a little more complicated. Since tree D has height h+1, we know it is not empty. In other words, before the rotation, the tree looks like this:
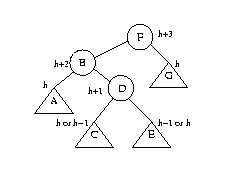
where each of C and E has height h or h - 1. In this case, we can do a double rotation to get a tree that satisfies the AVL balance condition:
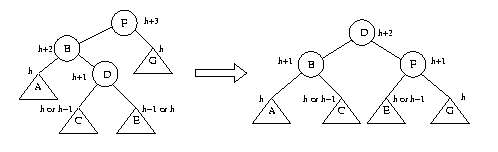
The same technique can be used for deletions. After performing a basic binary search tree remove to remove a node from one of the children, AVL's remove must check to see if one of the resulting subtrees is two levels higher than the other (it cannot be worse than that), and if so, do a single or double rotation to restore the AVL condition.
By the way, it is interesting to note that in all but one of the cases where we needed to do a rotation (single or double), the final tree ends up having the same height as the original tree before the insertion: h+2. The only exception is the case where B is balanced, and it can be shown that this case cannot arise for a single insertion. Thus each insertion will cause at most one rotation anywhere in the tree. (But deletion may cause more than one rotation.)