Here's the top-level schematic of the register file. I've implemented it with clock gating and using muxes to select the output, though other variations are possible.

Here's the simulation results:

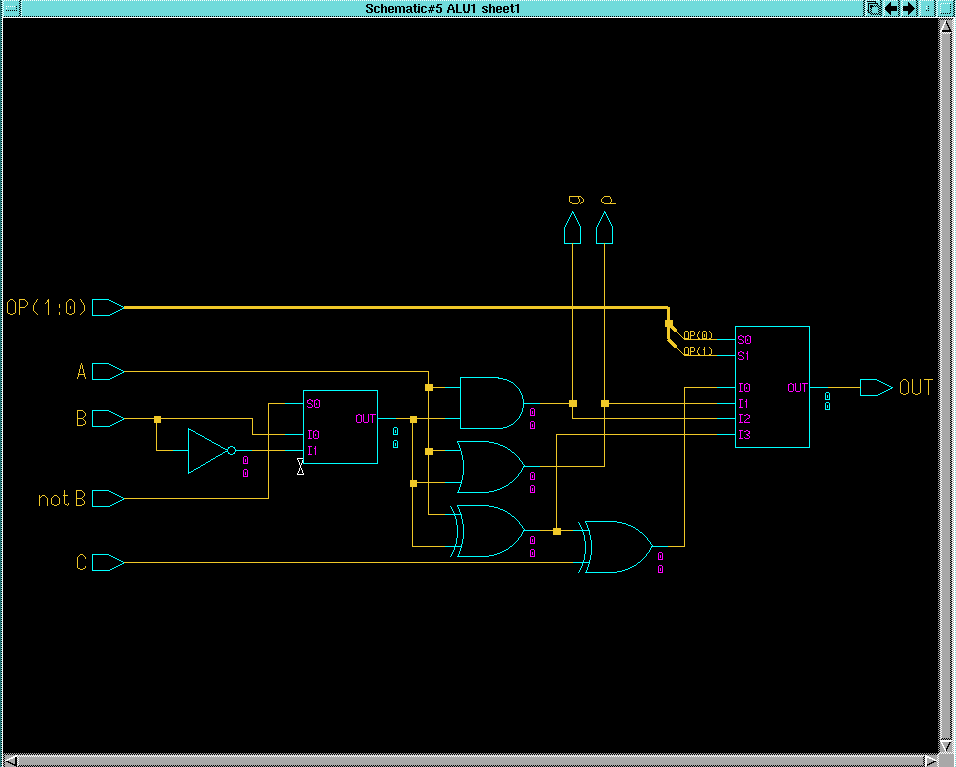
Schematic for the 1-bit ALU:
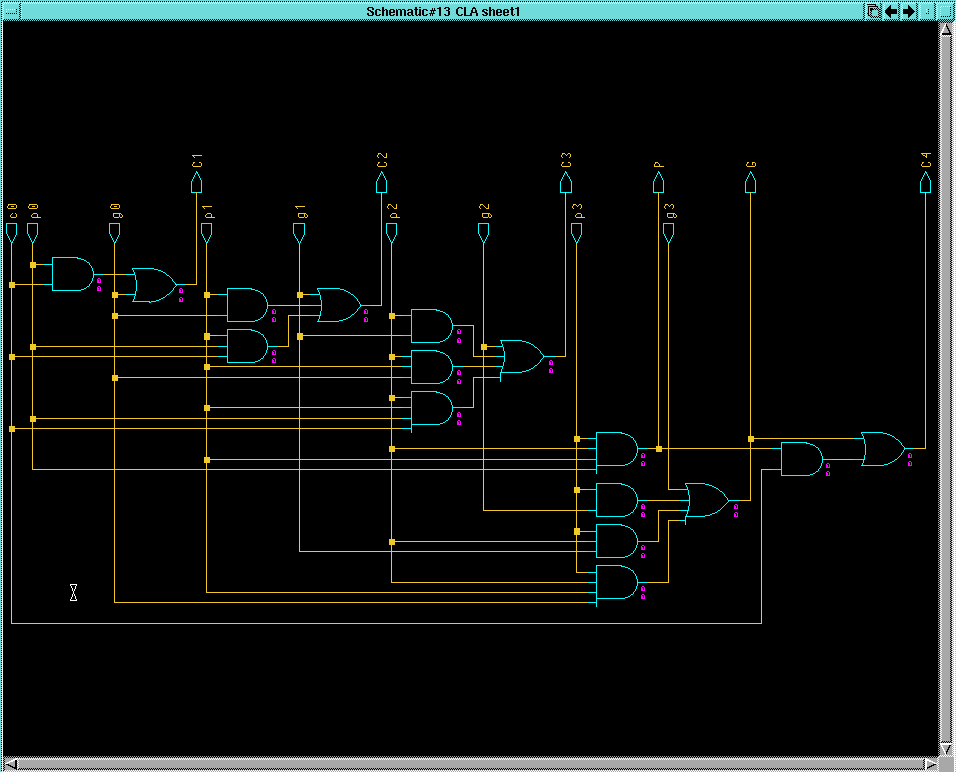
Schematic for the carry-lookahead unit:
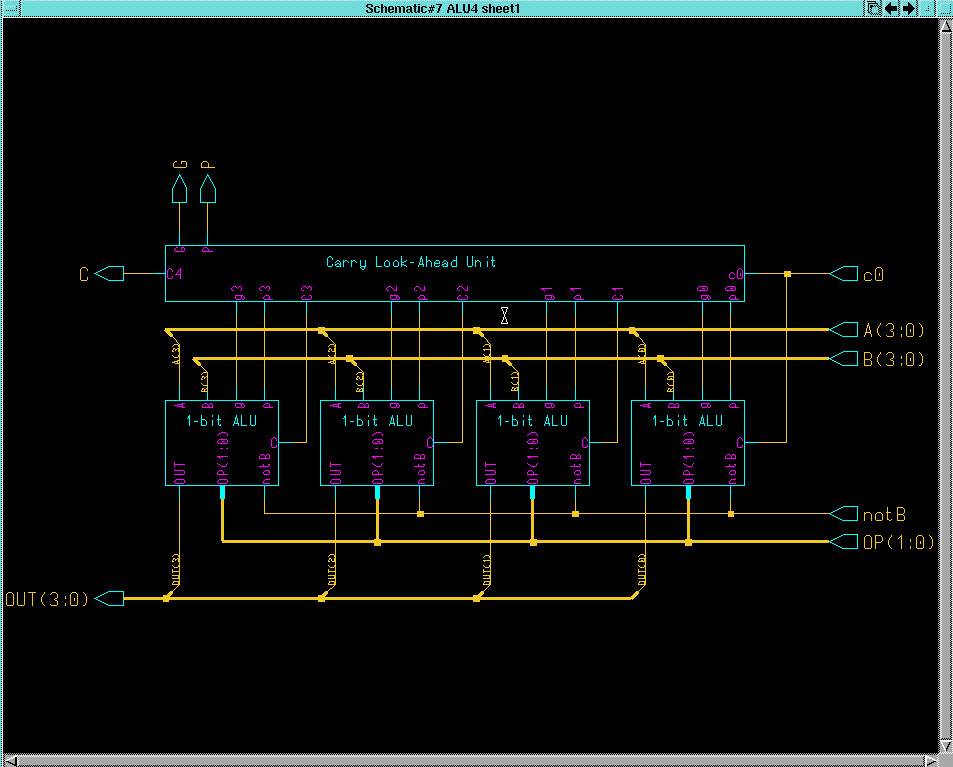
Schematic for the 4-bit ALU:
Schematic for the 16-bit ALU:

Schematic for the zero detect:

Schematic for the overflow detect:

An even simpler way to detect overflow is to compare C15 with C16...if they are different, an overflow occured.
Simulation of the ALU:

Problem 2.13 on page 92
Using compiler C1:
M1 - 400 MHz / (0.3 * 4 CPI + 0.5 * 6 CPI + 0.2 * 8 CPI) = 69 MIPS
M2 - 200 MHz / (0.3 * 2 CPI + 0.5 * 4 CPI + 0.2 * 3 CPI) = 63 MIPS
Using compiler C2:
M1 - 400 MHz / (0.3 * 4 CPI + 0.2 * 6 CPI + 0.5 * 8 CPI) = 63 MIPS
M2 - 200 MHz / (0.3 * 2 CPI + 0.2 * 4 CPI + 0.5 * 3 CPI) = 69 MIPS
Using 3rd-party compiler:
M1 - 400 MHz / (0.5 * 4 CPI + 0.3 * 6 CPI + 0.2 * 8 CPI) = 74 MIPS
M2 - 200 MHz / (0.5 * 2 CPI + 0.3 * 4 CPI + 0.2 * 3 CPI) = 71 MIPS
Using C1, M1 is the fastest. Using C2, M2 is the fastest. The 3rd-party compiler produces the fastest code on M1 and M2. Since M1 is the fastest in two of the three cases, it would be the best choice.
Problem 2.18, 2.20 on pages 93-94
Mbase: CPI = 0.4 * 2 + 0.25 * 3 + 0.25 * 3 + 0.1 * 5 = 2.8 CPI
Mopt: CPI = 0.4 * 2 + 0.25 * 2 + 0.25 * 3 + 0.1 * 4 = 2.45 CPI
Mbase: 500 MHz / 2.8 CPI = 179 MIPS
Mopt: 600 MHz / 2.45 CPI = 245 MIPS
Mopt is 245 / 179 = 1.37 times faster than Mbase.
Problem 2.31
Assume 100 instructions: 10 multiply, 90 other
Time spend on multiplication = (10 instr * 12 CPI) / (10 instr * 12 CPI + 90 instr * 4 CPI ) = 25 %
Problem 2.32
Avg CPI of Machine without modifictation (CPIold) = 0.1*12 + 0.9*4 = 4.8
Avg. time to excecute one instruction (Timeold) = 4.8 CPI/ x MHz
Avg CPI of Machine with modification (CPInew) = 0.1*6 + 0.9*4 = 4.2
Avg. time to excecute one instruction (Timenew) = 4.2 CPI/ (x/1.2 MHz ) = 5.04 CPI / x MHz
Since Timeold/ Timenew = 0.95 , the machine without modification is faster so the modification should not be done.
Amdahl's Law: Speedup = Execution Time (old) / Execution Time (new) = 1 / ((1 - Fractionenhanced) + Fractionenhanced / Speedupenhanced)
Speedup = 1 / ( 1 - 0.5 + 0.5 / 5) = 1.67
Multiply optimization: Speedup = 1 / (1 - 0.2 + 0.2 / 4) = 1.18
Memory optimization: Speedup = 1 / (1 - 0.5 + 0.5 / 2) = 1.33
Both: Speedup = 1 / (1 - 0.2 - 0.5 + 0.2 / 4 + 0.5 / 2) = 1.67