One-to-all broadcast algorithms

Section#11: One-to-all broadcast algorithms
(CS838: Topics in parallel computing, CS1221, Tue, Mar 2, 1999, 8:00-9:15 a.m.)

The contents

Communication models
Performance metrics
An example of lower bound calculations
Store-and-forward one-to-all broadcast
Wormhole switching one-to-all broadcast

In one-to-all broadcast, one designated node, called source, has a packet which must be sent to all the other processors. It is the simplest and most fundamental collective communication operation. Nowadays, it is a standard component of parallel SW libraries and is supported in HW in many commercial parallel computers. OAB is used in many parallel algorithms, such as vector-matrix multiplication, Gaussian elimination and LU factorization, Householder transformations.

Back to the beginning of the page

Back to the CS838 class schedule

Communication models

The design of optimal collective communication algorithms must take a number of constraints of the underlying network into consideration. In this text, we will model these constraints using the following parameters:

the number of ports: we can have 1-port, k-port, or all port routers, depending on how many packets they are able to inject, eject, or forward in one step.
directedness of channels: channels can be simplex, half-duplex, or full-duplex
switching technique: we will consider mostly either store-and-forward (SF) or wormhole (WH) switching here.
packet manipulation capability: this is a very important assumption
- combining model: we assume that every router is able to assemble the information received in previous round or rounds and combine it into new packets/messages which are sent further as a unit of communication. The model usually assumes that the combining operation involves no overhead, which is not always realistic. Manufacturers tend to make routers simple and cheap and this capability is usually not implementable in HW, which does imply a considerable SW overhead, especially if this functionality is implemented in the local processing node. Combining of packets is relevant mostly to SF rather than WH switching.
- noncombining model: packets travel as separate units of communication, routers can just buffer, switch, and forward them. This is a realistic model, implemented in most machines today.
- intermediate reception capability: an intermediate router can split the flow of flits into two streams so that it can forward a packet to the next router while copying the flits into the local node memory on-the-fly with no extra time penalty. This functionality is compatible mainly with WH switching, it can be implemented as a simple extension of WH routing.

Back to the beginning of the page

Back to the CS838 class schedule

Performance metrics

The efficiency of communication algorithms can be evaluated using several criteria. Their choice depends on the communication model and hardware.

time complexity:
- constant time model: we can just count the number of rounds or steps, assuming that all rounds take the same time, independently of the size of packets, for example.
  - in SF networks, we can count also the number of transmissions (= hops),
  - in WH networks, we count usually the number of startup rounds.
- linear time model: we can calculate for example the base network latency, considering the message size and bandwidth, routing, and switching times. We have derived formulae for base network latency in Section #7.
  - in SF networks, except for calculating the total network latency, we can calculate the total communication work, where each packet of size M travelling on distance d contributes with dM
  - in WH networks, we can calculate the exact total network latency.
intra-router auxiliary buffer requirements: as in the permutation routing problems in the last two sections, there is often a trade-off between the time complexity and the size of intra-router buffers. We will denote the maximum requirements on router buffers by \beta. This parameter is relevant mostly to SF networks, WH router have usually \beta=0.
communication efficiency: to achieve time optimality, collective communication algorithms should
- use the full bandwidth of the network, i.e., be able to utilize all the available channels and buffers during the whole operation,
- eliminate redundancies in the information dissemination, i.e., avoid sending the same information to nodes more than once (so called NODUP = NO-DUPlication condition) or avoid nodes from receiving the same packet back (NOHO = NO-node-Hears-its-Own-information condition)

Back to the beginning of the page

Back to the CS838 class schedule

An example of lower bound calculations

Lemma

The lower bounds on the time and transmission complexity of four basic collective communication operations in all-port full-duplex SF noncombining Q_n in constant-time model are given in the following table.

comm. operation # of rounds # of transmissions

OAB n 2ⁿ-1

AAB [(2ⁿ-1)/n] 2ⁿ(2ⁿ-1)

OAS [(2ⁿ-1)/n] n2^n-1

AAS 2^n-1 n2^2n-1

Proof

SF OAB cannot take less rounds than is the value of the diameter. Since the broadcast packet has to be delivered to 2ⁿ-1 distinct nodes, the number of transmissions is at least 2ⁿ-1.
During AAB, each node has to receive 2ⁿ-1 distinct packets. In the all-port model, it can receive at most n packets in one round. Thus, at least [(2ⁿ-1)/n] rounds are needed. The number of transmissions is at least 2ⁿ times the number of transmissions of one OAB.
During OAS, the source has to inject the total of 2ⁿ-1 distinct packets and it can inject at most n packets in one round. There is n\choose k vertices of Q_n in the distance k from the source. The number of transmissions cannot be less than \sum_k=1ⁿk{n\choose k}=n2^n-1.
AAS consists of 2ⁿ OASs running concurrently. So, the number of transmissions is 2ⁿ times the number of transmissions in one OAS, i.e., n2^2n-1. Full-duplex all-port Q_n can perform n2ⁿ hops in one round. Thus, the minimum number of rounds is ((n/2)2²ⁿ)/(n2ⁿ)=2^n-1.

It is noteworthy that there exist optimal hypercube algorithms matching exactly these lower bounds and we will describe some of them in the following four sections.

Back to the beginning of the page

Back to the CS838 class schedule

Store-and-forward one-to-all broadcast

Clearly, half-duplex channels are sufficient for OAB, full-duplex channels cannot improve anything.

1-port vs.~all-port model

Any all-port SF network has a trivial optimal OAB with the number of rounds equal to its diameter, called flooding algorithm. It works for hypercubic networks, mesh-based networks, and shuffle-based networks. The source sends the packet to all its neighbors, which make a copy of it and forward it to all its remaining neighbors. Even though the packet is never sent back, some nodes can receive the packet more than once if the graph contains cycles. To avoid the duplication, broadcast algorithms are designed to send the packet only along edges of spanning trees of minimum height, called shortest-path spanning trees or broadcast trees.

On the other hand, optimal OAB algorithms are harder to find for 1-port SF networks. The

trivial lower bound on the number of rounds of OAB in 1-port SF network G is max(diam(G),log |V(G)|), since in one round, the number of informed nodes can double at most. It can be generalized to the case of a k-port G, the trivial lower bound on the number of rounds of OAB in k-port SF network G is max(diam(G),log_k+1 |V(G)|). However, the problem to determine the optimal time complexity of OAB (= nontrivial lower bound) in 1-port SF network G is NP-complete. Fortunately, for most SF networks, optimal OAB algorithms are known.

EREW PRAM

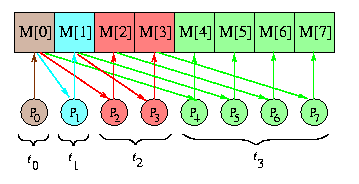
CAPTION: EREW PRAM one-to-all broadcast with 8 processors.
Obviously, EREW PRAM is constrained in the same way as an 1-port network. In the first step, the source writes the data into a shared memory cell. The standard optimal algorithm then just doubles the number of copies of the data in the shared memory in every step, as implied by Figure . As a result, the number of informed processors doubles, too. Therefore, the number of steps matches the trivial lower bound [log p].

It is noteworthy that exactly the same doubling algorithm works for 1-port complete network.

Hypercube

Interestingly enough, the hypercube allows exactly the same optimal broadcast algorithm, since its symmetric and binary recursive topology fits perfectly to this communication scheme.

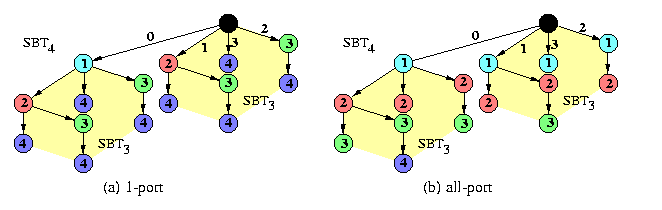
CAPTION: Spanning binomial trees in 1-port and all-port Q₄.
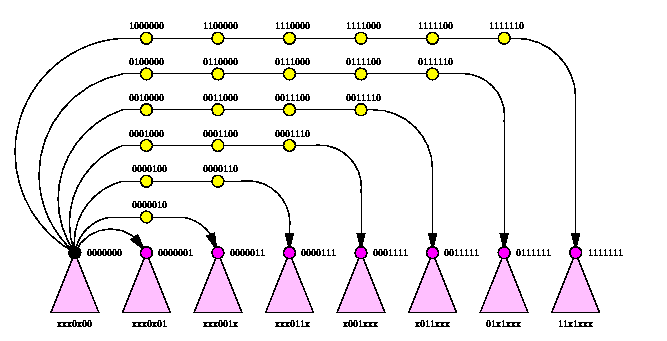
The corresponding spanning tree of Q_n is called n-level spanning binomial tree, SBT_n. In fact, it is isomorphic to the D&C tree of Q_n explained in Section #7. Figure illustrates the recursive structure of SBT_n: SBT₀ is a single node and SBT_n is constructed from two SBT_n-1's by linking their roots with a new edge and by making either of them the new root. Since the hypercube is both vertex and edge symmetric, we can place the root of a SBT in any hypercube node and use the hypercube dimensions in any order.

The SBT algorithm works optimally for both 1-port and {\em all-port hypercube.} In Figure , the edge labels are the dimension numbers. Each vertex has a label corresponding to the round number in which it receives the packet. The number of nodes that receive the packet in round i is 2^i-1 in the 1-port model, whereas n\choose i in the all-port model (therefore the name binomial tree). Clearly \sum_i=1ⁿ2^i-1=\sum_i=1ⁿ{n\choose i}=2ⁿ-1. Both schemes are transmission optimal.

Meshes

An optimal OAB in a SF 1-D mesh is basically the flooding algorithm: Send the packet to both directions in pipeline. In 1-port case, send it in one direction, then in the other, starting with the longer-path-ahead one (again the farthest-first strategy) In n-dimensional meshes, dimension-order approach is necessary to avoid duplication. Every node uses dimensions in the same order, say 1,...,n, so that the communication pattern generates dimension-order spanning trees, which are basically generalizations of hypercube binomial trees. The downward (upward) direction of dimension i will be denoted i- (i+, respectively).

All-port meshes

The source can be any internal node. It will start OAB just by sending the packet to all output channels. Every other node will execute the following node algorithm:

if the packet arrived via channel of direction i, where 0<= i<= n-1,

then forward it in direction i further (if possible) and simultaneously send it

to all neighbors in directions j=i+1,..., n-1 upward and downward (if they exist)

The number of rounds is equal to the diameter at most, since it is again a flooding algorithm, just ``dimension-controlled''.

1-port meshes

The source can be again any internal node. It starts by sending the packet along the first dimension, first to the direction with the longer path ahead, and then it injects the packet sequentially into channels of further directions 2-,2+,...,n-,n+.
Every other node will execute the following node algorithm:

if the packet arrived via channel in dimension i, where 0<= i<= n-1,

then

{ if you are not the last node in direction i, then forward it in direction i further;

for j=i+1,..., n-1 do_sequentially

{ if you are not the first node in dimension j, then forward it in direction j-;

if you are not the last node in dimension j, then forward it in direction j+;

}

Figure depicts such a tree. The numbers within nodes are again the rounds in which the node receives the packet.

CAPTION: Dimension-order OAB tree in 1-port store-and-forward M(3,3,4).
The farthest-first approach provides tight time optimality, except for the case when the first dimension has odd size and the source is exactly in the middle of it. We can conclude that

dimension-order spanning trees give optimal OABs for both 1-port and {\em all-port meshes.} A general formula for calculating the broadcast time on a SF mesh M(...) is

t_OAB(M(...))<=(t_s+t_d+mt_m)diam(M(...)).

Tori

Tori are vertex symmetric, so that we can use the mesh algorithm above with the source sitting in the middle of the mesh. Without any precautions, we will have duplication of packets in final rounds in each cycle. There are two solutions:

to ignore the second packet, so that in each cycle of the torus, one hop will be superfluous,
to prevent one of two nodes opposite to the source within each cycle to forward the packet. This would require some additional information in the packet header.

Back to the beginning of the page

Back to the CS838 class schedule

Wormhole switching one-to-all broadcast

1-port vs.~all-port model

The time lower bound in one-port WH network is log |V(G)|. The diameter lower bound does not apply, since the communication is distance-insensitive. 1-port meshes and tori can easily achieve this lower bound by simulating the hypercube broadcast scheme. On the other hand, the lower bound for all-port meshes and tori is much harder to achieve, we will describe some known results.

Hypercube

In 1-port Q_n, WH routing does not provide any improvement compared to SF, since the SBT_n-based SF algorithm with time complexity (t_s+t_d+mt_m)n is optimal. Under the all-port assumption, however the WH routing can provide improvement for larger n, since the lower bound on the number of rounds becomes [ n/log(n+1)] (the number of informed nodes can increase n times in every round). The first improvement is so called double tree algorithm (DTA). It is a simple variation of the SBT algorithm which requires [ n/2] rounds for all-port WH Q_n. The idea is to send the packet to the node s', complement to the source s, in the first round, in parallel with sending the packet to all neighbors of s not involved in the communication with s'. Then both s and s' build partial SBTs as implied by Figure .

CAPTION: 2-round OAB in all-port WH Q₄
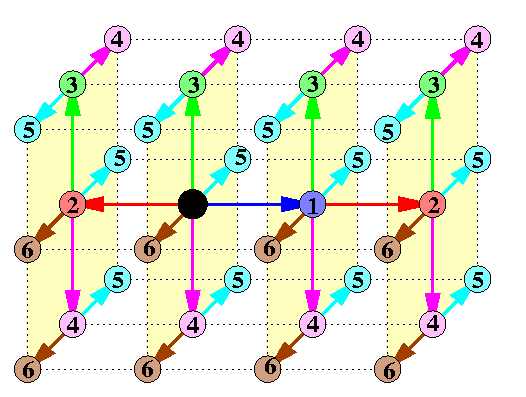
DTA is really approximately twice faster on real machines than the standard SBT algorithm, but it is optimal only for n<= 6. An algorithm which is optimal up to a small multiplicative constant for n>= 7 is called Ho-Kao algorithm (HKA) and it is based on the following idea: divide recursively Q_n into sufficiently small subcubes of nearly equal size and apply DTA inside these subcubes. HKA assumes e-cube routing with checking the bits left-to-right and uses ascending dimension-simple paths: Given a sequence of dimension numbers 0<= i₁ < ... < i_d<= n-1, d<= n-1, an ascending dimension-simple path is any path u₀,...,u_d of nodes in Q_n such that u_j is obtained from u_j-1 by complementing bit i_j. It follows that all d paths u₀-> u_j are pairwise node-disjoint if e-cube WH routing is used, so that u₀ can send d packets to all these destinations simultaneously. HKA constructs an ascending dimension-simple path u₀,...,u_n such that Q_n can be partitioned into n+1 disjoint subcubes S_i, of equal or nearly equal size, such that subcube S_i contains u_i. Figure demonstrates the idea for n=7.

CAPTION: Time optimal OAB algorithm in all-port WH Q₇.

One-port WH Meshes

For one-port WH meshes, there exists a simple optimal OAB algorithm. The copies of the packet are disseminated dimension by dimension (cartesian product property), but this time, every node must participate in broadcasting in one dimension the whole time, until all nodes in respective linear paths are informed, since the basic procedure is the recursive doubling instead of trivial SF pipelining. The linear paths are recursively split into halves and in each new half, a new source is chosen. Since WH switching is distance insensitive, this provides always the logarithmic number of rounds. 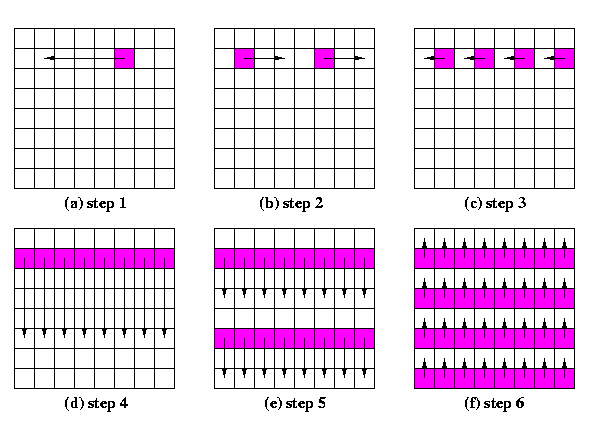A closer look reveals that it is basically a simulation of the SF hypercube SBT-based algorithm. Consider M(z₁,...,z_n) with source (a₁,...,a_n). The broadcast tree develops in phases in the dimension order 1,...,n. In phase i, all informed nodes form submesh M(*ⁱ,a_i+1,...,a_n). In phase i+1, all informed nodes become sources in linear arrays along dimension i+1. Since meshes are not symmetric, the behavior of the algorithm depends on the position of the source. Figure gives the idea which can be easily generalized

CAPTION: A generic OAB scheme for one-port WH meshes

for any position of source by choosing correct directions of packet dissemination,
for mesh of any dimensionality by applying the cartesian product property. Note that the order in which the dimensions are chosen is irrelevant.
for any sizes z_i of mesh sides. If z_i is not a power of two, the algorithm's pattern for that dimension uses exactly the same binary splitting, except that some nodes can idle in a given round, since they cannot establish a new source in a new division. Due to that, a care must be taken to synchronize the communication requests and force that idling nodes to wait for the next round.

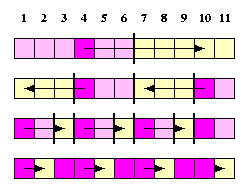
CAPTION: Recursive doubling if the size of the mesh is not a power of two.

One-port WH tori

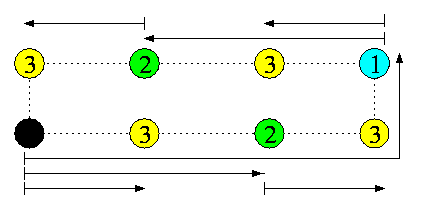
Optimal-time OAB algorithm uses again recursive doubling, dimension-by-dimension, but due to vertex-symmetry, it is much simpler. The reason is obvious from Figure showing 1D-torus. OAB in WH T(z) is exactly the same as OAB in WH M(z) with the source in the corner. The base network latency formula is also simple.

T_OAB(T(z))=\sum_i=1^{[log z]}(t_s+[\frac{z}{2ⁱ}] t_d+mt_m)=(t_s+mt_m)[log z] + t_d(z-1).

Compare this with the complexity for the SF model: T_OAB(T(z))=(t_s+t_d+mt_m)[\frac{z}{2}].

CAPTION: An optimal OAB in 1-port wormhole 1D-torus T(8) using recursive doubling.

All-port WH meshes and tori

The lower bound on the number of rounds of OAB in n-dimensional WH all-port mesh or torus with N nodes is log_2n+1N. To match this lower bound, every node, once involved in the broadcasting, must find in every round from the moment it was informed 2n uninformed nodes and deliver them the packet so that all these paths are arc-disjoint. This turned out to be a difficult problem and it has been addressed by the research community for about last 5 years as a challenging open problem. This effort seems to converge to solutions, the latest solutions provide nearly optimal results. We will mention here just some simpler discoveries made during this research quest.

Recursive tiling approach

One of the earliest attempts to solve the problem was inspired by the theory of recursive tiling of 2-D areas. Figure gives the intuition. Unfortunately, this approach

is applicable only to tori T(5^k,5^k),
does not use dimension-order routing for constructing the paths,

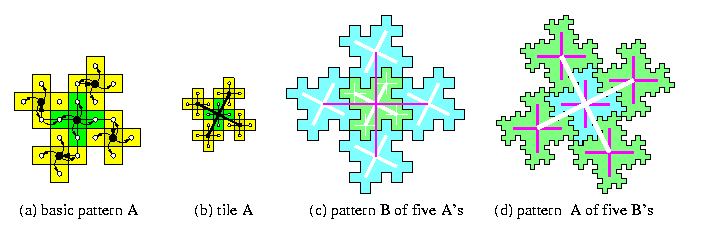
CAPTION: Tiling of torus T(5^k,5^k)

Extended dominating set approach

Definition

A set of dominating nodes D in a direct network G is a subset of nodes of G such that every node in G is

either in D
or is a neighbor of at least one node in D

The notion of dominating sets could be useful for SF networks, but it can generalized for WH networks to exploit the distance-insensitivity of routing.

Definition

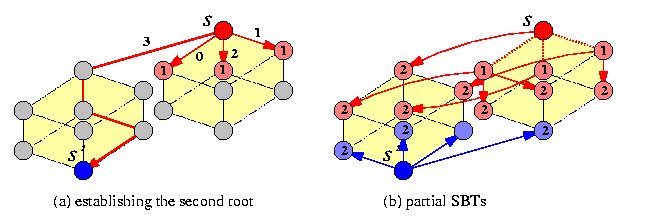
Consider an all-port WH direct network G with node set V, a routing algorithms R, and two subsets of nodes D₂\subset D₁\subseteq V. The set D₂ is said to be an extended dominating set (EDS) of D₁ if and only if there exists a set of link-disjoint paths under R such that every node in D₁-D₂ is reachable along one such path from some node in D₂.

Figure illustrates both concepts.

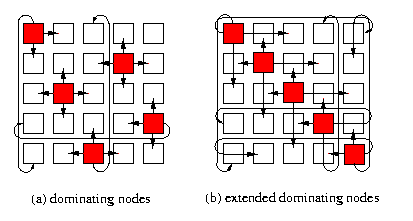
CAPTION: 5-node dominating set and extended dominating set in T(5,5)
The method works well for meshes M(4^k,4^k) and the basic idea is to build recursively a hierarchy of extended dominating nodes, where level-i EDNs are informed from all EDNs of levels j < i. Figure illustrates the construction of EDNs in mesh M(16,16) with XY routing. In the first two rounds, the source informs 4 level-3 EDNs. In round 3, these 4 nodes inform 12 level-2 EDNs. In round 4, every level-1 EDN receives one packet from either level-2 or level-3 EDN. After round 4, every uninformed node is dominated by at least one informed node so that in one more round, all nodes are informed.

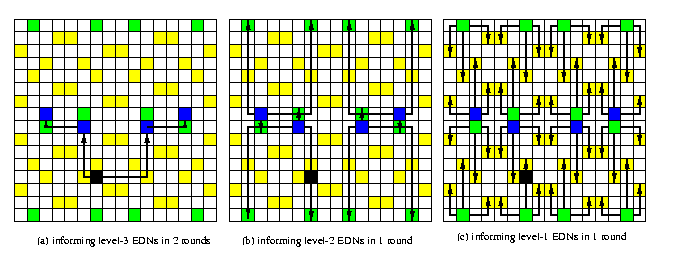
CAPTION: OAB in M(16,16) based on 3-level EDN hierarchy

Dilated-diagonal-based approach

This algorithm works optimally for 2-D tori T(5^k,5^k), but it can be generalized and applied to arbitrary 2-D torus, in which case it requires at most 5 rounds more than the lower bound. Assume for simplicity a square torus T(n,n). The algorithm exploits the vertex symmetry of tori. It consists of three phases:

Phase 1: Broadcast the packet into all rows so that each row contains exactly one copy. This can be done in [log₅n] rounds by recursive splitting the torus into 5 horizontal strips of approximatively the same width and sending the packet from the source's strip to all other 4 strips in one round along link-disjoint paths using XY routing.
Phase 2: Align the packets to the main diagonal in all rows in parallel. Hence, only one round is needed.
Phase 3: Each node on the main diagonal views the torus as decomposed into 5 diagonal bands of approximatively same width, the main diagonal is in the middle of the first one. In one step, it informs four nodes on middle diagonals of the other four bands so that all the 4n paths are pairwise link-disjoint. This is performed recursively in each diagonal band.

If the torus is not a square, the same idea is applied, except for using so called dilated diagonals.

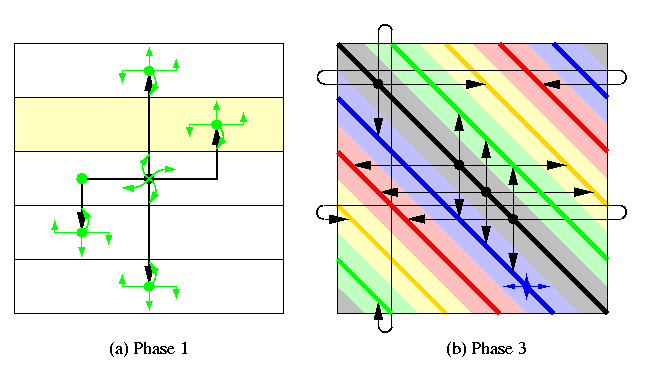
CAPTION: Dilated-diagonal-based OAB in a square torus.
Figure illustrates the recursive construction in phases 1 and 3.

Back to the beginning of the page Back to the CS838 class schedule


comm. operation	# of rounds	# of transmissions


OAB	n	2ⁿ-1

AAB	[(2ⁿ-1)/n]	2ⁿ(2ⁿ-1)

OAS	[(2ⁿ-1)/n]	n2^n-1

AAS	2^n-1	n2^2n-1

Section#11: One-to-all broadcast algorithms(CS838: Topics in parallel computing, CS1221, Tue, Mar 2, 1999, 8:00-9:15 a.m.)

The contents

Communication models

Performance metrics

An example of lower bound calculations

Store-and-forward one-to-all broadcast

1-port vs.~all-port model

EREW PRAM

Hypercube

Meshes

All-port meshes

1-port meshes

Tori

Wormhole switching one-to-all broadcast

1-port vs.~all-port model

Hypercube

One-port WH Meshes

One-port WH tori

All-port WH meshes and tori

Recursive tiling approach

Extended dominating set approach

Dilated-diagonal-based approach

Section#11: One-to-all broadcast algorithms
(CS838: Topics in parallel computing, CS1221, Tue, Mar 2, 1999, 8:00-9:15 a.m.)