Section#12: Multicast, IRC, and one-to-all scatter algorithms
(CS838: Topics in parallel computing, CS1221, Thu, Mar 4, 1999, 8:00-9:15 a.m.)
The contents
- Multicast
- Multicast in hypercubes
- Multicast in meshes
- Intermediate reception capability
- One-to-all broadcast with IRC
- One-to-all scatter
- Combining vs.~noncombining model
- 1-port vs.~all-port routers
- Noncombining model
- Combining model
Multicast
Multicast communication is a one-to-many communication pattern. It can be viewed as a broadcast to a subset of nodes of the network. In general, however, this subset does not necessary form a proper regular subnetwork. So application of a standard OAB algorithm can be very inefficient, especially in WH networks, since it could involve nodes other than the destination ones. On the other hand, a multicast may use, and in general must use, routers at other nodes to intermediate the packets. The problem here is that for given all-port WH network with a base routing function R, several simultaneous multicast requirements should use contention-free paths to achieve the best performance and avoid deadlocks.
Since this problem is hard in general, we will restrict the discussion to the mesh-based topologies. The key trick here is to enforce lexicographic ordering on the destinations induced by the given dimension-order routing.
Multicast in hypercubes
Paths between lexicographically ordered destinations using the e-cube routing in a hypercube have the following key property:
Lemma
Consider Qn with e-cube routing checking the address bits left-to-right. Let u < v < w < z be four lexicographically ordered nodes of Qn with respect to this dimension ordering (for example, 0100 < 0101 < 1000 < 1011 for n=4.) Then
- base routing paths u-> v and w-> z are link-disjoint,
- base routing paths v-> u and z-> w are link-disjoint,
- base routing paths v-> u and w-> z are link-disjoint,
- base routing paths u-> v and u-> z are not link-disjoint and the priority is given to u-> z,
- base routing paths u-> z and v-> w are not link-disjoint and the priority is given to u-> z.
Figure gives the intuition behind this result. This observation provides the algorithm for multicast.
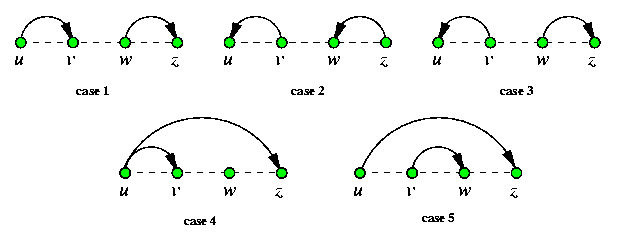
CAPTION: Disjointedness of base routing paths between lexicographically ordered hypercube nodes.
Due to vertex-symmetry, any multicast from a source s can be handled as a multicast from source 0n, just by applying translation u-> u XOR s. The sequence of lexicographically-ordered destinations is called dimension-order chain. Due to Lemma , we can apply again recursive doubling scheme on the chain, called chain multicast, which results in a logarithmic number of rounds!!! 1-port SBT-based OAB algorithm is just a special case of this scheme. Figure shows the idea on an example of a multicast from source 000 to nodes {0001, 0100, 0111, 1010,1011,1100} in Q4 in 3 rounds.
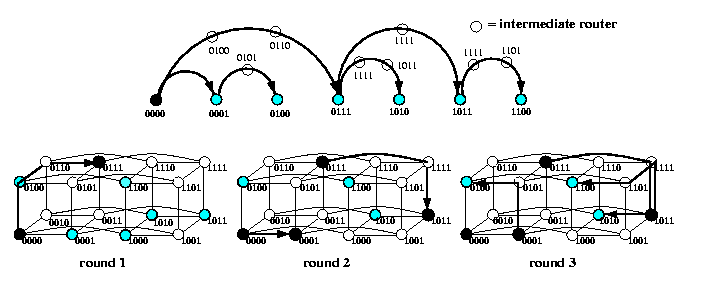
CAPTION: Multicast in Q4 to a dimension-ordered chain of destinations, assuming e-cube routing.
Multicast in meshes
The only difference compared to the hypercube is that meshes are not node-symmetric and the source can become an interior node in the dimension-order chain of destinations. Since Lemma applies similarly here, the recursive scheme is as follows:
- split the chain into two halves
- if the source is in the lower half, it sends the packet to the first node of the upper half
- otherwise, it sends the packet to the last node of the lower half
- apply recursively the same splitting to both halves
In all parts, except possibly for that with the source, chain algorithm is used, since the new source is always a boundary node of the chain.
CAPTION: Multicast in 2-D mesh with XY routing
Intermediate reception capability
Standard wormhole routers support only point-to-point routing of unicast packets: a packet has exactly one destination, intermediate routers only forward the data pipeline of flits, and only the router of the destination node absorbs the whole packet. This WH routing mechanism can be extended to support multidestination (= multicast) packets by so called intermediate reception capability (IRC). A single packet can have several destination addresses in header flits and every intermediate router whose address matches the first (= leading) destination address in the header performs a forward-and-absorb operation: it forwards the pipeline of flits to the next intermediate router while copying simultaneously the data flits into the local processor memory. Of course, the router must also remove the corresponding address flit from the header. If the leading destination address does not match the local router address, it just forwards the flits toward the destination. The last destination router absorbs the flit stream and removes it from the network by storing it into the local memory. Figure illustrates the idea on an example of a 4-destination packet.
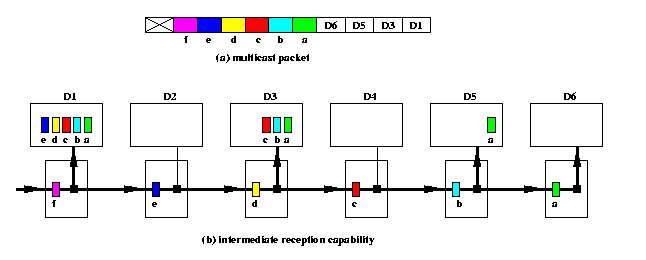
CAPTION: The structure of a multicast packet and a snapshot of its routing via routers with intermediate reception capability.
IRC is a very powerful mechanism that can be implemented easily in HW by a moderate extension of the standard WH router architecture with a marginal increase of the communication latency. It provides an excellent support for OAB and multicast operations. Obviously, the order, in which the destination addresses are listed in the header, determines the path through a network, since multicast packets are routed in a piecewise manner: A multicast packet from source s to destinations d1,...,dn is routed from s to d1, then from d1 to d2, and so on, using the base routing function, used for standard unicast packets, such as dimension-order routing in meshes.
Ideally, we would like to treat multicast packets as unicast packets, so for example, if the routing function is deadlock-free for unicast packets, it should be deadlock-free for multicast packets. Moreover, multicast and unicast packets should be able to co-exist safely in the network without modifications to the routing function. So, the obvious requirements on routing multicast packets are the following:
- At any intermediate destination, a multicast packet should be able to find a path to the next destination.
- The piecewise routing should not produce additional communication dependencies which could introduce cycles into the channel dependency graph and cause deadlocks.
Assuming the piecewise routing, it can be shown that these requirements are met if the order of destination addresses of multicast packets conforms to the basic routing function. Informally, this means that the concatenation of paths s-> d1, d1-> d2,...,dn-1-> dn is identical with a path s-> dn of a unicast packet from source s to destination dn constructed by the base routing function R.
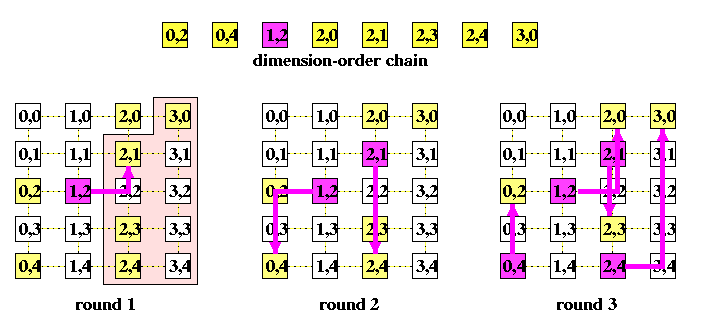
This strategy is called base routing conformed paths (BRCP) model. This provides also an efficient scheme for solving general multicast routing problems, Figure shows an example of a set of paths conformed to XY routing in a 2-D mesh performing a multicast operation in two rounds. The known upper bound on the number of rounds for an arbitrary multicast problem in M(z,z) using only R and C paths is [log(z+1)]+2, but the algorithm is rather complicated.
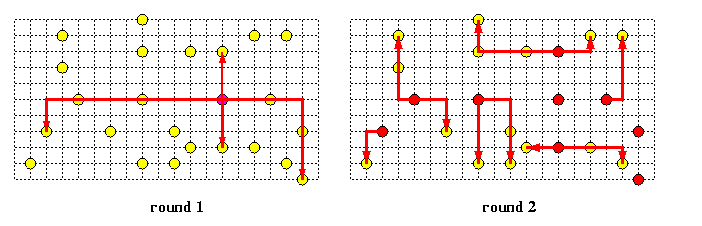
CAPTION: Implementation of a general multicast communication in two rounds using routing of multicast packets conformed to XY base routing in a 2-D mesh.
IRC provides a tremendous support for OAB operations. Consider WH M(a,b) with XY routing. Figure shows three different situations.
- The source is in the corner of a 2-D mesh: Figures (a) and (b) show two ways to implement OAB in two rounds. The former is called (C,R) and the latter (RC,C), where R=row and C=column. Of course, the (RC,R) scheme is possible, too.
- The source is an arbitrary node of M(a,b).
- A trivial scheme is to send a unicast packet to a corner node and apply the previous schemes. It takes 3 rounds.
- If a<= b+1, then there exist a 2-round scheme as shown on Figure (c). Assume source (x,y). In the first round, the source sends a multicast packet to one of the corners. For example, if b-y>= x-1, then we choose the upper right corner. From all informed nodes, all other nodes can be informed in one single round using disjoint R, C, and RC paths.
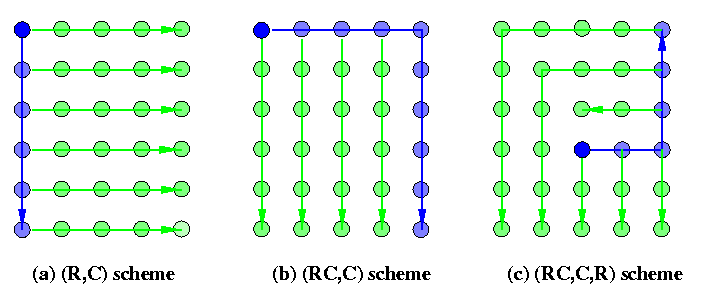
CAPTION: One-to-all broadcast schemes for 2-D meshes with IRC.
OAB in 2-D tori is even simpler. The generalization to n-dimensional meshes with dimension-order routing is straightforward, OAB can always be completed in n+1 rounds.
One-to-all scatter
In one-to-all scatter, also called one-to-all personalized communication or single-node scatter, one node sends different data to every other processor. At the start of an OAS, the source has N-1 packets of size M and at the end, each processor has one packet of size M. The algorithms for OAS depend very much on the underlying communication HW model. A naive OAS algorithm needs N-1 rounds.
In general, OAS has a similar complexity as AAB in many communication models: in AAB, each processor has to receive N-1 distinct packets, and in OAS, the source has to send N-1 distinct packets.
Combining vs.~noncombining model
In case of OAS, combining makes sense, in both SF and WH networks.
- combining model: OAS is then very much like OAB, except that the message size varies.
- SF switching: message pipelining is used. The source assembles all packets into one aggregate message for a given destination group of processors and each destination node just removes its own packet from the aggregate and forwards it further.
- WH switching: the same approach can be applied except that we can use some variant of recursive doubling instead of pipelining.
- noncombining model: the source sends all N-1 packets separately.
- SF switching: the farthest-first strategy applies since packets move in pipelines,
- WH switching: destinations can be chosen in any order.
1-port vs.~all-port routers
- all-port model: Let d be the degree of the source. To minimize the total time of the OAS operation, the source should build a spanning tree consisting of d subtrees of approximatively the same size.
- SF switching: the depth of all trees should be the same (so that the pipelines in all subtrees will take approximatively the same number of rounds).
- WH switching: the depth of subtrees can vary, but all the paths between the source and nodes in two different subtrees should be pairwise link-disjoint.
- one-port model: This case is trivial if we consider noncombining model. The source has to send N-1 packets and it can send only one in one round.
- SF switching: we can use for example a pipeline along a Hamiltonian path or any other routing using the farthest-first ordering of packets.
- WH switching: just any basic shortest-path routing can be used.
Noncombining model
Figure (a) shows the trivial scheme for a SF 1-D torus: sending the packets in pipeline using the farthest-first ordering. Figure (b) depicts an all-port scheme: two packets are sent in one round in both directions, using farthest-first ordering, the cycle is split into a left and right half, so that the number of rounds drops to one half. In case of WH routing, the ordering of packets is irrelevant. The variants for 1-D mesh are obvious.
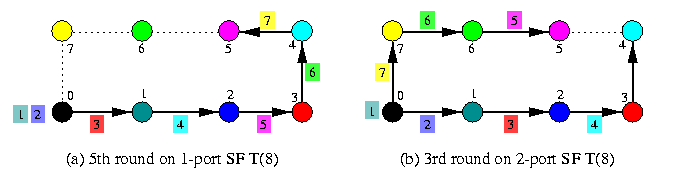
CAPTION: OAS in noncombining 1-D torus T(8).
The generalization to 1-port higher-dimensional meshes, tori, and hypercubes is trivial by cartesian-product property. Consider all-port networks. Regardless of whether we have SF or WH routing, an optimal OAS without combining packets requires a spanning tree with subtrees of approximately equal size reachable via link-disjoint paths from the source. It is a generalization of the scheme on Figure (b), which can always be done optimally for tori and hypercubes, but not always for meshes, the source is not always in the center of the mesh. In the following, a construction of such an optimal tree is explained for Qn.
All-port noncombining hypercube
Without loss of generality, let 0n be the source and the root of the scatter tree D and let Di, i=1,...,n, denote its subtrees. Our aim is to achieve [(2n-1)/n]<= |V(Di)|<= [(2n-1)/n]. The optimal number of hops can be attained if Di are shortest-path trees. The idea how to make all subtrees Di equally-sized and reachable along link-disjoint paths is the following:
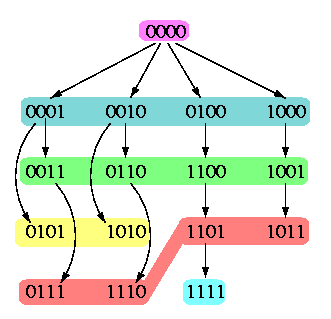
- All nonzero nodes are partitioned into equivalence classes Rk, 1<= k<= n-1, consisting of nodes with k 1's.
- The classes Rk are listed in ascending order by increasing number of 1's in the nodes: R1,...,Rn-1,Rn.
- Each Rk is split into necklaces Lkj, closed with respect to 1-bit rotation. Depending on the periodicity of nodes, each necklace consists of q nodes, where q=n (full necklaces) or q < n is a divisor of n (degenerate necklace),
- Necklaces Lkj are ordered within Rk so that the first necklace Lk1 is always the the full necklace containing node 1k0n-k.
- We say that a necklace Lkj, k>= 2, can hook on necklace L(k-1)j' if
- L(k-1)j' is a full necklace
- in Lkj, there is a node w that can be converted into a node w' of L(k-1)j' by flipping one of its k 1's to zero. We say that w hooks on w'.
Since necklaces are closed under one-bit rotation and L(k-1)j' is a full necklace, any node in Lkj can then hook on a node of L(k-1)j'.
- Lemma: Any necklace Lkj can hook on some full necklace L(k-1)j'.
Take any win Lkj and let \alpha be the longest sequence of zero bits in w (including wrap-arounds). Let w' be the string obtained from w by inverting the bit 1 immediately to the right of \alpha. Since w' contains a unique longest substring of zero bits, it is aperiodic and the necklace containing w' has n nodes, so that it can be used as a hook necklace for Lkj.
- Our aim is to arrange the ordered list of all 2n-1 nonzero nodes of Qn into a table of [(2n-1)/n] rows of n nodes so that column i of this table contains all nodes of Di.
- initially, take any rotation of L11 and place it into the first row of the table,
- then for all k=2,3,..,n-1, take sequentially necklaces Lk1, Lk2,...
- find for Lkj its hook necklace L(k-1)j' in Rk-1,
- rotate Lkj so that the first node in Lkj hook to the node of L(k-1)j' which is in the column where we start to fill the table with nodes from Lkj.
Table shows the partitioning of nodes of Q6, the strings in column i represent the nodes of subtree Di, i in {0,..,n-1}. Figure shows the optimal OAS tree in Q4.
|
D0 | D1 | D2 | D3 | D4 | D5
| |
|
|
L11: {000001 | 000010 | 000100 | 001000 | 010000 | 100000}
| |
L21: {000011 | 000110 | 001100 | 011000 | 110000 | 100001}
| |
L22: {000101 | 001010 | 010100 | 101000 | 010001 | 100010}
| |
L23: {001001 | 010010 | 100100} | L31: {111000 | 110001 | 100011
| |
000111 | 001110 | 011100} | L32: {011001 | 110010 | 100101
| |
001011 | 010110 | 101100} | L33: {101001 | 010011 | 100110
| |
001101 | 011010 | 110100} | L34: {101010 | 010101} | L41: {100111
| |
001111 | 011110 | 111100 | 111001 | 110011} | L42: {101110
| |
011101 | 111010 | 110101 | 101011 | 010111} | L43: {101101
| |
011011 | 110110} | L51: {111110 | 111101 | 111011 | 110111
| |
101111 | 011111} | L61: {111111} |
|
CAPTION: Partitioning nodes of Q6 into equally-sized subtrees of an optimal OAS tree.
In 1-port SF hypercube, the source just injects packets one-by-one alternatively into all subtrees using the farthest-first rule. The same tree can also be used for WH hypercube, in particular in combination with all-port model: two paths in two different subtrees Di are vertex-disjoint.
CAPTION: An example of an optimal OAS tree in all-port SF noncombining Q4.
Combining model
Meshes and tori
The algorithms are basically the same as for OAB, except that the amount of data disseminated from the source changes during the communication. So, pipelining is used in case of SF switching and recursive doubling in case of WH switching.
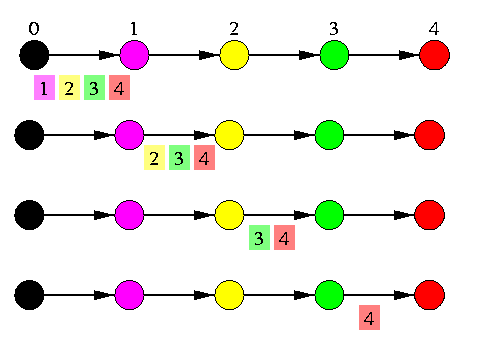
CAPTION: Nonoptimal OAS in 1-D SF torus using combining.
It is interesting to observe that combining is counterproductive in case of 1-D SF tori and meshes. The number of rounds is the same as in the noncombining OAS with farthest-first scheduling, but in combining (see Figure ), nodes transmit more data and the communication latency is worse compared to trivial pipelining, even if we ignore the overhead of packet combining. This algorithm is only used in an optimal AAS on 1-D torus.
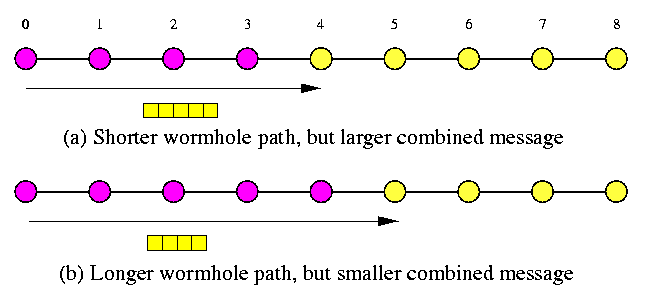
CAPTION: A tradeoff between the lengths of wormhole paths and message sizes in recursive doubling OAS on a WH 1-D mesh of size not equal to the power of two.
On the other hand, combining provides faster OAS in WH networks due to recursive doubling. We should only be careful with recursive splitting of linear paths/cycles in case their sizes are not powers of two, since the size of combined message depends on that. Figure illustrates the tradeoff.
An approximate formula for OAS latency in T(z) is
tOAS(T(z),M)=\sumi=1[log z](ts+[z/2i] td+M[z/2i] tm)=ts[log z] + (td+Mtm)({z}-1).
This is less than the communication latency in noncombining store-and-forward T(z), which is (ts+td+mtm)(z-1).
Hypercube
The communication pattern is again a SF spanning binomial tree and neither all-port capability neither WH switching make any difference. Figure shows an example for n=3. The labeling of hypercube arcs by (k)[i-j] denotes a transmission in round k of combined packets for nodes i-j. The total time is
tOAS(Qn,M)=\sumi=1n(ts+M2n-itm)=tsn + Mtm(2n-1)
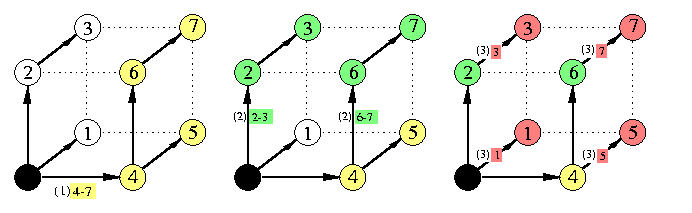
CAPTION: 3-round OAS in a combining 1-port hypercube Q3.
|











