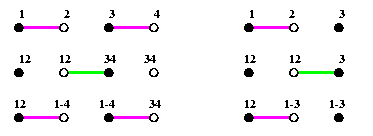Section#13: All-to-all broadcast algorithms in SF networks
(CS838: Topics in parallel computing, CS1221, Tue, Mar 16, 1999, 8:00-9:15 a.m.)
The contents
- SF switching with packet combining
- All-port full-duplex model
- All-port half-duplex model
- 1-port full-duplex model
- 1-port half-duplex model
- SF switching with no packet combining
- All-port full-duplex model
- All-port half-duplex model
- 1-port full-duplex model
- 1-port half-duplex model
In all-to-all broadcast, also called gossip or total exchange, every node sends the same packet to every other node. It is used as a subroutine in many important parallel algorithms.
The complexity of AAB depends strongly on parameters of the communication subsystem and on the packet size. If packets are small, then the number of rounds should be minimized, using combining of packets. If packets are large, then a SF noncombining approach where packets are pipelined separately across the network is the best. In this section, we will explain the AAB algorithms with SF switching in both combining and noncombining cases.
SF switching with packet combining
All-port full-duplex model
In this most powerful and least realistic model, the AAB can be performed optimally using again a kind of trivial flooding (or greedy) approach. The number of rounds to complete an AAB on any network G is diam(G). In the first round, every node sends its broadcast packet to all its neighbors and in further rounds, it simply keeps sending all the new packets he received to all its neighbors. This protocol is clearly inefficient and produces a lot of redundant packets sent around the network. The redundancy can be decreased by constraining some parameters.
All-port half-duplex model
Since half-duplex channels can simulate full-duplex channels with slowdown two, the trivial upper bound on the number of rounds with half-duplex channels is 2diam(G).
A trivial AAB scheme under these conditions is called gather-scatter. One node accumulates all the packets and then broadcasts the accumulated information in one aggregate packet using OAB. The number of rounds is bounded by the complexity of OAB.
But in many cases, we can do better.
Lemma
Assume all-port half-duplex combining model. If G is bipartite with diam(G)=D, then tAAB(G)<= D+1.
Proof
Since G is bipartite, it has a vertex 2-coloring. The AAB algorithm alternates odd-numbered rounds in which white nodes send information to black ones, with even-numbered rounds when the communication goes in the opposite way. Since black nodes start to disseminate the information in the second round, diam(G)+1 rounds are needed in the worst case.
CAPTION: AAB in a bipartite all-port half-duplex network.
Figure shows odd-numbered and even-numbered round in a bipartite network.
Similarly, orientation of edges of G may help. If G is an undirected connected graph and we assign orientation to every edge, we get a digraph \vec{G} which had an oriented diameter D'. If there is an oriented path from x to y for any two nodes x and y, then \vec{G} is strongly oriented and the oriented diameter is finite.
Lemma
Assume all-port half-duplex combining model. If diam(G)=D and diam(\vec{G})=D', then
D<= tAAB(G)<= min(2D,D')
Proof
The lower bound is always the diameter. The upper-bound 2D follows from the simulation of full-duplex channels by half-duplex ones with slowdown 2. But if AAB uses channels only in the direction implied by the orientation of \vec{G}, i.e., nodes just keep sending all the information they got form input channels to all output channels, then the number of rounds is D'.
The problem of enforcing orientation on edges of a graph so that the oriented diameter is minimum is hard in general. It has been solved for 2-D meshes and tori, for some higher-dimensional meshes and tori, and for hypercubes. All these topologies have orientation with diameter equal or nearly equal to the unoriented diameter. In case of 2-D meshes, it is also called the Manhattan problem: Make the streets and avenues in Manhattan one-way so that the distances remain the same as before. The constructional proof of the Manhattan problem is very long and technical. The problem is trivial for de Bruijn and Kautz digraphs.
Here, we will show only the proof for the hypercube. The orientation is again constructed inductively. It follows from a more general construction.
Lemma
If a bipartite graph G has an orientation of diameter <= k, k>= 3, such that every vertex is in a cycle of length <= k, then graph G× K2, the cartesian product of G and the complete graph on two vertices, has an orientation of diameter <= k+1 such that every vertex is in a cycle of length <= k.
Proof
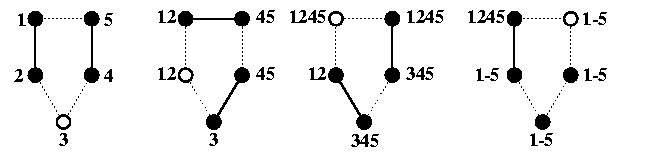
Constructive. Take two copies of G, G1 and G2, with 2-coloring of vertices, assume black and white, and make G× K2 by joining every vertex in G1 with its image in G2. The orientation of edges of this perfect matching is
from G1 to G2 iff the incident vertices are black ( Figure (a)).
Cartesian product preserves the length of oriented cycles in both copies, so that the induction hypothesis is preserved. We will distinguish only four cases, the other ones are symmetric.
- By induction, there is a path of length at most k+1 from any black vertex u in G1 to any vertex v in G2 (go to u', the image of u in G2, and use induction to get from u' to v) ( Figure (b)).
- By induction, there is a path of length at most k+1 from any black vertex u in G2 to any white vertex v in G1 (use induction to get to v', the image of v in G2, and go to G1) ( Figure (c)).
- There is a path of length at most k+1 from any black vertex u in G2 to any black v vertex in G1.
- If v is the image of u, then the path from u to its successor w in a cycle C\subset G2 of length <= k, to the image of w in G1, and then to v using the image of C in G1 has length 2+(k-1) ( Figure (d)).
- If v is not the image of u, let v' be its image in G2. Then there is a oriented path from u to v' of length at most k in G2. Let w be the vertex adjacent to v' on this path and let w' be its image in G1. Then the path from u to v via w and w' has the length <= (k-1)+2 ( Figure (e)).
To make the graph G× K2 bipartite, just flip the colors in one of its halves.
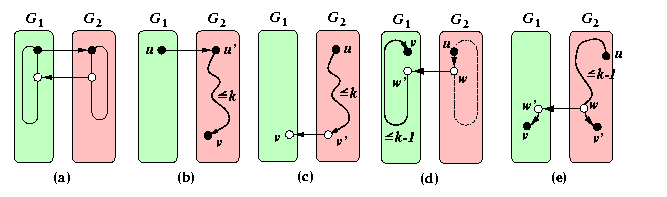
CAPTION: Induction step of orientation of graph G× K2.
The result for the hypercube follows from the fact that diam(\vec{Q}2)=3, diam(\vec{Q}3)=5, and diam(\vec{Q}4)=4 (see Figure ).
Corollary
For n>= 4, diam(\vec{Q}n)=n.
CAPTION: The oriented diameter of Q4 is 4.
1-port full-duplex model
Also here, we can apply 1-port gather/scatter. Since in the combining model, the complexity of the gather operation is the bounded by the complexity of the broadcast, we have
Lemma
For any N-node graph G,
max(diam(G),[log N])<= tOAB(G)<= tAAB(G)<= 2tOAB(G)
Note that we do not need full-duplex channels for this approach. However, for some topologies, there are much faster AAB algorithms, close to the lower bound max(diam(G),[log N]).
Lemma
Assume full-duplex 1-port combining model. Then the number of rounds of AAB on mesh-based topologies is the following.
- tAAB(M(z))=
{z-1 if z is even,
z otherwise.
}
- tAAB(T(z))=
{z/2 if z is even,
(z+3)/2 otherwise.
}
- tAAB(M(z1,...,zn))=\sumi=1n tAAB(M(zi)), tAAB(T(z1,...,zn))=\sumi=1n tAAB(T(zi)).
- tAAB(Qn)=n.
Proof
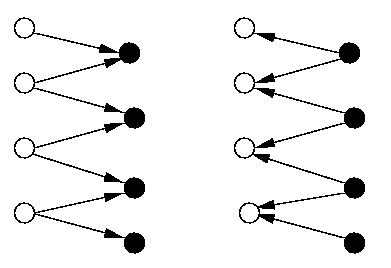
- Consider linear array M(z) of nodes i, i=1,...,z. The algorithm alternates odd-numbered rounds and even-numbered rounds, starting from round 1.
- In odd-numbered rounds, the exchange of information is between all odd-even pairs of nodes, i.e., between 1 and 2, 3 and 4, and so on.
- In even-numbered rounds, the exchange of information is between all even-odd pairs of nodes, i.e., between 2 and 3, 4 and 5, and so on.
The result is by a simple case analysis. See Figure for an example.
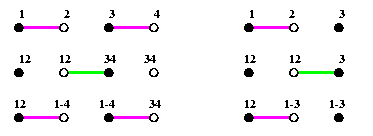
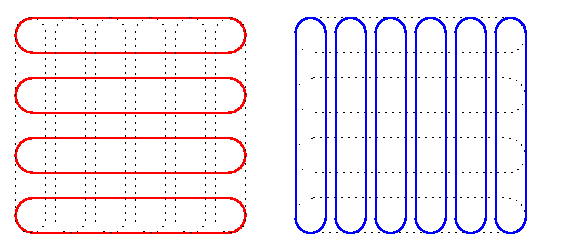
CAPTION: AAB on a full-duplex 1-port combining linear array.
- 1-D tori T(z) are treated exactly the same way.
- z is even. Then these odd-even and even-odd pairs form always a perfect matching. Every packet proceeds by one hop in both directions in each round from its original source. The number of rounds equals the diameter.
- z is odd. Then always one node is out of game. This requires two more rounds than the diameter is. Figure gives the idea of an optimal schedule..
CAPTION: AAB on a 1-port full-duplex cycle of length 5 in 4 rounds.
- AAB on higher-dimensional 1-port meshes and tori can be performed by using the cartesian-product property. All the nodes exchange information along dimension 1 so that each of them knows the accumulated information for the whole linear array/cycle corresponding to dimension 1. Then the exchange proceeds along second dimension so that nodes belonging to the same 2-D submesh/subtorus are mutually informed. And so forth. Since the overhead with combining the information together is ignored, the total number of rounds is just a plain sum of rounds of these phases.
CAPTION: Dimension-ordered AAB in 1-port full-duplex 2-D tori.
- The algorithm is in fact a special case of that for meshes/tori. In round i, i=0,...,n-1, the communication proceeds along all channels in dimension i which induces n edge-disjoint perfect matchings. 1-port hypercube algorithm is optimal, the number of rounds matches the diameter, and all-port assumption does not improve anything.
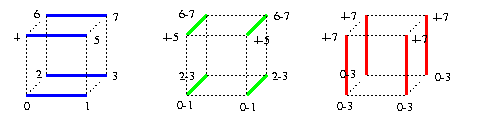
CAPTION: 3-round AAB in 1-port combining hypercubes. The node labels correspond to the information so far received by that node.
The size of messages doubles each round and so
tAAB(Qn)=\sumi=0n-1(ts+2iMtm)=tsn+Mtm(2n-1)
The first term is a product of the diameter and startup time, the second term is the product of the number of nodes and one-hop inter-router latency.
1-port half-duplex model
The AAB algorithms for half-duplex mesh-based topologies are very similar to those for meshes with full-duplex channels.
The best thing to do for linear arrays is to simulate full-duplex channels by alternating the direction of communication on half-duplex channels, the number of rounds just doubles ( Figure ).
For 1-D torus T(z), we may use a similar approach, but surprisingly, this does not give optimal results. There is a better solution which is embarrassingly trivial:
pipeline all packets around the cycle in one direction.
The number of rounds is always z-1, for both even and odd z. All the channels are used in all rounds which may intuitively explain better efficiency compared to simulation of full-duplex exchanges.
Algorithms for higher-dimensional meshes/tori and hypercubes can be again derived from these basic ones using cartesian-product property, similar to the approach shown on Figure . Consider 2-D torus T(z,z) whose every node holds initially a packet of size M. In the first phase, each node collects packets within its horizontal cycle and ends up with a packet of size zM. In the second phase, every node participates in an AAB within its vertical cycle. Since all the communication is neighbor-neighbor, we may omit the internode latency td and the total time becomes
tAAB(T(z,z))=(ts+mtm)(z-1)+(ts+zmtm)(z-1)=2ts(z-1)+mtm(z2-1)
This trivial solution can be generalized to arbitrary meshes or tori, but it is not optimal. Optimal solutions are known, however, they are more complicated. Figure gives just an idea of an optimal strategy for 2-D tori.
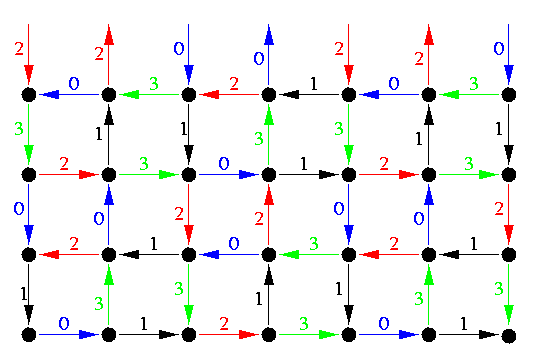
CAPTION: The basic pattern for AAB in a SF 1-port half-duplex 2-D tori, based on repeating matching patterns 0, 1, 2, and 3.
SF switching with no packet combining
All-port full-duplex model
Each of N input packets must be delivered individually to all nodes. The number of packets moving in parallel across the network is much higher than in the combining model. Full-duplex channels are pairs of inverse simplex links, called arcs. Every node u of network G is the root of a broadcast spanning tree B(u). Each arch of B(u) is labelled with the number of the round in which the broadcast packet passes this arc. An arc with label i is said to be of level i. The height of B(u)), h(B(u)), is the highest arc label in B(u). Two trees B(u) and B(v) are said to be time-arc-disjoint if for any i in {0,...,min(h(B(u)),h(B(v)))-1}, the sets of arcs at level i in B(u) and B(v) are disjoint.
The motivation behind these definitions follows from the lock-step assumption: all the nodes start their broadcasts at the same time and the broadcasts proceed synchronously along the trees with same speed. At round i, only the arcs at level i are active in all the trees. If broadcast trees are time-arc-disjoint, then all these parallel broadcasts are pairwise link-contention-free.
The lower bound on the number of rounds in network G with N nodes and minimum degree d is [(N-1)/d]. Hence, it is [(z1z2-1)/2] for M(z1,z2), [(z1z2-1)/4] for T(z1,z2), [(2n-1)/n] for Qn, and so on.
Under these assumptions, the problem of designing an optimal AAB algorithm reduces to the problem of designing TADBTs rooted in every node of the network! Here, we can nicely demonstrate how important is the symmetry of the underlying topology for solving such a problem. If the topology is vertex-symmetric, we may have a chance to find a generic structure of a TADBT, independent of the location of its root. This problem has been solved for 2-D and 3-D tori, 2-D meshes, hypercubes, and some other Cayley graphs.
2-D tori
2-D tori are vertex-symmetric. The broadcast trees can be made isomorphic to each other, being translations of a generic tree, denoted B(*). The translation from node u to v of T(z1,z2) is an automorphism piu-> v of T(z1,z2) defined by
piu-> v: x-> x+ v- u
where + and - denote coordinate-wise addition and subtraction modulo z1 and z2. The translation preserves all the arc labels (i.e., arc time levels). It is easy to show that
Lemma
The broadcast trees made by translations of B(*) are pairwise TADBTs iff all the arcs at each level i in B(*) are of distinct directions.
In T(z1,z2) there exist four directions N,E,W,S. It follows that B(*) provides an optimal AAB in T(z1,z2) iff
- each level of B(*) consists of at most 4 arcs of distinct directions from the set {N,E,W,S}.
- h(B(*))=[(z1z2-1)/u]
The structure of such a tree is trivial if z1=z2 is odd. The B(*) consists of 4 snakes of size (z1z2-1)/4, which are rotations of the same pattern and which cover completely the whole torus. Figure shows two solutions.
The AAB in such a torus is also memory optimal. Routers need no auxiliary buffers for storing packets: every packet is stored into the local-node memory and forwarded to one of output channels.
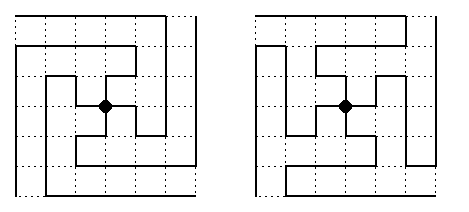
CAPTION: Two different TADBTs in T(7,7). The wrap-around torus edges are omitted.
Time- and memory-optimal solutions exist for any 2-D and 3-D torus. in 2-D case, a general T(z1,z2) requires \beta<= 3, but in many cases, there is even a buffer-less time-optimal AAB, Figure shows a simple example.
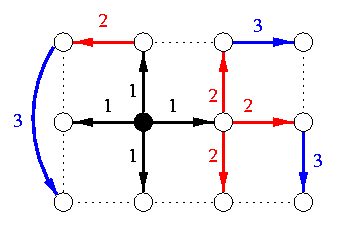
CAPTION: An example of generic broadcast tree for a bufferless AAB in all-port noncombining T(3,4).
A trivial solution exists for AAB in 3-D cube T(z,z,z) if z is odd. The cube is partitioned into 6 pyramids, covered by isomorphic snakes. In general 3-D T(z1,z2,z3) requires \beta<= 60.
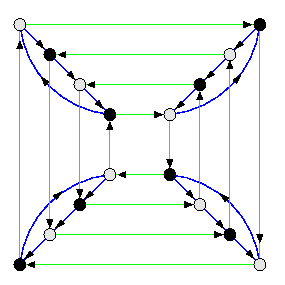
Hypercube
The same approach can be used in hypercubes, since Lemma can be easily generalized to any vertex-symmetric mesh-based topology. We need to build a generic broadcast tree B(*) of Qn such that the set of arcs at level i consists of n hypercube arcs of n distinct directions, except for the last level m=[(2n-1)/n] which consists always of less than n arcs (due to small Fermat theorem, 2n-1 is not divisible by n). Then the number of rounds will match the lower bound.
Similarly to the construction of the OAS tree in Section #12, without loss of generality, we can place the root of the generic tree into node 0n and the construction of B(0n) is based on partitioning the nodes of Qn into necklaces and on arranging the nodes into an n-column table. In contrast to the OAS tree where each column consisted exclusively of nodes of one subtree of the OAS tree, here the requirement of time-arc-disjointedness implies that
- row i of the table defines the tree nodes at level i (i.e., informed in round i),
- if node u=un-1... u0 appears in column j, j=0,...,n-1, then uj=1,
- the AAB tree is constructed by connecting every node u=un-1... uj+11uj-1... u0 in column j to node \nonj(u)=un-1... uj+10uj-1... u0 (which is never in the same column as u).
The last condition implies that all input arcs of nodes on a given level have distinct directions. To make this possible, the arrangement of nodes into such an n-column table must guarantee that
- if u is in column j, j=0,...,n-1, then node \nonj(u) appears at an earlier level (= row) than node u.
The construction is the following:
- All nonzero nodes are partitioned into equivalence classes Rk, 1<= k<= n-1, consisting of nodes with k 1's, listed in ascending order of the number of 1's in their nodes: R1,...,Rn-1,Rn.
- Each Rk is split into necklaces Lkj, closed with respect to left rotation. Depending on the periodicity of nodes, each necklace consists of q nodes, where q=n (full necklaces) or q < n is a divisor of n (degenerate necklace).
- Necklaces Lkj are ordered within Rk so that the first necklace Lk1 is always the the full necklace containing node 1k0n-k. The remaining necklaces in each Rk can be taken in any order.
- Starting with L11, we take necklaces in the order above and fill with their nodes the n-column table row-wise left-to-right so that each necklace which fills the table from column j is always rotated so as to start with a node u which has uj=1. It can be any such node of the necklace except for necklaces Lk1, where the first node must have at position j-1 (cyclically) zero bit. This condition is sufficient for meeting the requirement that node \nonj(u) is at a higher row in the table than node u, where j is the column of u.
Table shows one such partition of V(Q6) into a 6-column table. For example, the first necklace of R4, L41, starts in column 5 and therefore it must start with node u such that u5=1 and u4=0. The only node in this necklace with this property is node u=100111.
|
|
|
| {0} | {1} | {2} | {3} | {4} | {5}
|
|
|
|
1 | L11{:} {000001 | 000010 | 000100 | 001000 | 010000 | 100000}
|
|
2 | L21{:} {000011 | 000110 | 001100 | 011000 | 110000 | 100001}
|
|
3 | L22{:} {010001 | 100010 | 000101 | 001010 | 010100 | 101000}
|
|
4 | L23{:} {001001 | 010010 | 100100} | L31{:} {111000 | 110001 | 100011
|
|
5 | 000111 | 001110 | 011100} | L32{:} {101100 | 011001 | 110010
|
|
6 | 100101 | 001011 | 010110} | L33{:} {001101 | 011010 | 110100
|
|
7 | 101001 | 010011 | 100110} | L34{:} {101010 | 010101} | L41{:} {100111
|
|
8 | 001111 | 011110 | 111100 | 111001 | 110011} | L42{:} {111010
|
|
9 | 110101 | 101011 | 010111 | 101110 | 011101} | L43{:} {110110
|
|
10 | 101101 | 011011} | L51{:} {111101 | 111011 | 110111 | 101111
|
|
11 | 011111 | 111110} | L61{:} {111111} | | |
|
|
|
|
|
CAPTION: Partition of V(Q6) into a 6-column 11-row table. Every node u in row k and column j can be connected to a node \nonj(u) which always appears in row l, l < k.
Figure shows in detail the structure of the corresponding broadcast tree B(06) of height 11.

CAPTION: A time-arc-disjoint spanning tree of Q6.
Time-independent gossip in symmetric networks
The AAB algorithms based on TADBTs enforce time-dependent behavior on nodes:
the routing function depends on the round number. If the topology is node- and edge-symmetric and the degree of nodes is even, say 2d, then we can decompose the arc set into d arc-disjoint hamiltonian cycles. This allows a fixed routing function in every node during the whole AAB. The advantage of this solution is that it is always bufferless and it was generalized to any hamiltonian higher-dimensional torus, the disadvantage is that it cannot be time-optimal if every node has initially only one packet.
Lemma
Consider a network G with degree 4. A time-independent AAB algorithm on 2 edge-disjoint hamiltonian cycles with one packet per node requires at least [11N/40-1] rounds.
On the other hand, AAB on a 2-D torus where every node initially holds 2 packets becomes time-optimal. The solution is easy in case of even-sized tori.
Lemma
If every node in T(z1,z2) with z1,z2 even holds initially 2 packets, then there is a time-independent AAB in z1z2/2 rounds.
Proof
Every node just sends packet 1 (2) to both directions along hamiltonian cycle 1 (2), respectively. Every packet makes z1z2/2 hops to reach all other processors. Every node receives 4 packets in every round and stores them into the local node memory. If c(u) denotes the column number of node u, then node u implements the following routing function for forwarding packets from input to output channels:
- N <-> E and S <-> W, if c(u)=z2-1 or c(u) is even,
- N <-> W and S <-> E otherwise (see Figure ).
Only in the last round, each node receives twice the same packet.
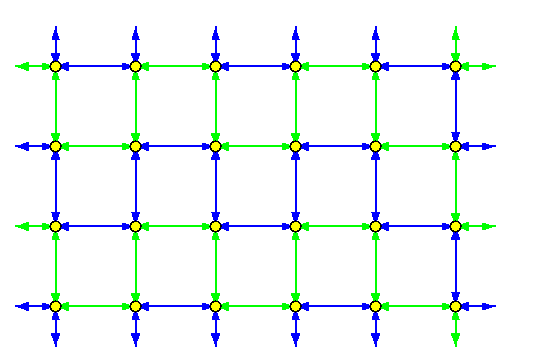
CAPTION: Two edge-disjoint hamiltonian cycles in T(4,6).
All-port half-duplex model
Again, we can simulate full-duplex AABs by doubling the number of step, which however in most cases does not provide optimal solutions. Here we will show an asymptotically time-optimal AAB algorithm for 2-D meshes which unfortunately is not memory-optimal, it requires \beta=\sqrt{N} for an N-node mesh. It consists of two phases. Let us define it for simplicity only for square meshes M(z,z) where z is even, since generalization to other 2-D meshes is obvious.
- Apply 2-coloring to partition nodes of T(z,z) into blue and green ones (see Figure ).
- Every blue (green) node holds a blue (green) packet.
- Phase 1: Blue nodes perform AABs of blue packets within rows and simultaneously green nodes perform AABs of green packets within columns. Blue nodes only store green packets and green nodes only store blue packets.
- The AABs take just z-1 rounds, since there is no contention on half-duplex links.
- At the end of Phase 1, every node holds all z/2 blue packets from its row and all z/2 green packets from its column (see Figure ).
- Phase 2: All nodes perform row AABs of green packets and simultaneously column AABs of blue packets. These AABs consist of two parts:
- the first part is a trivial half-duplex simulation of full-duplex all-port exchanges until the latest packet moving leftward passes the latest packet moving right in the middle of each row or column. If z is even, the full-duplex scheme would take z/2 steps, each consisting of z/2 rounds, so this half-duplex simulation takes z2/2 rounds (see Figure (c)).
- the second part is just a straightforward pipelining of both packet waves towards the borders, which takes 2(z/2-1) rounds (see Figure (d)).
Phase 2 takes therefore z2/2+n-2 rounds.
The lower bound on the number of rounds is the ratio of z2(z2-1), the total number of hops that must be performed, and 2(z2-z), the maximum number of hops per one round which M(z,z) can provide, i.e., (z2+z)/2. This algorithm is therefore asymptotically optimal.
CAPTION: All-port half-duplex AAB in noncombining M(4,4) (a) Initial 2-coloring. (b) Distribution of packets after Phase 1. (c) The first two steps of Phase 2 in the first row of the mesh. (d) The first row after the first part of Phase 2.
1-port full-duplex model
In this model, each node can only exchange exactly one packet with one of its neighbors. Several lower bounds apply here.
Lemma
For N-node network G, the lower bound on the number of rounds of AAB, g(G), is
[ {N(N-1)/ 2\mu(G)}]
where \mu(G) is the size of maximum matching in G.
Since for any N-node graph G, \mu(G)<=[ N/2], we have
Corollary
g(G)>= N-1.
Any hamiltonian graph can achieve this lower bound by alternating even-odd and odd-even pair exchanges between nodes along its hamiltonian cycle. It is similar solution to that in Figure .
Lemma
For N-node network G=(V,E), let X\subset V be a vertex cutset of G whose removal disconnects G into the q connected components Vi. The the lower bound on the number of rounds of AAB is
[ \sumi=1q{max(|Vi|,N-|Vi|)/|MX|}],
where MX is the maximum matching in joining X with VX.
Proof
For each i=1,...,q, X must intermediate at least N-|Vi| packets to inform Vi from V-Vi, and inversely, X must intermediate at least |Vi| packets to inform V-Vi from Vi, so at least max(|Vi|,N-|Vi|) packet must be relayed between Vi and X. Since X is shared by all components, at least \sumi=1qmax(|Vi|,N-|Vi|) packet transmissions are needed between nodes of X and nodes of VX=\cupi Vi.
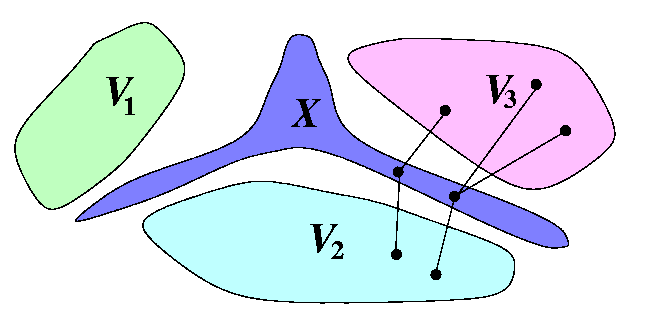
CAPTION: Lower bound on the number of rounds in 1-port full-duplex noncombining AAB
1-port half-duplex model
Optimal or nearly optimal AAB algorithms are known for this weakest model, where every node can either send or receive one packet in one round. Since most parallel machines have more powerful communication capabilities and the optimal or nearly optimal solutions known for mesh-based topologies are fairly complicated, we skip this part here.