Section#16: Asymptotically optimal mesh sorting algorithm
(CS838: Topics in parallel computing, CS1221, Thu, Mar 25, 1999, 8:00-9:15 a.m.)
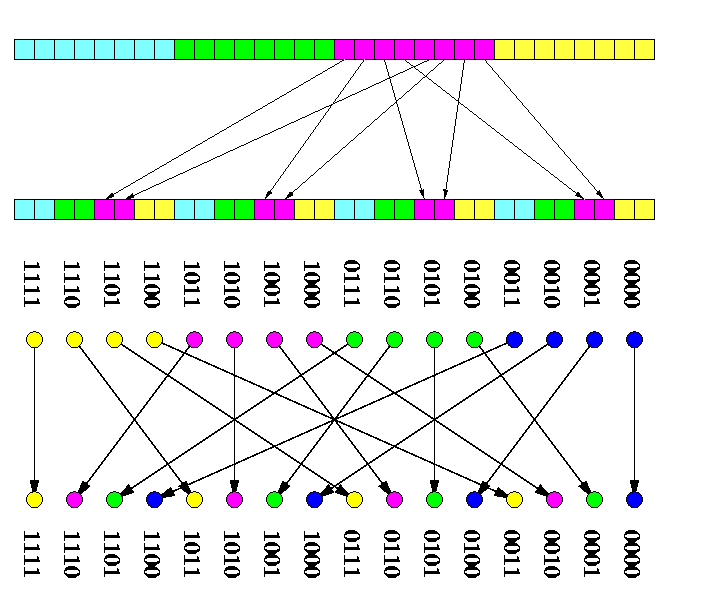
Let N=n2. Consider M(n,n) of N nodes, each holding a number. Divide the mesh into n1/2 submeshes M(n3/4,n3/4), called shortly blocks. One column of n1/4 blocks is called a vertical slice and one row of n1/4 blocks a horizontal slice. Let m=n1/4 be the # of blocks in one slice (horizontal or vertical). Block (i,j) is the block in the i-th horizontal slice and j-th vertical slice.
The algorithm consists of 8 phases:
Lemma
The algorithm sorts N=n2 numbers on mesh M(n,n) into a snake-like order in
3n+o(n)
parallel steps.
Proof
(by 0-1 Sorting Lemma)
- Every horizontal slice consists of m blocks and every vertical slice consists of m blocks.
- After Phase 1, each block contains at most one dirty row (see Figure ).
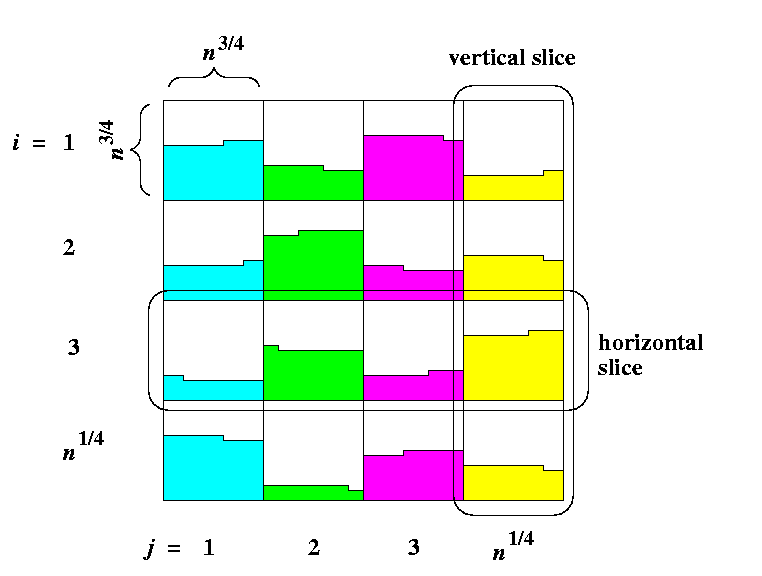
CAPTION: The situation after Phase 1.
- In Phase 2, all potential m dirty rows in each horizontal slice are uniformly distributed among all blocks of the slice. In the worst case, all such dirty rows may have the 1's starting at the same position modulo m in each block and so after the permutation one block can get by at most m 1's more than another one. Hence, after Phase 2, any two blocks within each horizontal slice can differ by at most m 1's.
- It follows that the number of 1's between any two vertical slices can differ by at most n1/2= m2 1's.
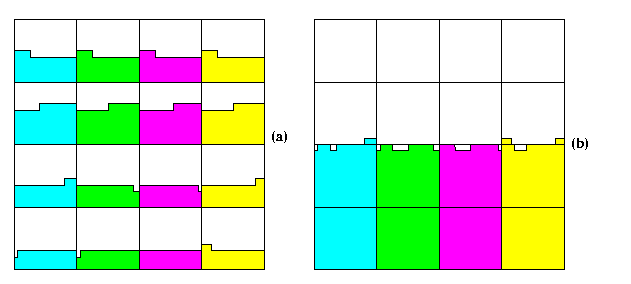
CAPTION: The situation after (a) Phase 3 and (b) Phase 4.
- Since any two blocks within one horizontal slice can differ by at most m 1's and the length of one row in each block is n3/4=m3, it follows that after Phase 3, each horizontal slice can have at most 2 dirty rows (see Figure (a)).
- After Phase 4, each vertical slice can have at most m dirty rows, since it consists of m blocks, each with at most one dirty row (see Figure (b)).
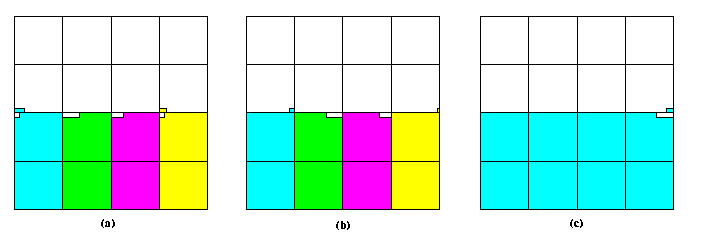
CAPTION: The situation after (a) Phase 5 and (b) Phase 6.
- Those m dirty rows can span the boundary between even-odd or odd-even pairs of vertically adjacent blocks (as shown for example in Figure (b)), therefore we need both Phase 5 and 6 (see Figure ).
- After Phase 6, each vertical slice can have at most one dirty row (see Figure (b)).
- We know that any 2 vertical slices can differ in at most n1/2 1's. Since the rows in vertical slices have length n3/4 > n1/2, there can exist at most 2 global dirty rows in M(n,n) and the number of 1's in them can differ by at most n1/2× m=n3/4.
- After Phase 7, if just one dirty line remains, we are done (as in our example).
- If there are still 2 dirty lines, the upper one consists of 0's except perhaps for at most n3/4 1's and the lower one consists of 1's except perhaps for at most n3/4 0's.
- Then Phase 8 must complete the sorting.
Proof of the parallel time complexity: Each block is mesh M(n3/4,n3/4). If we use Shearsort within blocks and even-odd transposition in rows and columns, we have
- Phase 1: T1(N)=n3/4(2log n3/4+1)=O(n3/4log n)
- Phase 2: T2(N)=n
- Phase 3: T3(N)=T3(N)
- Phase 4: T4(N)=n
- Phase 5: T5(N)=O(n3/4log n)
- Phase 6: T6(N)=T5(N)
- Phase 7: T7(N)=n
- Phase 8: T8(N)=2n3/4
Hence the total parallel time complexity is \sumi=18 Ti(N)=3n+O(n3/4log n)=3n+o(n).