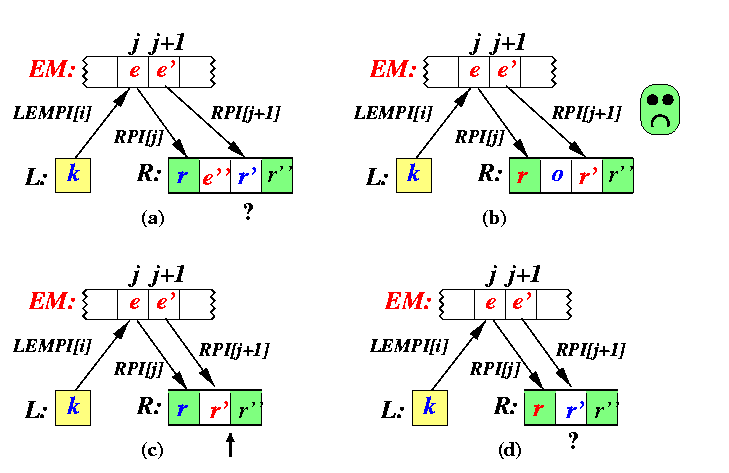Section#18: Cost-optimal EREW PRAM sort
(CS838: Topics in parallel computing, CS1221, Thu, Apr 1, 1999, 8:00-9:15 a.m.)

1. Standard Even-Even Merge Sort on EREW PRAM
2. Cost- and time-optimal merge operation on EREW PRAM
3. Proof of correctness of the cost-optimal merge operation
4. Complexity of Cole's EREW PRAM Merge Sort

Back to the beginning of the page	Back to the CS838 class schedule

Standard Even-Even Merge Sort on EREW PRAM

Lemma

Let N=2^k and L[1,...,N] and R[1,...,N] be two monotonically ordered sequences.
Let Z={EEMerge}(L,R) be the resulting merged sequence of length 2N.
Then

Z={Pairwise_CE}({Even_Odd_Interleave}(OM,EM))

where EM[1,...,N]={EEMerge}(even(L),even(R)) and
OM[1,...,N]={EEMerge}(odd(L),odd(R)).

CAPTION: An illustration of the reasoning in the non-binary proof of correctness of the classical Even-Even Merge operation.

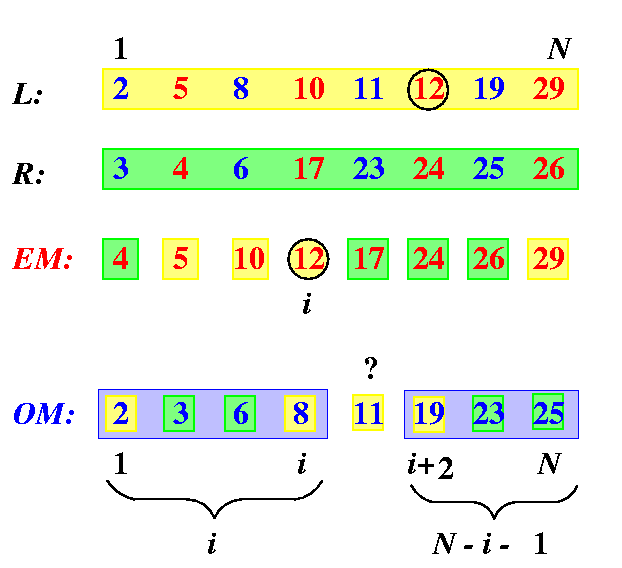
Consider any number z=EM[i], 1<= i<= N. Then

• every number EM[k], k<= i, comes from an even-numbered position in L or R. In its original sequence, it is therefore preceded by exactly one odd-position number which now appears somewhere in OM. It follows that all the numbers OM[1,...,i] must be < z.
• Except for 2 numbers (the last numbers in L and R), every number EM[k], k>= i, is followed in its original sequence by exactly one odd-position number, which now appears somewhere in OM and so (N-i+1)-2=N-i-1 numbers in OM must be greater than z, i.e., all the numbers OM[i+2,...,N] are > z.

Lemma

Let z=EM[i] be the number on i-th position in EM and let j be the original index of z in its original input sequence, say L (the statement for input sequence R is exactly the same). Hence, z=L[j]. Let f(z) be the final position of z in the final sequence Z. We claim that

2i<= f(z)<= 2i+1.

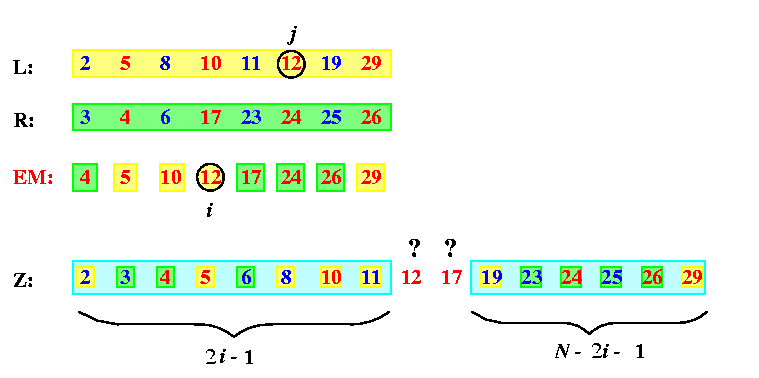
CAPTION: An illustration of the alternative proof of Even-Even Merge for N=8, z=12, i=4, and j=6.

Proof

• Out of i-1 numbers preceding z in EM, exactly j/2-1 come from L, and therefore i>= j/2.
• Obviously i-j/2 numbers preceding z in EM come from R and each of them is preceded by one number at odd position there.
• All together, the numbers which must precede z in Z are
  • all the j-1 numbers which have preceded it in L
  • plus all the i-j/2 odd-even pairs from R,
  which gives

  f(z) > j-1+2(i-j/2)=2i-1.
  

• Similarly, N-j numbers follow z in L.
• Out of N-i numbers following z in EM,
  • exactly N-i-(N-j)/2 must come from R and
  • each of them, except the last one, is followed in R by exactly one odd-position number larger than z.
• All together, z must be followed in Z by
  • N-j numbers from L
  • plus 2(N-i-(N-j)/2)-1 numbers from R,
  So we get that the last N_j+2(N-i-(N-j)/2)-1=2N-2i-1 numbers in Z, i.e., numbers Z[i+2,...,2N], must be greater than z, and so f(z)<= 2i+1.

Assume that we know only EM and we would like to determine the final positions in Z of numbers on odd positions, i.e., of numbers in L\cup R-EM, but without knowing the sequence OM, i.e., without performing the second merge merge operation. In general, it is impossible. See Figure for a typical situation.

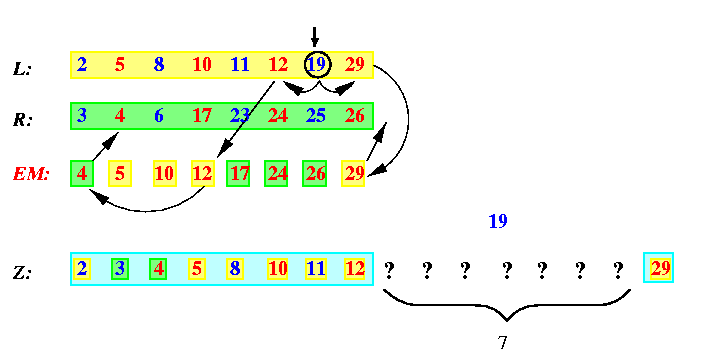
CAPTION: Knowing only EM, we cannot decide final positions of numbers from L\cup R-EM in Z.

The number 19 in sequence L must be preceded in Z by 6 numbers for its original sequence L, but since its predecessor in L, number 12, is preceded in EM by only number 4 from R, we can be sure about only two predecessors from R of 19 in Z, numbers 3 and 4. Since the successor of 19 in L, number 29, is the last number in EM, we do not know at all which numbers from R must follow 19 in Z. Hence, 19 can potentially end up on any of 7 undecided positions in Z.

But it turns out that with some additional O(N) computation, we can determine exactly the final positions of the odd-positioned numbers without performing the operation {EEMerge}(odd(A),odd(B)). And this is the main idea of the cost-optimal EREW PRAM MergeSort, which is also called Cole's merge sort: in each level of EEMS, to apply recursively only one even-even merge operation and perform some auxiliary O(N) computations to find the final position for all numbers in L\cup R. The idea of the auxiliary computation is to find for every number in xin L\cup R-EM the index of the largest yin EM such that y < x.

Then the number of CE operations for the merge operation of 2N numbers is given recurrently by equations

cm(2N) =  cm(N) + O(N)

cs(2N)=2 cs(N)+ cm(2N)=O(Nlog N).

Back to the beginning of the page	Back to the CS838 class schedule

Cost- and time-optimal merge operation on EREW PRAM

Back to the beginning of the page	Back to the CS838 class schedule

Proof of correctness of the cost-optimal merge operation

Lemma

The algorithm of EffMerge calculates correctly the final positions in Z of all numbers from L\cup R.

Phase A:

The proof is very similar to Lemma . Assume wlog that z=EM[i] has z.Origin=L. Let j=z.OrigIndex. Then z is preceded in EM by \alpha=j/2-1 numbers from L and the remaining \beta=i-1-\alpha=i-j/2 numbers are therefore from R, each of them preceded by an odd-position number there. Hence, z must be greater than 2\beta=2i-j numbers in R. At the same time, the number at the next even position in R, i.e., the number L[2i-j+2], must be greater than z, since it follows z in EM. So the only uncertain number in R w.r.t.~z is at position \gamma=2i-j+1. Figure shows the values in the array OpPI for our example above.

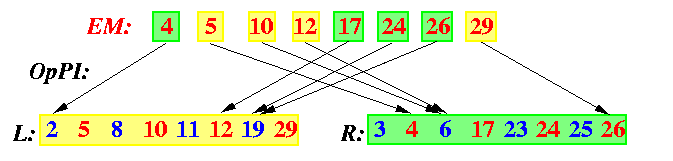
CAPTION: Array OpPI: the indexes of predecessors of numbers from EM in their opposite input sequences.

Phase B:

The aim is to make the names of predecessor indexes independent on the origin of z. The predecessor of z=EM[i] in L has simply index LPI[i] and the predecessor of z=EM[i] in R has index RPI[i].

Span of RPI and LPI:

Before we prove the rest, let us show a useful auxiliary statement on properties of indexes LPI and RPI, which basically means that adjacent LPI or RPI indexes are never more than 2 apart.

Proposition

For any i, 1<= i<= N, LPI[i+1]-LPI[i]<= 2 and the same for RPI.

Proof
Figure shows the only two possible cases if LPI[i+1]-LPI[i]=3. In both of them we can derive a contradiction, and the same contradiction appears if LPI[i+1]-LPI[i] > 3.

case (a):

Since LPI always points to the largest less number in L, we have e₁ < e<= o₁. But o₁ < e₂ < o₂ < e' and therefore e < e₂ < e'. And this is a contradiction with assumption that e and e' are adjacent numbers in EM with nothing in between.

case (b):

Similarly, o₁ < e<= e₁ < o₂ < e₂ < e' leads to e < e₂ < e'.

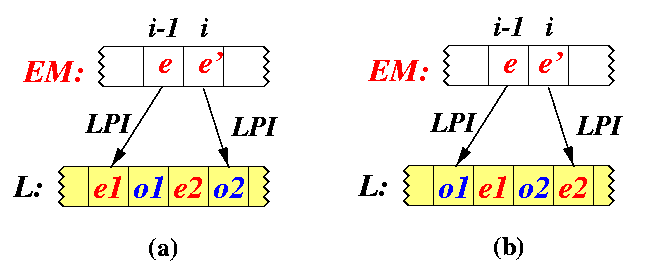
CAPTION: The maximal span between adjacent LPI or RPI is at most 2.

Phase C:

Let z=L[j], j odd, be a number in L-EM. It serves as a predecessor for at least one number in EM, but there may more numbers in EM, whose LPI points to z. Let e=EM[i] be the least (the leftmost) one among them. Then clearly LPI[i]\not =LPI[i-1] and e'=EM[i-1] must be less than z. But since e' precedes immediately e in EM, it is the greatest number in EM less than z. A detailed analysis reveals that only 2 different situations can appear and in both of them LEMPI[j]=i-1. Figure illustrates all cases.

case (a):

LPI[i-1]=j-1. Let x=L[j-1] and y=L[j+1] be the neighbors of z in L, both must appear in EM. Then x < e' < z < e<= y.

case (b):

LPI[i-1]=j-2. Let x=L[j-1] and y=L[j-2]. Then x must appear in EM. At the same time, e'<= x (since y < x and y is the greatest number in L less than e') and x < e (since x < z and z < e). So x must appear in EM before e, but not before e'. It is possible only if x=e' and then LEMPI[j]=i-1.

case (c):

This case cannot appear due to Proposition .

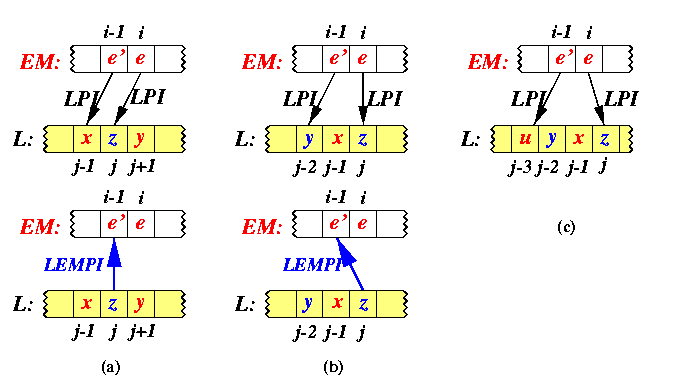
CAPTION: Calculation of indexes LEMPI.

The indexes in the array LEMPI and REMPI in our example are shown on Figure

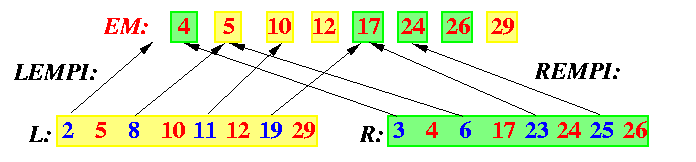
CAPTION: The indexes LEMPI and REMPI pointing to EM to predecessors of numbers from L-EM and R-EM.

Phase D:

We will give the proof only for case D2, since D1 is trivial and D3 is analogous to D2.

To compute the final position for numbers from L-EM, we must know for each of them how many numbers precede them in R. Consider any k=L[i], i is odd. Let j=LEMPI[i], e=EM[j], e'=EM[j+1], r=R[RPI[j]], r'=R[RPI[j+1]], and r''=R[RPI[j+1]+1]. Since k > e and e > r, we have k > r. Similarly, k<= e' and e'<= r'' implies k<= r''.

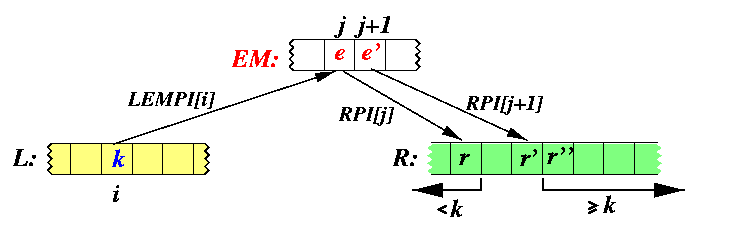
CAPTION: A generic situation for calculation of number of predecessors of numbers from L-EM in R.

From Proposition we know that the interval (r,r') can contain at most two numbers. A detailed analysis again reveals that among four possible cases, only two can really appear and the other two are handled by the algorithm. See Figure for all four situations.

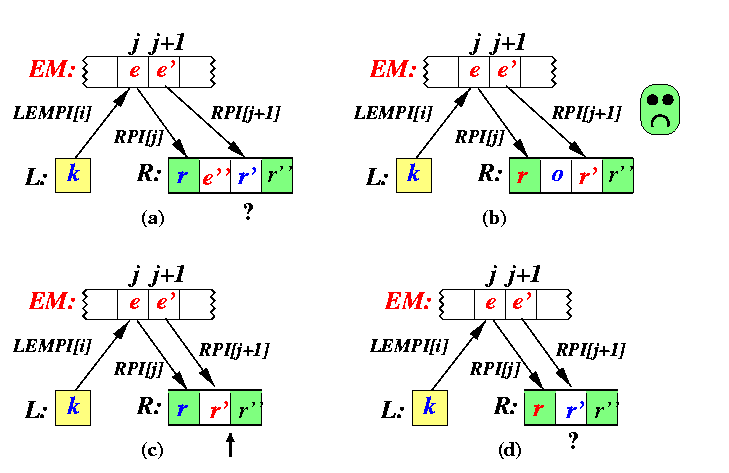
CAPTION: All cases for calculation of number of predecessors of numbers from L-EM in R.

case (a):

Both r and r' are 1 apart and are on odd positions. It follows that r < e'' < r' < e' and r < e < e' and r < e < k. Then e=e'', since all other cases lead to a contradiction. But then > e'' and the only uncertain number w.r.t. k is r'.

case (b):

Both r and r' are 1 apart and are on even positions. In this case, we have r < e<= o < r' < e', but this is a contradiction, since r' is at even position and would have to appear between e and e'.

case (c):

r is on odd position and r' is adjacent. Then r < e<= r' < e' implies r'=e and so k > r'.

case (d):

r is on even position and r' is adjacent. Since e < k < e' and e<= r' < e', we must compare k with r'.

To conclude, in order to determine the exact position of k with respect to numbers in R, it must be compared with r'.

Back to the beginning of the page	Back to the CS838 class schedule

Complexity of Cole's EREW PRAM Merge Sort

Theorem

The algorithm EffMerge requires at most 4N comparisons to merge two sorted sequences of length N. Its parallel time is T(2N,N)=O(log N).

This implementation would be time-optimal, but not cost optimal, since the complexity of a merge operation of 2 N-number sequences is SU(2N)=O(N), whereas C(2N,N)=O(Nlog N). But we can scale easily this algorithm to get an optimal cost.

Theorem

The EffMerge takes parallel time O(log N) using N/log N processors.

T(2N,N/log N)=\alpha O(log N+(log N)/2+(log N)/4+...+1+...+1)

Theorem

The Cole's Merge Sort performs at most 2Nlog N comparisons to sort N numbers. It runs in parallel time O(log²N) using N/log N processors.

Back to the beginning of the page	Back to the CS838 class schedule