| Back to the beginning of the page | Back to the CS838 class schedule |
Why WH routing is an important switching technique?
The simplicity, low cost, and distance-insensitivity of wormhole switching are the main reasons behind its wide acceptance by manufacturers of commercial parallel machines. The following simple example demonstratessome arguments showing that 2-D wormhole torus can outperform WH hypercube of about the same cost. Assume we need to decide whether to use 2-D torus or hypercube for our parallel machine with wormhole routers. We can use various metrics for evaluating the cost of the network.- The cost of a network is proportional to the # of wires between routers.
- Assume full-duplex channels.
- p-vertex hypercube Qk, where k=log p, has k channels per router, whereas torus T(\sqrt{p},\sqrt{p}) has only 4 channels per router.
- Hence, Qk network with serial 1-wire channels will cost as T(\sqrt{p},\sqrt{p}) with k/4 wires per channel.
- The average distance in Qk is k/2 and the average distance in T(\sqrt{p},\sqrt{p}) is \sqrt{p}/2.
- Using Equation (7.2), the average base communication latency of a packet will be therefore
{log p/ 2}td+Mtmin Qk, whereas{\sqrt{p}/ 2}td+{4/ log p}Mtmin T(\sqrt{p},\sqrt{p}), since the torus parallel channels have log p/4 times higher bandwidth.
- The cost of a network is proportional to its bisection bandwidth.
- p-processor hypercube Qk has bisection width p/2, whereas p-processor torus T(\sqrt{p},\sqrt{p}) has bisection width 2\sqrt{p}.
- So, by a similar argument, Qk with serial 1-wire channels has the same bisection bandwidth as T(\sqrt{p},\sqrt{p}) with \sqrt{p}/4 wires per channel.
- The average base communication latency of a packet will be again
{log p/ 2}td+Mtmin Qk, but{\sqrt{p}/ 2}td+{4/ \sqrt{p}}Mtmin T(\sqrt{p},\sqrt{p}).
| Back to the beginning of the page | Back to the CS838 class schedule |
Virtual WH channels
- A physical WH channel may support several virtual channels multiplexed across the physical channel.
- Each unidirectional virtual channel is realized by an independently managed pair of (flit) buffers.
- Packets can share the physical channel on a flit-by-flit basis.
- The physical channel protocol must be able to distinguish between the virtual channels.
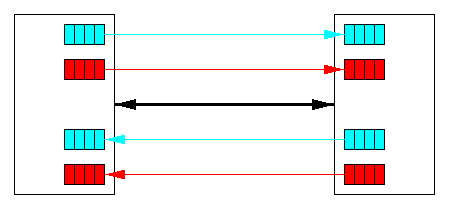
CAPTION: A physical channel divided into two (red and blue) virtual channels
Virtual channels were originally introduced to solve the deadlock avoidance problem, but they can be also used to improve network latency and throughput. Figure illustrates two model situations: Assume P0 arrived earlier and acquired the channel between the two routers first. In absence of virtual channels, packet P1 arriving later would be blocked until the transmission of P0 has been completed. Assume now that physical channels implement two virtual channels. Upon arrival of P1, the physical channel is multiplexed between them on a flit-by-flit bases and both packets proceed with half speed.
- Assume that P0 is a full-length packet whereas P1 is only a small control packet of size of few flits. Then this scheme allows P1 pass through both routers while P0 is slowed down for a short time corresponding to the transmission of few packets.
- Assume that P0 is temporarily blocked downstream from the current router. Then P1 can proceed at the full speed of the physical channel.
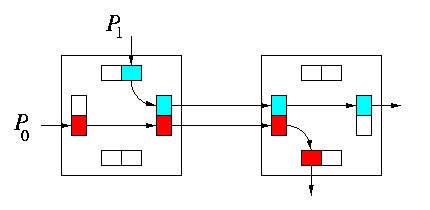
CAPTION: Increased throughput due to virtual channels
| Back to the beginning of the page | Back to the CS838 class schedule |
Undeliverable packets
Undeliverable packet situations
In every network, the number of resources is finite and the contention problem is the more severe, the more the network is loaded. The resources for which packets compete are- buffers in SF and VCT switching,
- channels in circuit and WH switching.
- a node cannot send a packet to itself,
- a packet that reached its destination is always consumed and ejected in finite time by this node,
- routing is distributed and deterministic,
- physical channels are bidirectional full-duplex and can be divided into virtual channels,
- routing and arbitration unit in router can only process one packet header at a time,
- if incoming packets content for this unit, it is allocated in a round robin way,
- if a packet acquired the routing and arbitration unit, but it cannot be routed since the required output channels are busy, it waits in the corresponding input buffer until its next round,
- virtual channels are assigned the physical channel cyclically only if they are ready to route a flit (demand-slotted round robin),
- once a buffer accepts the first flit of a packet, it must accept the remaining flits of the same packet before accepting any flits from another packet,
- Livelock:
- a packet is denied routing to its destination forever even though it is never blocked permanently. It may be traveling around its destination node, never reaching it because the channels it requires are always occupied by other packets. This can occur if nongreedy adaptive routing is allowed (packets are misrouted, but are not able to get closer to the destination).
- Starvation:
- a node with a packet is never allowed to inject it into the network (e.g., the traffic within the network is getting higher priority, which makes sometimes sense if the network is heavily loaded). Or a packet, already in the network, is permanently stopped if traffic is intense and the resources requested by it are always granted to other packets also requesting them.
- Deadlock:
- packets are allowed to hold some resources while requesting others, so that the dependency chain forms a cycle. Then all these packets must wait forever.
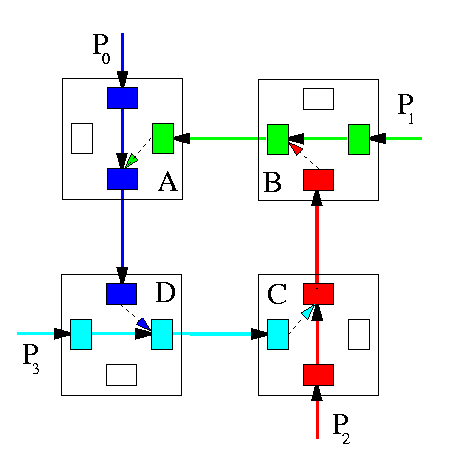
CAPTION: A deadlock situation in a wormhole network.
These abnormal situations may be related. For instance, a deadlock can permanently block exactly those resources that misrouted packets need to get out of a livelock. The probability of occurrence of situations preventing packets to be delivered increases with network traffic and decreases with the amount of buffer space. That is why WH is more deadlock-prone than VCT if the routing algorithm is not deadlock-free.
Handling undeliverable packets
- Starvation handling:
- Starvation can be solved easily if a correct and fair resource allocation scheme is used, such a simple demand-slotted round-robin scheme. If some packets must have higher priority than the others, then some part of the bandwidth must be reserved and guaranteed for lower-priority packets (virtual channels, extra buffers etc). In WH networks, this can be easily implemented.
- Livelock handling:
- The simplest way is to use greedy routing. In WH networks, it increases throughput since the worms have minimal possible length. If nongreedy routing is used, then the number of misrouting operation must be bounded.
- Deadlock handling:
- Deadlocks are the most difficult problem to solve among these three. It can be handled in three ways:
- deadlock prevention:
- resources are granted to packets in such a way that a request can never lead to a deadlock. This is done in circuit switching: the resources are granted before the transmission starts. It is very conservative approach and may lead to very low resource utilization.
- deadlock avoidance:
- resources are requested as a packet advances through the network so that the resulting global state is deadlock-free. This is less conservative, resources are requested only when they are really needed. A common technique is to establish an ordering between resources and granting them to each packet in descending order, which provides a deadlock-free routing algorithm, if such exists, for given topology. This is the case of dimension-order routing in meshes and binary hypercubes and it is discussed bellow.
- deadlock recovery:
- Deadlock is allowed, resources are granted to packets without any check, and if a deadlock is detected, some resources are deallocated and granted to other packets. This usually implies aborting some packet transmissions. This can be used only if deadlocks are rare and the results of aborts can be tolerated.
| Back to the beginning of the page | Back to the CS838 class schedule |
Deadlock avoidance theory
Definition
Consider a network G modeled by a directed graph where the bidirectional channels are implemented by pairs of antiparallel unidirectional channels. Let C be the set of these channels of G and V be the set of nodes (routers) of G. The routing function R in G is a function C× V-> C, which for each current input channel cin C and destination node w returns the output channel R(c,w).
Definition
Given a directed graph G and routing algorithm R, then the channel dependency graph for G and R, CDG(G,R), is a digraph D such that V(D)=E(G) and E(D) is the set of all pairs of adjacent channels used by routing algorithm R. Hence, ( ci,cj)in E(D) if and only if routing R can forward a packet from channel ci to channel cj for some communication request in G, i.e. if \exists destination node win V(G) such that R(ci,w)=cj.Figure illustrates the simplest possible case, 1-D torus.
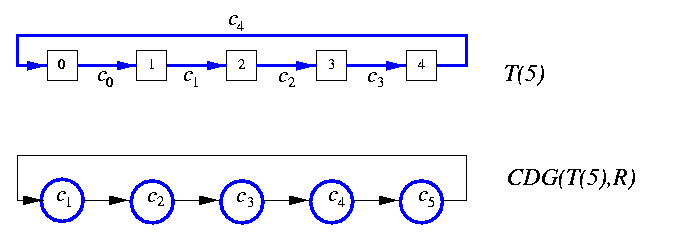
CAPTION: Torus T(5) and its channel dependence graph D
The deadlock avoidance theory stands on the following result.
Theorem
A deterministic routing algorithm R is deadlock-free in G if and only if CDG(G,R) is acyclic.Proof
(\Leftarrow) Suppose D=CDG(G,R) has a cycle S. It follows from our assumptions that D has no loops. Hence S must be of length l(S)>= 2. If S consists of two channels c1 and c2, then a pair of requests R(c1,w1)=c2 and R(c2,w2)=c1, where w1 and w2 are in distance at least 2 ahead from the packets, will deadlock. If l(S)>= 3, then a deadlock configuration is even easier to construct, just by submitting l(S) packets simultaneously, each injected in one node of S and destined to the node in G in distance two ahead following the channels in S.
Corollary
Dimension-order routing is deadlock-free in full-duplex meshes and binary hypercubes.Dimension-order routing in meshes can construct always a shortest path by checking dimension offsets in the current router address and destination address in decreasing order, so the CDG cannot contain cycles. Assume that the four routers in Figure form a 2× 2 submesh of a larger 2-D mesh. Then XY routing would lead to the situation on Figure , which clearly shows that deadlock cannot arise.
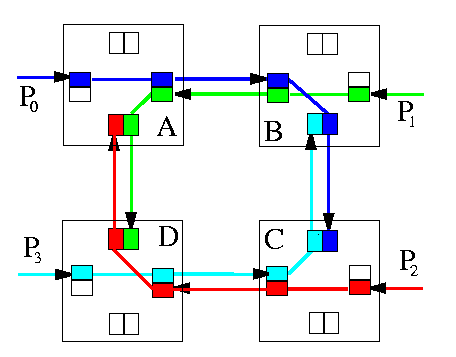
CAPTION: XY routing in 2-D mesh is deadlock-free
On the other hand, dimension-order routing is not deadlock-free in tori. Figure gives the simplest example. For example, each tuple of z packets P0,...,Pz-1, where Pi's source node is i and destination node is i+z2, leads to a deadlock. Every 1-D cycle has a cyclic CDG.
Generally,
Lemma
In k-ary n-dimensional tori, for k>= 5, there exists no deadlock-free greedy routing algorithm. However, using two virtual channels per physical one, there exists a deadlock-free nongreedy routing algorithm for tori.In general, if CDG(G,R) is cyclic, the following method allows to design a nongreedy deterministic deadlock-free routing algorithm for any G:
- Construct D=CDG(G,R).
- Try to break all cycles in D. Assume that D can be reduced to a directed acyclic graph (DAG) D' so that G remains strongly connected using routing function reduced to remaining channels. Then we have a routing function R' constrained to those channel dependencies that correspond to arcs in D' and since D' is acyclic, R' is deadlock-free.
- If the reduction cannot be done without making G strongly disconnected, then add arcs to D that correspond to splitting each channel of G into a group of q virtual channels (q>= 2). The additional edges provided by virtual channels make it possible to reduce D to strongly connected DAG while keeping G strongly connected. This reduction is based on lexicographic labeling of channels.
A solution for tori
We assume distributed routing and will describe the routing function implemented in every router. Consider a general torus T(z1,...,zn), node coordinates start at 0, and each node is labeled with n-letter strings with mixed radixes zi.- Node u has n output physical channels labeled with (n+1)-letter strings iu, i=0,...,n-1, denoted by ciu (see Figure ).
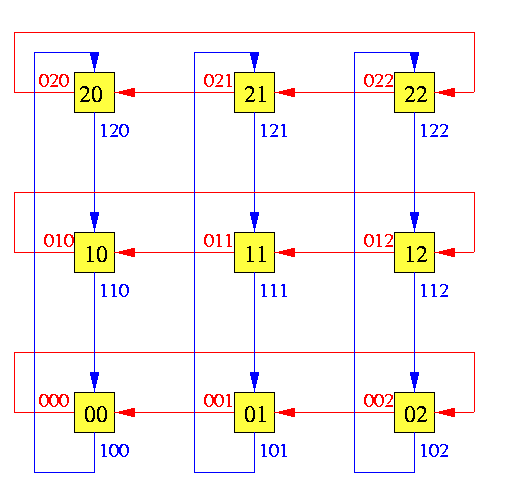
CAPTION: Channel labeling in 2-D torus
- Each physical channel ciu is divided into two virtual channels: upper ci1u and lower ci0u.
- Informally a deadlock free routing function is defined as follows:
- route in order of descending node addresses:
- find the nonzero offset in the most significant position (from left to right) by subtracting current address from the destination
- make a step towards its nullifying by sending the packet along that dimension in descending order so that
- use the upper virtual channel if the corresponding offset is > 0
- use the lower virtual channel if the corresponding offset is < 0
- route in order of descending node addresses:
- The formal definition of the new routing function is as follows:
R'(cdru,w)=
cd1v if vd < wd
cd0v if vd > wd
ci1v if for all k > i; vk=wk and vi < wi
ci0v if for all k > i; vk=wk and vi > wi
Lemma
The routing function R correctly routes packets from any node to any other node in T(z1,...,zn).Proof
By induction over n.
c1v,...,c10,c0(z-1),...,c0(w+1),which will deliver it to w. If v > w, then the packet will follow path of channels
c0v,...,c0(w+1),which will deliver it to w as well. The induction step is by decomposition of n-dimensional tori to a cartesian product of a cycle and (n-1) -dimensional subtori. As an example, consider again the simplest case of T(5) on Figure . Using two virtual channels is fairly easy here. Whenever is a packet destined to a node which is in the descending segment the lower virtual channels are used. If the destination is in the upper segment with respect to the source, then the packet starts moving left using upper channels until it reaches node z-1 when it switches to lower channels and keeps using them until it reaches the destination. Note that channels c00 and c1(z-1) are never used.
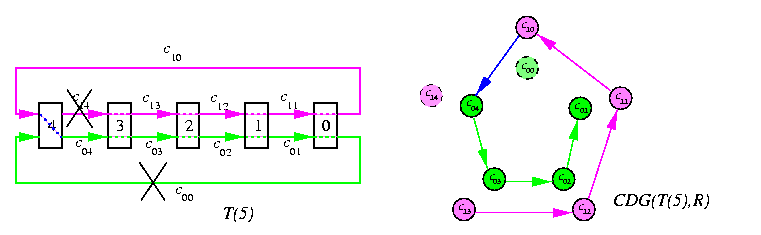
CAPTION: Deadlock-free routing in T(5) using two virtual channels and the corresponding acyclic CDG
The following example shows a typical permutation of packets which would establish a deadlock if there were no virtual channels. It is cyclic rotation by two positions to the right (it works for any number of positions). Packets form a chain ending with an unblocked buffer, so even if they start at the same time, each of them will eventually make progress.
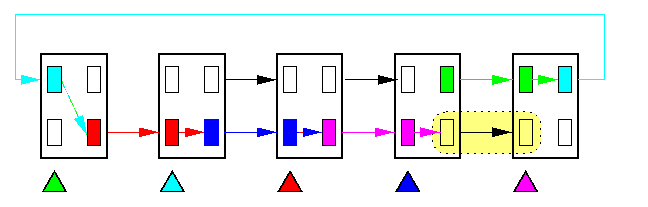
CAPTION: Routing of a cyclic-2-shift on T(5)
| Back to the beginning of the page | Back to the CS838 class schedule |