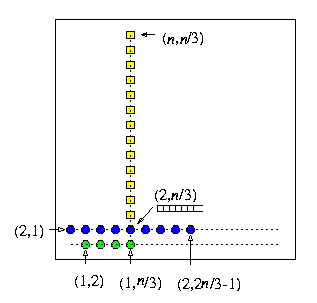Permutation routing in mesh-based networks

Section#9: Permutation routing in mesh-based networks
(CS838: Topics in parallel computing, CS1221, Tue, Feb 23, 1999, 8:00-9:15 a.m.)

The contents

Farthest-first routing in 1-D meshes
XY greedy permutation routing in 2-D mesh
Approaches to minimize the buffer requirements for permutation routing
Average-case behavior of greedy permutation routing
Randomized permutation routing
Sorting-based permutation routing
Off-line permutation routing

Permutation routing on 2D-meshes are relatively simple and straightforward and still many general observations and useful conclusions can be made on them. We will consider both complete and partial permutation routings: each node can a source and/or destination of at most one packet. We will investigate store-and-forward meshes only here, partially due to lack of space, partially due to the fact, that the permutation routing results known for wormhole meshes are less understood and more complicated.

Back to the beginning of the page

Back to the CS838 class schedule

Farthest-first routing in 1-D meshes

On 1-D mesh, permutations are fairly easy. The following result applies to a more general case, when every node is a destination of at most one packet, whereas one node can initially hold more that one packet.

Lemma

Consider a linear array M(n) of n nodes with full-duplex all-port links and SF switching, and with O(n)-packet buffers. Assume a one-to-one routing problem where each node is a source of any number of packets, but globally, there exists at most one packet destined for each node. Then farthest-first greedy routing strategy needs at most n-1 steps (hops) to deliver all packets.

Proof
(By induction on the length of paths packets have to travel.)

Since the channels are full-duplex, packets moving in opposite directions can never interfere so that each node (except the corner ones) can inject two packets and receive two packets at each step. So we will examine only packets moving in the same direction, say rightward.
Routers implement the farthest-first strategy to resolve possible channel contention: if they have more packets to be sent in the same direction, the priority is given to the packet that has the longest path ahead.

CAPTION: The farthest-first greedy routing on 1-D mesh
The inductive proof is based on the fact that packets destined for the rightmost nodes in the array keep moving once they start.
- Fix integer i, 1<= i<= n-1, define i-priority packets as packets destined for the rightmost i nodes. Let Z_i denote the zone of the last i rightmost nodes in M(n).
- Let k, k<= i, be the number of i-priority packets.
- Let P_j, 1<= j<= k, be the j-th rightmost i-priority packet.
- The strategy farthest-first can never delay an i-priority packet due to a non-priority packet. (An i-priority packet has always father to go than non-i-priority one.)
- If a node has more i-priority packets, the ordering follows the farthest-first rule.
- Packet P₁ starts moving in the first step (if n=6 and i=3, then k=3 and P₁ is packet # 4 in Figure ).
  - Once P₁ starts, it cannot be delayed by other packets.
  - After the first step, P₁ cannot meet, and therefore delay, in other nodes any other i-priority packet. (P₁ was the rightmost i-priority packet and it is always ahead of all other i-priority packets until it reaches its destination).
  - P₁ reaches Z_i in at most n-i steps.
- Packet P₂ may be delayed during the first step by P₁, so it will start moving in the second step at latest. (P₂ is packet # 6 in Figure , it moved in the first step and became the second rightmost 3-priority packet). Similarly to P₁,
  - once P₂ starts, it keeps moving until it reaches its destination,
  - neither P₁ and P₂ can delay any of the other i-priority packets after step 2,
  - P₂ will reach Z_i in at most n-i+1 steps.
- Inductively, the last i-priority packet P_k cannot be delayed after step k-1, because all other i-priority packets started already to move rightward and none of them can be stopped after step k-2 unless they reach their destinations.
- In the worst case, k=i and P_i is still in the leftmost node in step i-1 and it has n-i edges to traverse to get to its destination, the i-th rightmost node. Therefore, at most (i-1)+(n-i)=n-1 steps are needed for P_i to reach its destination.
Since the argument holds for any i, 1<= i<= n-1, the lemma is proved.

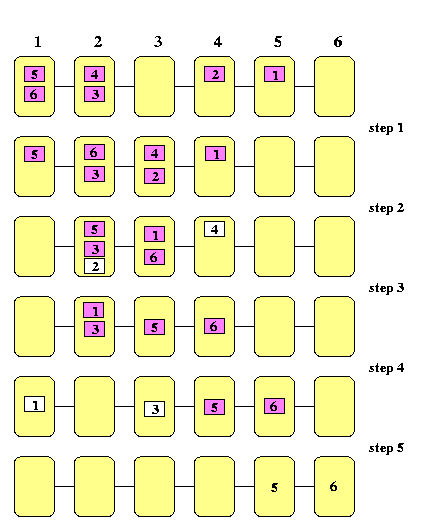
Note that if every node in M(n) has initially at most one packet to send, then all packets start moving in the first step and the routing is contention-free as shown on Figure .

CAPTION: A simple permutation on a 1-D mesh

Back to the beginning of the page Back to the CS838 class schedule

XY greedy permutation routing in 2-D mesh

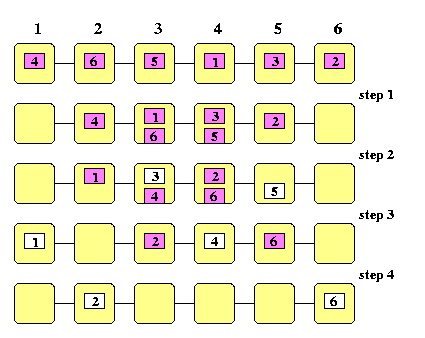
Lemma has one important implication. If we take any N-node 2-D mesh, we can perform any permutation of N packets between nodes in the optimum number of steps, but to achieve that, we will need to store O(N) packets in one router at one time in the worst case. This raises a general question about the tradeoffs between the time and memory requirements of permutation routing algorithms. We will assume here that every k-port router has k input and k output buffers for one packet. Some algorithms, however, require larger buffer space to achieve time optimality. Some of packets received in one step must wait in routers for later steps due to contention on the same output channel. At the same time, the next packets waiting on input channels must proceed, if the output channels they require are free, so that the input buffers must be released by the waiting packets and we need auxiliary buffers. In general, we will assume that each router has auxiliary buffers for \beta packets in addition to the standard ones. Our desire of course is to minimize \beta. A permutation is memory-optimal if \beta=O(1). Hence, the first result is not memory-optimal.

Lemma

Consider store-and-forward all-port mesh M(n,n), n>= 2, with full-duplex channels and any permutation routing problem on M(n,n). Using greedy XY routing, at most 2n-2 steps is needed to complete the permutation (which is optimal, since the diameter of M(n,n) is 2n-2), but \beta=max(2,2n/3-1).

Proof

In the first step, all packets which are not in their destination columns, start moving horizontally. Since each node has initially only one packet to send and channels are full-duplex, packets keep moving horizontally without contention, until they reach their destination columns. Hence, each packet will reach its correct column in at most n-1 steps.
Within columns, the farthest-first routing used in Lemma applies to packets, gathered in buffers of column nodes. By this lemma, this will take again at most n-1 steps.

CAPTION: An example of a XY-routing permutation on a SF full-duplex mesh M(3,3)
The buffers in each router must be for at least max(2,2n/3-1) packets.
- (Constructive proof.) Assume for simplicity that n is divisible by 3, that columns are numbered from left to right and rows are numbered bottom up, starting from 1.
- The worst buffer-size scenario is the following (see Figure ): Let u be the node (2,n/3).
  - Assume that packets in nodes (2,1)...(2,2n/3-1) (blue circles in Figure ) and in nodes (1,2)...(1,n/3) (green circles) are all destined for nodes (3,n/3)...(n,n/3) (yellow squares).
  - The number of these packets as well as destination nodes is n-2.
  - In each step during the first n/3-1 steps, node u can send upward only one packet, but has to receive three packets.
  - Thus, u has to receive the total of n-2 packets while only n/3-1 packets will leave it in the meantime.
  - Hence, after n/3-1 steps, the auxiliary buffers in u have to store n-2-(n/3-1)= 2n/3-1 packets.
- Clearly, another lower bound on \beta is 2, since in the worst case, each node can receive three packets from three directions, heading to the same part of its column. Then only one of them can proceed to the output channel, whereas the other two must be stored in auxiliary buffers to release the input buffers.

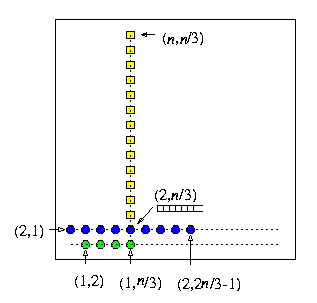
CAPTION: The worst buffer-size scenario for XY greedy permutation routing in M(n,n).
A similar argument can be used for higher-dimensional meshes.

Corollary

Consider store-and-forward all-port k-ary n-dimensional mesh M=M(k,...,k), k>= 2, n>= 3, with full-duplex channels and any permutation routing problem on M. Using greedy dimension-order routing, at most n(k-1) steps is needed to complete the permutation (which is optimal, since it equals to the diameter), but nodes need buffers for max(2n-2,k-2-(k-3)/(2n-1)) packets.

Back to the beginning of the page

Back to the CS838 class schedule

Approaches to minimize the buffer requirements for permutation routing

The result of Lemma implies that the size of buffers in a 2-D mesh depends linearly (!) on the square root of the network size. The question we should ask now is whether there are routing algorithms for permutation problems on meshes that are time-optimal and memory-optimal. Unfortunately, this problem is rather hard. In general, there exist three common approaches:

randomization
sorting-based permutation routing
off-line permutation routing

Back to the beginning of the page

Back to the CS838 class schedule

Average-case behavior of greedy permutation routing

For random permutations, the worst-case scenario in previous lemma is very unlikely. In a random permutation, each processor has one packet that is destined for a randomly chosen destination. For given source, each destination is equally likely to be chosen and two sources choose their destinations independently. One node can become a destination of more than one packet, but it is unlikely that this number will be too large. In \cite{ftlbook}, the following result is proved.

Lemma

When the XY greedy routing is used for a random permutation problem on M(n,n), then

\beta<= 4 with probability 1-O(log⁴n/n),
any packet will be delayed z steps with probability O(e^-z/6),
any packet with destination in distance d will reach its destination in d+O(log n) steps with probability 1-O( 1/n² ).

Back to the beginning of the page

Back to the CS838 class schedule

Randomized permutation routing

The previous results apply only to random permutations. In practice, however, many useful permutations are not very random, they very often tend to the worst-case behavior rather than random. For example in 2-D meshes, there are many permutations in which many packets in one row want to go to the same column, and then XY routing needs large buffers. A practical example is transposition of a matrix with block-checkerboard mapping (see Chapter ). The simplest approach to reducing the maximum buffer size is to convert the worst-case permutation routing problem into two random permutation problems (it can applied to any network, not only to 2D-meshes): Given a permutation \pi on the set of processors 1,...,p, generate for each pair (i,\pi(i)) a random intermediate node g(i) and then send packet i first to g(i) and from g(i) to \pi(i), using the greedy deterministic routing in both phases. Insertion of random intermediate nodes will increase the time, but the packets will very likely be scattered across the network uniformly. The uniformity of distribution of the traffic depends on the choices of the random intermediate destinations and not on the routing problem itself. Thus, it works on any problem with high probability. The best possible known results for meshes is the following.

Lemma

Any permutation routing on M(n,n) can be solved using this randomization approach in 2n+O(log n) steps using \beta=O(1) buffers with high probability.

The proof of this result is quite difficult, here we sketch a simpler strategy which still provides a good performance.

Lemma

Any permutation routing on M(n,n) can be solved using randomization in 2n+o(n) steps using \beta=O(log n) buffers with probability at least 1-O(1/n²).

The algorithm achieving this behavior works as follows:

Phase 1a:: each column is partitioned into log n intervals of size n/log n,
Phase 1b:: each packet is routed to a randomly selected destination within its interval,
Phase 2:: each packet is routed within its current row to its correct column,
Phase 3:: each packet is routed within its correct column to its correct row.

If there is a contention on channels, the routers use again the farthest-first strategy.

Back to the beginning of the page

Back to the CS838 class schedule

Sorting-based permutation routing

Since randomized approaches can fail in some cases, it is more satisfactory to have good deterministic solutions. One useful approach is to sort the packets first. It can again be applied to any network, on 2D-meshes it works as follows.

Lemma

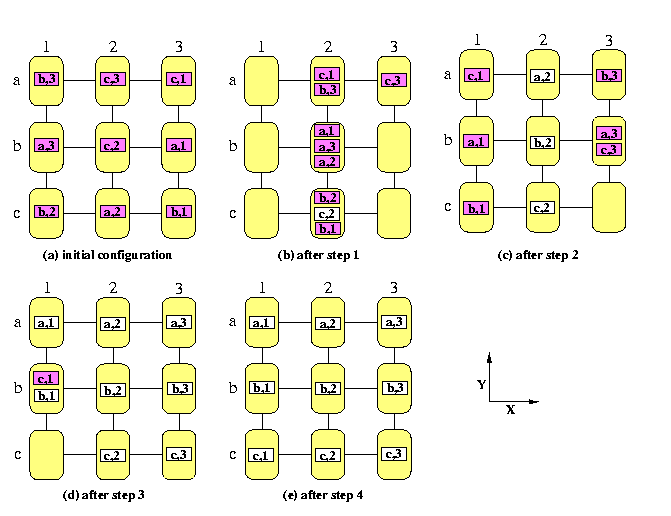
Permutation routing on all-port store-and-forward M(n,n) with full-duplex channels can be performed in O(s(n)+3n) steps with \beta=0, where s(n) is the parallel time complexity of sorting n² numbers on M(n,n) into snake-like order.

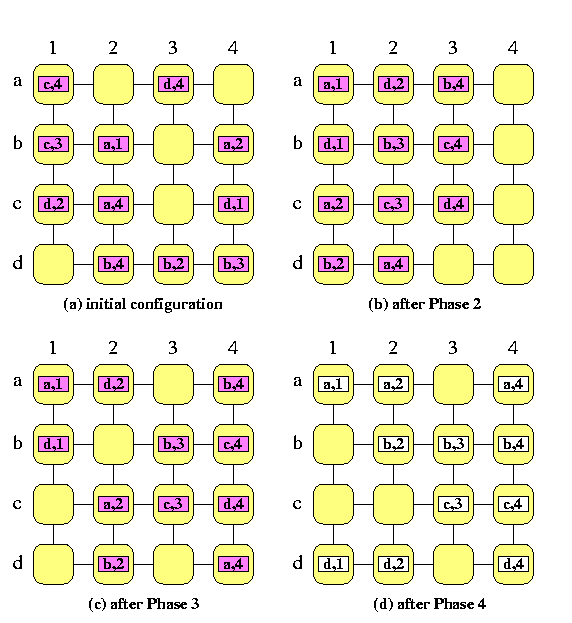
CAPTION: Sorting based permutation routing on a SF full-duplex mesh M(4,4)
Proof
Sorting algorithms for meshes will be described in Section #16. Here we will just assume that

there is a sorting algorithm for snake-like ordering of n² numbers on all-port store-and-forward full-duplex M(n,n) with \beta=0 whose parallel time complexity is s(n)=3n+o(n).

Then the permutation routing needs T(n)=6n+o(n) steps, which is optimal up to the multiplicative constant. The routing algorithm proceeds in 4 phases.

Phase 1:: Sort packets into global column-major snake-like ordering according to destination column addresses. We get a vertical global snake, starting with packets destined to the first column, followed by packets destined to the second, third, and so on, columns. Each group of packets with the same destination column address has size at most n.
Phase 2:: Reverse every second column to get a column-major global ordering. It is a trivial conflict-free permutation completed in n-1 steps. Since each group of packets with the same destination column address has size at most n, it follows that in each row, there is at most one packet destined for any given column
Phase 3:: In all rows in parallel, perform permutation routing to correct columns. Since no two packets go to the same column, it is again a trivial n-1 step routing problem. Since the packets are already in correct columns, in each column, there is at most one packet destined for any given row.
Phase 4:: In all columns in parallel, perform permutation routing to correct rows. This takes again n-1 steps.

It follows from the description of the algorithm that in all steps, we need no auxiliary buffers.

Back to the beginning of the page

Back to the CS838 class schedule

Off-line permutation routing

The sorting-based algorithm was an on-line solution. They must be used if the permutation to be routed is not known in advance. Each node knows only about its own packet and all nodes together rearrange the packets into a suitable ordering. The information about the permutation is distributed among nodes. In many applications, the same permutation is routed repeatedly and it is known in advance. A typical example is a simulation of one network or parallel computer on another one. We will see such examples in Section #10. Then we have centralized global information about the whole permutation and we can precompute off-line the best possible, i.e., time- and memory-optimal, routing.

Lemma

There is an off-line algorithm which for any permutation on M(n,n) precomputes (3n-3)-step routing with \beta=0.

Proof
The algorithm has also 4 phases, the last two phases are the same as in the previous algorithm.

Phase 1:: precompute for each column a permutation such that after performing these permutations, there is at most one packet in each row destined for any given column.
Phase 2:: Perform these permutations in all columns in parallel.
Phase 3:: In all rows in parallel, perform permutation routing to correct columns.
Phase 4:: In all columns in parallel, perform permutation routing to correct rows.

We will show constructively that the permutations of columns we need to precompute always exist. The proof is based on a basic result of combinatorics, on Hall's matching theorem.

bipartite graph G:: V(G)=X\cup Y, E(G)\subset X× Y (every edge in E(G) joins X with Y). Without loss of generality, assume |X|<=|Y|.
matching in G:: = E₁\subset E(G) such that no vertex of G is incident with at most one edge in E₁.
perfect (complete) matching from X to Y:: = matching in G such that every vertex in X is incident with exactly one edge of the matching
marriage (dance party) problem:: If the vertices in X and Y represent boys and girls, respectively, and an edge joins two persons with mutually amicable feelings and therefore willing to dance together, then the problem is to form dancing pairs so that every boy gets a girl towards which he has amicable feelings.

Theorem

(Hall's Matching Theorem) A necessary and sufficient condition for there to be a perfect matching from X to Y in G is that
|\Gamma(A)|>=|A| for any A\subseteq X,
where \Gamma(A) is the set of neighbors of vertices in A, i.e., \Gamma(A)={yin Y; ( x,y)in E(G), xin A}.

For our purposes, we only need a special instance of this theorem.

Corollary

Any regular bipartite graph has a perfect matching.

The way how to apply this result to our permutation problem is the following. It works for any 2-D mesh.

For a given permutation \pi on M(m,n), construct so called routing bipartite graph G_\pi
- with vertex sets X={s₁,...,s_n} and Y={d₁,...,d_n}, where s_j and d_j represent the j-th source and destination column of M(m,n), respectively
- there is an edge between s_j₁ and d_j₂ iff column j₁ of M(m,n) contains a packet with destination column j₂.
- if \pi is a complete permutation, then G_\pi is an m-regular bipartite graph.
- if \pi is a partial permutation, extend it to a complete permutation by inserting dummy packets (= edges in G_\pi).
use the Hall's theorem to decompose the edge set of G_\pi into m edge-disjoint perfect matchings, or equivalently, construct an m-coloring of G_\pi.

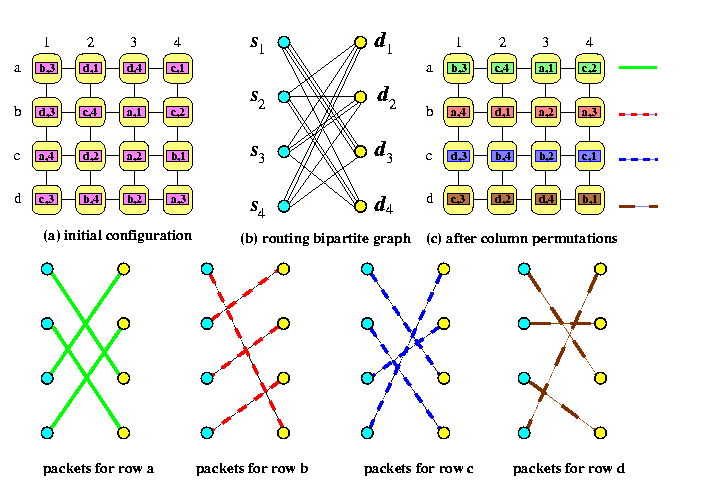
CAPTION: Precomputation of column permutations for off-line permutation routing on M(4,4) using a 4-coloring of the routing graph
How does this m-coloring of G_\pi relate to our problem? The trick of this method is that

an n-edge perfect matching of color i \approx n packets moved to row i in the column permutations

Since each vertex s_jin X has all m incident edges colored with m different colors, each packet in column j will be sent to another row, so the rearrangements of columns will certainly be permutations.
Since all n edges in the perfect matching are incident to n distinct vertices in Y, no row of M(m,n) after the column permutations can contain two packets with the same destination column.

Figure shows a solution on M(4,4). It remains to sketch how to construct an m-coloring of G_\pi. We need only explain how to construct one perfect matching, since when we have one perfect matching constructed, we remove its edges from G_\pi which results into an (m-1)-regular bipartite graph and we construct another perfect matching until we are left with a 1-regular bipartite graph whose edges form a perfect matching by definition.

Construction of one perfect matching in G_\pi

Consider an m-regular bipartite routing graph, m>= 2, as defined above.
A perfect matching is constructed iteratively by adding edges, i.e., inductively over the size of the matching. Assume we have a partial matching M in G_\pi with k edges, 1<= k < n. Then we can always construct a matching M' with k+1 edges (the edges of M are not necessarily included into M', but we will certainly use them for constructing M').
Let us call the edges of M red and all the other edges of G_\pi will be called blue.
Let s₀in X be a vertex not incident with any red edge. Then we prove constructively that \it there exists a simple path P of odd length, starting in s₀ with a blue edge, using red and blue edges alternatively, and terminating with a blue edge in a vertex in Y that is not incident with any red edge. If we find such a path P, we are done, because we obtain a matching with m+1 edges by deleting the red edges of P from M and by adding all blue edges of P to M (hence, we switch the colors of edges in P), which increases the number of edges in the matching by one.
Since s₀ is not incident with a red edge and G_\pi is m-regular, there exists d₀in Y, adjacent to s₀ by a blue edge.
If d₀ is not incident with a red edge, the edge ( s₀,d₀) is the required path of length 1.
If d₀ is incident with a red edge, let s₁ be the other end of the red edge.
By induction, we define vertices s₀,s₁,s₂,... and d₀,d₁,d₂,... as follows.
- Assume we have defined vertices s₀,...,s_k and d₀,...,d_k-1 for k>= 1.
- Since G_\pi is regular, there are at least k+1 distinct vertices in Y that are adjacent to vertices s₀,...,s_k.
- Hence, there exists a vertex d_kin Y distinct from d₀,...,d_k-1 and adjacent to at least one vertex among s₀,...,s_k.
- If d_k is not incident with a red edge, we stop.
- Otherwise, let s_k+1 be the other end of the red edge.
When this procedure terminates in vertex d_k for some k>= 1, we construct the path by starting in d_k. Recall that each vertex in {s₁,...,s_k,d₀,...,d_k-1} is incident with a red edge, whereas s₀ and d_k are not. Hence, there is a blue edge from d_k to some s_i₁, 0<= i₁<= k. This is the first edge of the constructed path. But we know that there exists a red edge ( s_i₁,d_i₁-1) and that d_i₁-1 is joined by a blue edge to some s_i₂, i₂ < i₁. We add edges ( s_i₁,d_i₁-1) and ( d_i₁-1,s_i₂) to the path, until s₀ is reached.

Figure illustrates this idea on a simple example.

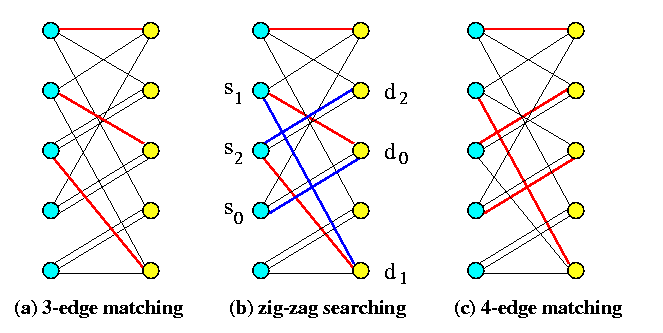
CAPTION: An example of one inductive step in building a (k+1)-edge matching from a k-edge one

Back to the beginning of the page Back to the CS838 class schedule

Section#9: Permutation routing in mesh-based networks(CS838: Topics in parallel computing, CS1221, Tue, Feb 23, 1999, 8:00-9:15 a.m.)

The contents

Farthest-first routing in 1-D meshes

XY greedy permutation routing in 2-D mesh

Approaches to minimize the buffer requirements for permutation routing

Average-case behavior of greedy permutation routing

Randomized permutation routing

Sorting-based permutation routing

Off-line permutation routing

Construction of one perfect matching in G\pi

Section#9: Permutation routing in mesh-based networks
(CS838: Topics in parallel computing, CS1221, Tue, Feb 23, 1999, 8:00-9:15 a.m.)

Construction of one perfect matching in G_\pi