Research Interests

Machine Learning and Computer Vision

• Revealing structure in Unsupervised data, Matrix Factorization, Multi-scale methods
• Theory and Design of Deep Networks, Regularizing Neural Networks
• Interpretability/Explainability of Nonlinear Models

Nonparametric Statistics

• Computationally Efficient Testing, Robust Resampling Methods

Applications

• Learning Models in Data Sciences, Deep Network Designs for Biomedical studies
• Multi-source Data Integration/Harmonization

Current and Past Projects

• Incremental Multi-resolution Matrix Factorization for modeling hierarchical block-structured data
  
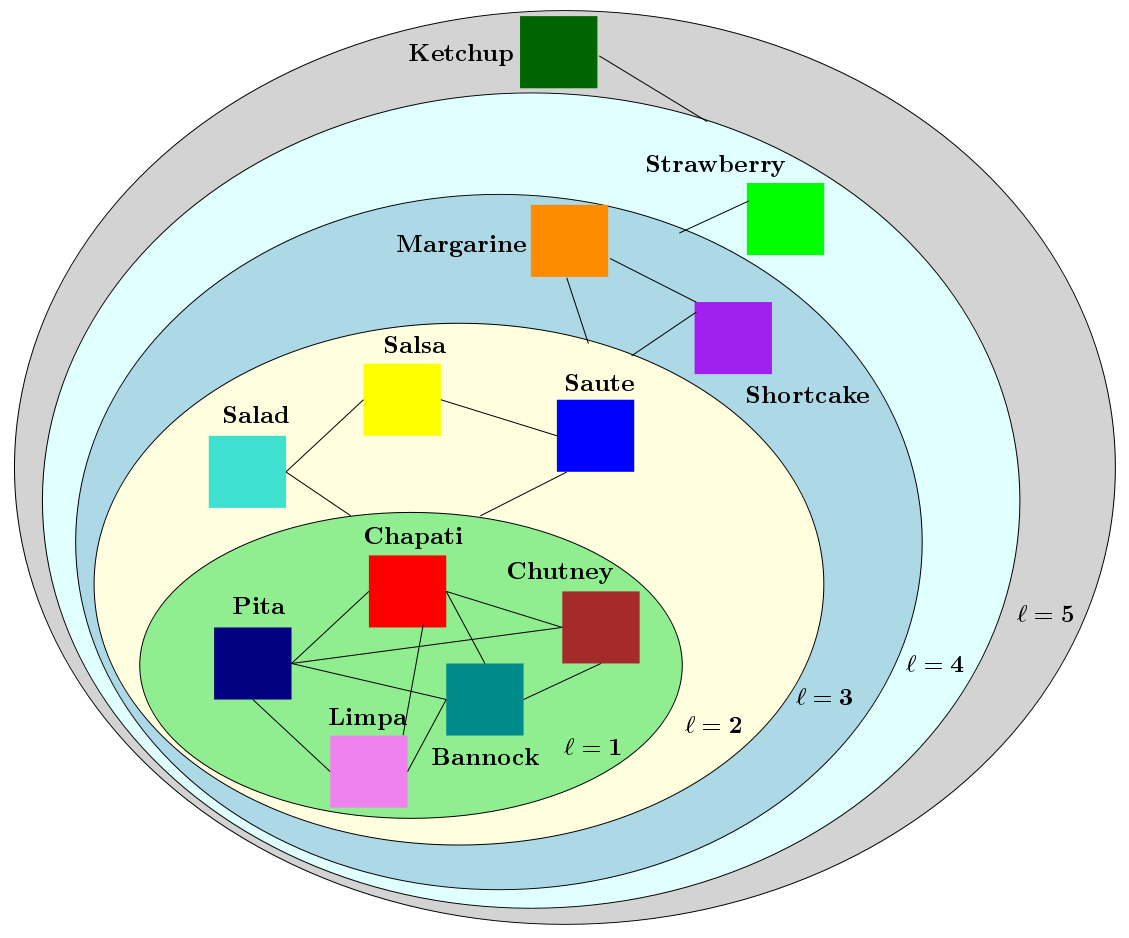
  Multiresolution analysis, e.g., Wavelets, and matrix factorization are foundational tools in computer vision. In [PDF], we study the interface between these two distinct topics and obtain techniques to uncover hierarchical block structure in symmetric matrices. Exploiting such ``structure'' directly or via implicit means often plays a critical role in the success of many vision problems. Our new algorithm, the {\it incremental multiresolution matrix factorization}, uncovers such structure one feature at a time, and hence scales well to large matrices. We describe how this multiscale analysis goes much farther than what a direct ``global'' factorization of the data can identify. We evaluate the efficacy of the resulting factorizations for relative leveraging within regression tasks using medical imaging data. We also use the factorization on representations learned by popular deep networks, providing evidence of their ability to infer semantic relationships even when they are not explicitly trained to do so. Our experimental results suggest how this algorithm can be used as an exploratory tool to improve the network architecture, and within numerous other settings in vision. Further description about the ideas and the MATLAB codes for the algorithm can be found here [IncMMF]
  
  
• Deductive Mode-finding for Outlier/Instance Selection
  
  Identifying associations between early decline in cognition to amyloid burden, is important in understanding preclinical Alzheimer’s disease (AD). Unsupervised clustering may have limited success in the preclinical stage when distinct subgroups are weak or not yet evident. The goal of this project is to propose a machine learning framework for identifying sub-groups within preclinical AD cohorts and provide evidence of potentially distinct cognitive temporal profiles. The proposed model’s null hypothesis assigns all samples to one initial cluster. Using likelihood ratio statistic, we select the participant with cognitive profile that deviates the most from the rest; and repeat the process recursively. This deductive procedure removes one subject at-a-time, eventually retaining a “core” group.
  
  
• Design choices in deep learning   [Design Choice Interface]
  
• Theory and convergence of deep learning
  
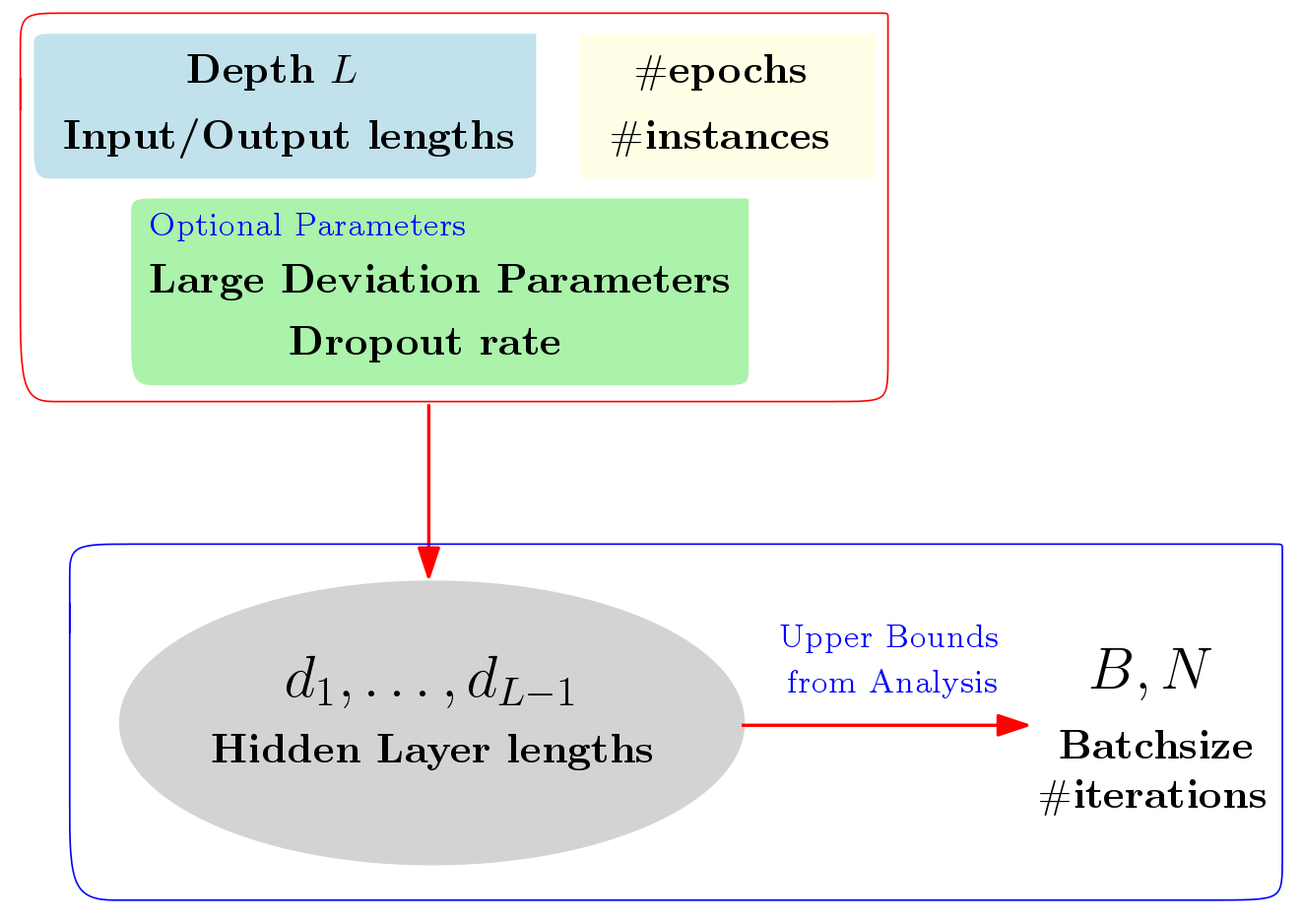
  We study mechanisms to characterize how the asymptotic convergence of backpropagation in deep architectures, in general, is related to the network structure, and how it may be influenced by other design choices including activation type, denoising and dropout rate. We seek to analyze whether network architecture and input data statistics may guide the choices of learning parameters and vice versa. Given the broad applicability of deep architectures, this issue is interesting both from theoretical and a practical standpoint. Using properties of general nonconvex objectives (with first-order information), in [PDF] and [PDF], we first build the association between structural, distributional and learnability aspects of the network vis-\`a-vis their interaction with parameter convergence rates. We identify a nice relationship between feature denoising and dropout, and construct families of networks that achieve the same level of convergence. We then derive a workflow that provides systematic guidance regarding the choice of network sizes and learning parameters often mediated4 by input statistics. Our technical results are corroborated by an extensive set of evaluations, presented in this paper as well as independent empirical observations reported by other groups. We also perform experiments showing the practical implications of our framework for choosing the best fully-connected design for a given problem.
  Based on the work from [PDF], we provide a web-interface that allows the users to input some resource constraints (e.g., like available number of instances, affordable input and output layer lengths etc.), and outputs the optimal (as predicted by our analysis) network structure for the given task. This web-interfance, both for the case where unsupervised data is available and the fully-supervised setting, can be accessed at [Design Choice Interface]
  
  
• Statistical Theory for Data Harmonization
  
• When is it valid to pool data from multiple sites in medical studies?
  
  Consider samples from two different data sources $\{\mathbf{x_s^i}\} \sim P_{\rm source}$ and $\{\mathbf{x_t^i}\} \sim P_{\rm target}$. We only observe their transformed versions $h(\mathbf{x_s^i})$ and $g(\mathbf{x_t^i})$, for some known function class $h(\cdot)$ and $g(\cdot)$. Our goal is to perform a statistical test checking if $P_{\rm source}$ = $P_{\rm target}$ while removing the distortions induced by the transformations. This problem is closely related to concepts underlying numerous domain adaptation algorithms, and in our case, is motivated by the need to combine clinical and imaging based biomarkers from multiple sites and/or batches, where this problem is fairly common and an impediment in the conduct of analyses with much larger sample sizes. In [PDF] we develop a framework that addresses this problem using ideas from hypothesis testing on the transformed measurements, where in the distortions need to be estimated {\it in tandem} with the testing. We derive a simple algorithm and study its convergence and consistency properties in detail, and we also provide lower-bound strategies based on recent work in continuous optimization. On a dataset of individuals at risk for neurological disease, we show that our results are competitive with alternative procedures that are twice as expensive and in some cases operationally infeasible to implement.
  
  
• Randomized deep networks for clinical trial enrichment   [Toolbox from NITRC]
  
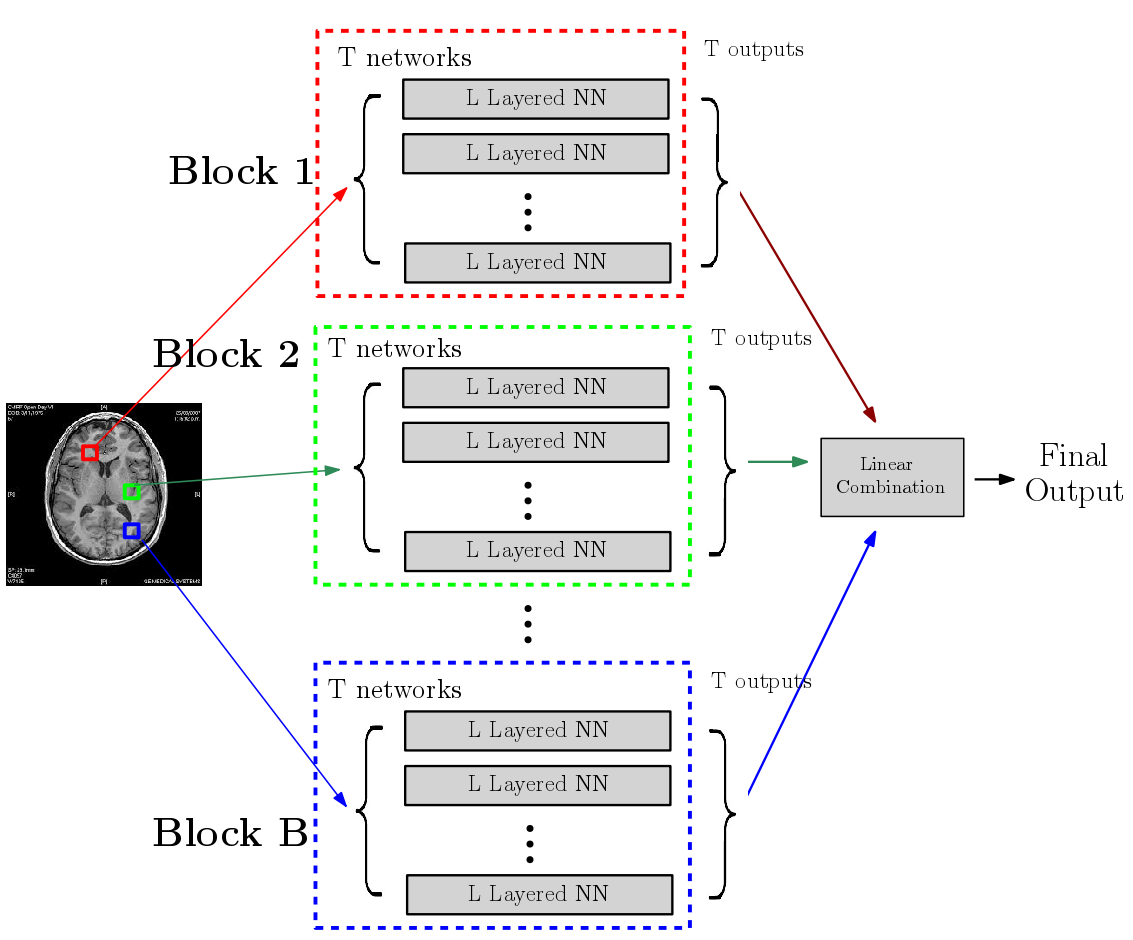
  There is growing body of research devoted to designing imaging-based biomarkers that identify Alzheimer’s disease (AD) in its prodromal stage using statistical machine learning methods. Recently several authors investigated how AD clinical trials can be made more efficient using predictive measures from such computational methods. For instance, identifying Mild Cognitive Impaired who are most likely to decline during a trial, and thus most likely to benefit from the treatment, will improve trial efficiency and power to detect treatment effects. To this end, using multi-modal, imaging-derived, inclusion criteria may be especially beneficial. In [PDF], [PDF], and Chapter 15 from [Elsevier Link], we explain why predictive measures given by ROI-based summaries or SVM type objectives may be less than ideal for use in the setting described above. We give a solution based on novel deep learning models referred to as a randomized neural networks. We show that our proposed models trained on multiple imaging modalities correspond to a minimum variance unbiased estimator of the decline and are ideal for clinical trial enrichment and design. The resulting predictions appear to more accurately correlate to the disease stages, and extensive evaluations on Alzheimer's Disease Neuroimaging Initiative (ADNI) indicate strong improvements in sample size estimates over existing strategies including those based on multi-kernel learning. From the modeling perspective, we evaluate several architectural choices including denoising autoencoders and dropout learning. Separately, our formulation empirically shows how deep architectures can be applied in the large d, small n regime -- the default situation in medical imaging and bioinformatics. This result is of independent interest.
  
  
• Budget constrained selection in linear models
  
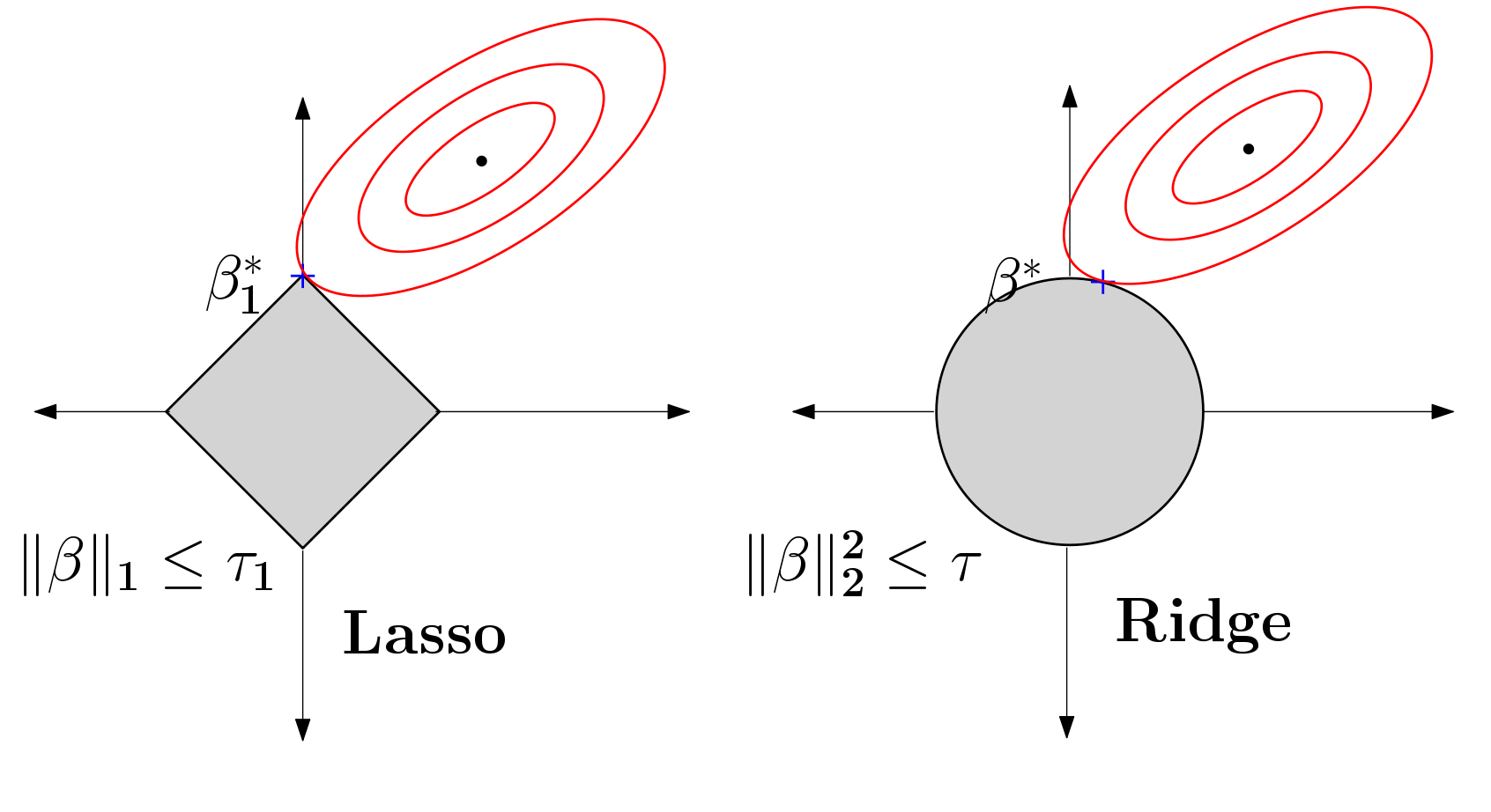
  Budget constrained optimal design of experiments is a well studied problem. Although the literature is very mature, not many strategies are available when these design problems appear in the context of sparse linear models commonly encountered in high dimensional machine learning. In [PDF], we study this budget constrained design where the underlying regression model involves a $\ell_1$-regularized linear function. We propose two novel strategies: the first is motivated geometrically whereas the second is algebraic in nature. We obtain tractable algorithms for this problem which also hold for a more general class of sparse linear models. We perform a detailed set of experiments, on benchmarks and a large neuroimaging study, showing that the proposed models are effective in practice. The latter experiment suggests that these ideas may play a small role in informing enrollment strategies for similar scientific studies in the future.
  
  
• Efficient (fast and accurate) Permutation Testing (Exploiting redundancy in non-parametric testing)   [RapidPT Tool]
  
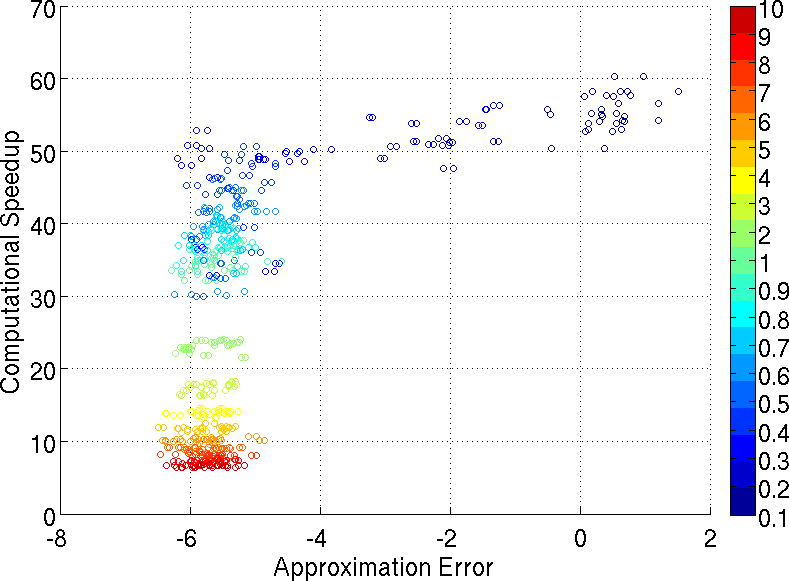
  Multiple hypothesis testing is a significant problem in nearly all neuroimaging studies. In order to correct for this phenomena, we require a reliable estimate of the Family-Wise Error Rate (FWER). The well known Bonferroni correction method, while simple to implement, is quite conservative, and can substantially under-power a study because it ignores dependencies between test statistics. Permutation testing, on the other hand, is an exact, non-parametric method of estimating the FWER for a given $\alpha$-threshold, but for acceptably low thresholds the computational burden can be prohibitive. In this paper, we show that permutation testing in fact amounts to populating the columns of a very large matrix $\PB$. By analyzing the spectrum of this matrix, under certain conditions, we see that $\PB$ has a low-rank plus a low-variance residual decomposition which makes it suitable for highly sub--sampled --- on the order of 0.5\% --- matrix completion methods. Based on this observation, we propose a novel permutation testing methodology, in [PDF] and [PDF], which offers a large speedup, without sacrificing the fidelity of the estimated FWER. Our evaluations on four different neuroimaging datasets show that a computational speedup factor of roughly $50\times$ can be achieved while recovering the FWER distribution up to very high accuracy. Further, we show that the estimated $\alpha$-threshold is also recovered faithfully, and is stable.
  
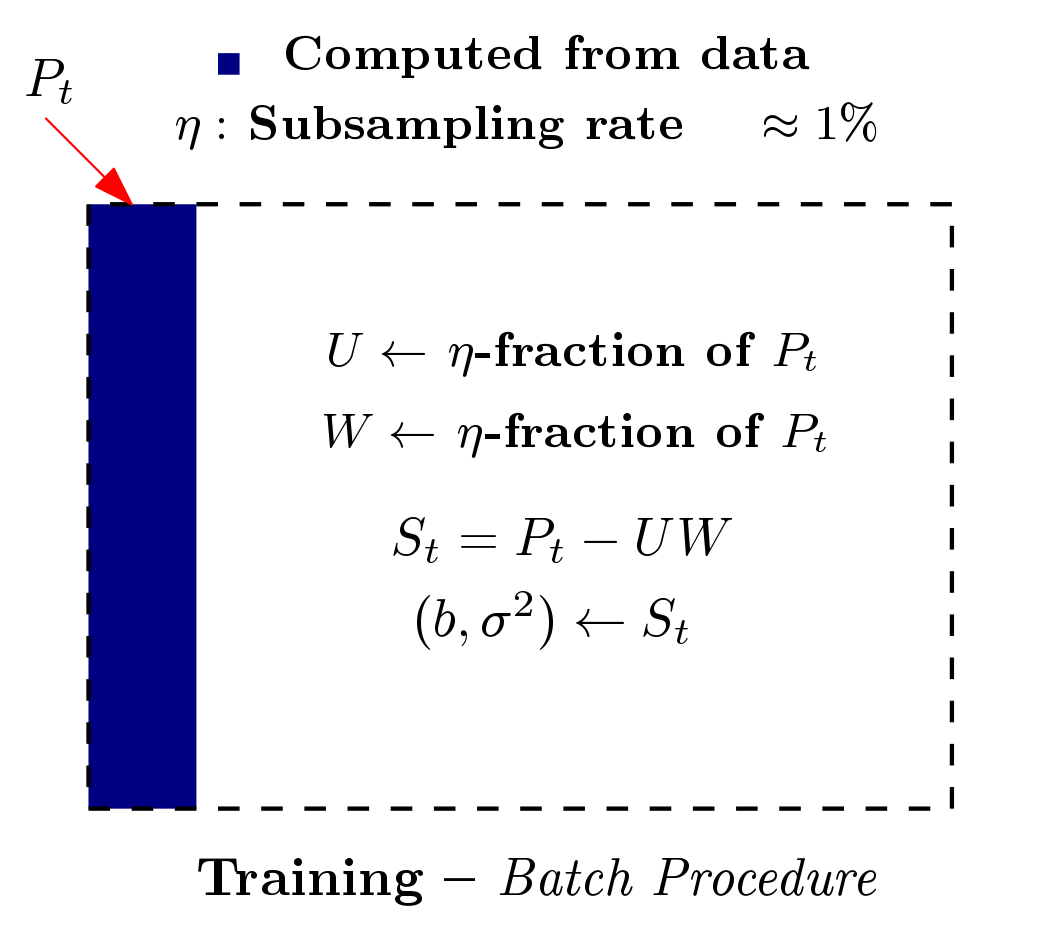
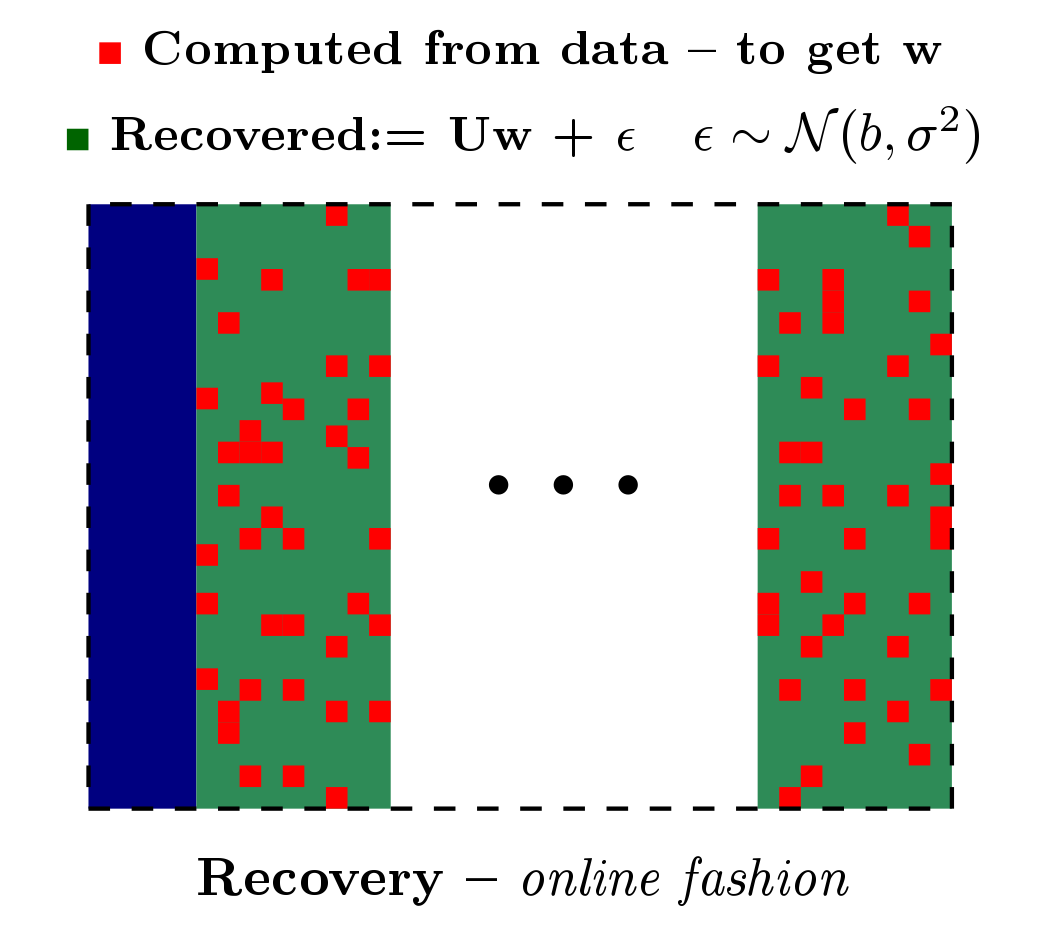
  Based on the work from [PDF] and [PDF], we built a patch, referred to as Rapid permutation testing (located here [RapidPT Tool]), for the widely-used nonparametric testing software (SnPM). This patch allows for very fast permutation testing in large (both data dimensionality and number of instances) medical studies.
  
  
• Wisconsin White Matter Hyperintensities Segmentation (W2MHS)   [Toolbox from NITRC]
  
  Precise detection and quantification of white matter hyperintensities (WMH) observed in T2-weighted Fluid Attenuated Inversion Recovery (FLAIR) Magnetic Resonance Images (MRI) is of substantial interest in aging, and age related neurological disorders such as Alzheimer's disease (AD). This is mainly because WMH may reflect comorbid neural injury or cerebral vascular disease burden. WMH in the older population may be small, diffuse and irregular in shape, and sufficiently heterogeneous within and across subjects. In [PDF] we pose hyperintensity detection as a supervised inference problem and adapt two learning models, specifically, Support Vector Machines and Random Forests, for this task. Using texture features engineered by texton filter banks, we provide a suite of effective segmentation methods for this problem. Through extensive evaluations on healthy middle-aged and older adults who vary in AD risk, we show that our methods are reliable and robust in segmenting hyperintense regions. A measure of hyperintensity accumulation, referred to as normalized Effective WMH Volume, is shown to be associated with dementia in older adults and parental family history in cognitively normal subjects. We provide an open source library for hyperintensity detection and accumulation (interfaced with existing neuroimaging tools), that can be adapted for segmentation problems in other neuroimaging studies.
  Based on the work from [PDF], we designed an open source MATLAB Toolbox (located at [W2MHS]) for detecting and quantifying White Matter Hyperintensities (WMH) in brain imaging studies.