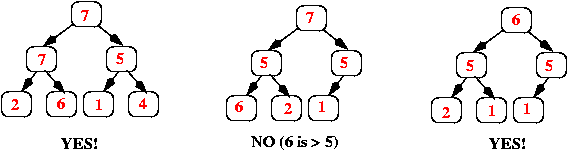
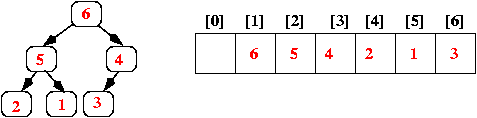
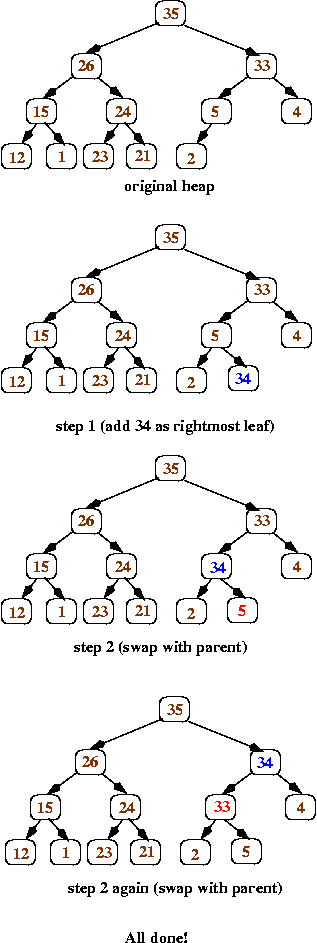
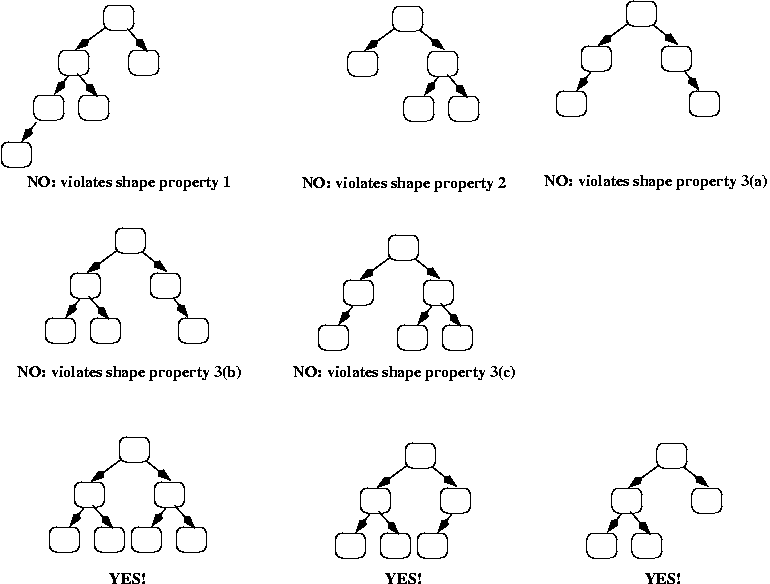Introduction
Here is a conceptual picture of a priority queue:

Think of a priority queue as a kind of bag that holds priorities. You can put one in, and you can take out the current highest priority. (Priorities can be any Comparable values; in our examples, we'll just use numbers.)
A priority queue is different from a "normal" queue, because instead of being a "first-in-first-out" data structure, values come out in order by priority. A priority queue might be used, for example, to handle the jobs sent to the Computer Science Department's printer: Jobs sent by the department chair should be printed first, then jobs sent by professors, then those sent by graduate students, and finally those sent by undergraduates. The values put into the priority queue would be the priority of the sender (e.g., using 4 for the chair, 3 for professors, 2 for grad students, and 1 for undergrads), and the associated information would be the document to print. Each time the printer is free, the job with the highest priority would be removed from the print queue, and printed. (Note that it is OK to have multiple jobs with the same priority; if there is more than one job with the same highest priority when the printer is free, then any one of them can be selected.)
The operations that need to be provided for a priority queue are shown in the following table, assuming that just priorities (no associated information) are to be stored in a priority queue.