Introduction
The previous set of notes discussed how to implement the List class using an array to store the items in the list. Here we discuss how to implement the List class using a linked-list to store the items. However, before talking about linked lists, we will review the difference between primitive and non-primitive types in Java.
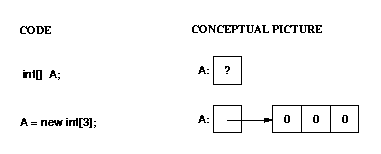
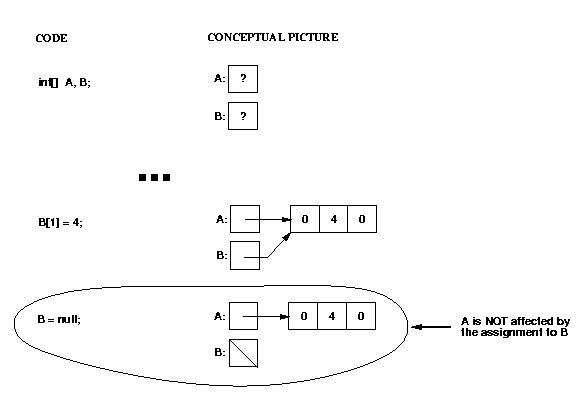
When you declare a variable with a reference type, you get space for
a reference (pointer) to that type, not for the type itself.
You must use "new" to get space for the type itself.
This is illustrated below.
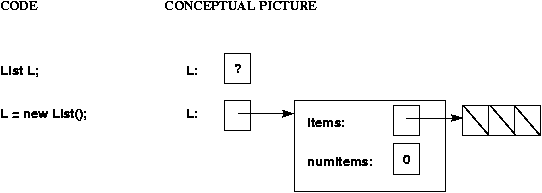
Remember that class objects are also reference types.
For example, if you declare a variable of type List, you
only get space for a pointer to a list; no actual list exists
until you use "new".
This is illustrated below, assuming the array implementation of lists,
and assuming that the List constructor initializes the
items array to be of size 3.
Note that because it is an array of Objects, each array element is
(automatically) initialized to null (shown using a diagonal line
in the picture).
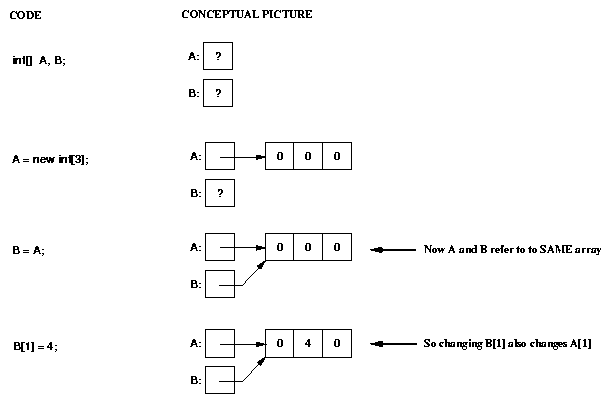
An important consequence of the fact that non-primitive types are really
pointers is that assigning from one variable to another can cause
aliasing (two different names refer to the same object).
For example:
Note that in this example, the assignment to B[1] changed not only that value,
but also the value in A[1] (because A and B were pointing to the same
array)!
However, an assignment to B itself (not to an element of the array pointed
to by B) has no effect on A:
A similar situation arises when a non-primitive value is passed as an
argument to a method.
For example, consider the following 4 statements, and the definition
of method changeArray:
Note that the method call causes A and X to be aliases
(they both point to the same array).
Therefore, the assignment X[1] = 10 changes both X[1]
and A[1].
However, the assignment X = new int[2] only changes X,
not A,
so when the call to changeArray finishes, the value of A[1]
is still 10, not 0.
For each line of the code shown below, draw the corresponding
conceptual picture.
Note that a linked list consists of one or more nodes.
Each node contains some data (in this example, item 1, item 2,
etc) and a pointer.
For each node other than the last one, the pointer points to the next
node in the list.
For the last node, the pointer is null (indicated in the example using
a diagonal line).
To implement linked lists in Java, we will define a Listnode
class, to be used to represent the individual nodes of the list.
To understand this better, consider writing code to create a linked
list with two nodes, containing "ant" and "bat", respectively, pointed
to by a variable named L.
First we need to declare variable L;
here's the declaration together with a picture showing what we have so far:
To make L point to the first node of the list, we need to use new to
allocate space for that node.
We want its data field to contain "ant" and (for now) we
don't care about
its next field, so we'll use the 1-argument Listnode
constructor (which sets the next field to null):
To add the second node to the end of the list we need to create the
new node (with "bat" in its data field and null in its
next field), and we need to set the next field of
the first node to point to the new one:
Assume that the list shown above (with nodes "ant" and "bat") has been
created.
Question 1.
Question 2.
And here's the code:
Note that it is vital to first copy the value of n's
next field
into tmp's next field (step 2(a)) before setting
n's next field to point to the new node (step 2(b)).
If we set n's next field first, we would lose our
only pointer to the rest of the list after node n!
Also note that, in order to follow the steps shown in the picture
above, we needed to use variable tmp to create the new node
(in the picture, step 1 shows the new node just "floating" there, but
that isn't possible -- we need to have some variable point to it so
that we can set its next field, and so that we can set
n's next field to point to it).
However, we could in fact accomplish steps 1 and 2 with a single
statement that creates the new node, fills in its data and
next fields, and sets n's next field
to point to the new node!
Here is that amazing statement:
Draw pictures like the ones given above, to illustrate what happens
when node n is the last node in the list.
Does the statement
Now consider the worst-case running time for this add operation.
Whether we use the single statement or the list of three statements,
we are really doing the same thing:
Note that the fact that n's next field
is still pointing to a node
in the list doesn't matter -- n has been removed from the list,
because it cannot be reached from L.
It should be clear that in order to implement the remove operation, we
first need to have a pointer to the node before node n
(because that node's next field has to be changed).
The only way to get to that node is to start at the beginning of the
list.
We want to keep moving along the list as long as the current node's
next field is not pointing to node n.
Here's the appropriate code:
Note that this kind of code (moving along a list until some condition holds)
is very common.
For example, similar code would be used to implement a lookup
operation on a linked list (an operation that determines whether there
is a node in the list that contains a given piece of data).
Note also that there is one case when the code given above will not
work.
When n is the very first node in the list, the picture is
like this:
In this case, the test (tmp.getNext() != n) will always be false, and
eventually we will "fall off the end" of the list (i.e., tmp will
become null, and we will get a runtime error when we try to dereference
a null pointer).
We will take care of that case in a minute;
first, assuming that n is not the first node in the list, here's the
code that removes n from the list:
How can we test whether n is the first node in the list, and
what should we do in that case?
If n is the first node, then L will be pointing to it,
so we can test whether L == n.
The following before and after pictures illustrate removing node n
when it is the first node in the list:
Here's the complete code for removing node n from a linked list,
including the special case when n is the first node in the list:
What is the worst-case running time for this remove operation?
If node n is the first node in the list, then we simply
change one field (L's next field).
However, in the general case, we must traverse the list to find the
node before n, and in the worst case (when n is the
last node in the list), this requires time proportional to
the number of nodes in the list.
Once the node before n is found, the remove operation involves
just one assignment (to the next field of that node), which
takes constant time.
So the worst-case time running time for this operation on a list with N
nodes is O(N).
Note that
if your linked lists do include a header node, there is no need for the
special case code given above for the remove operation;
node n can never be the first node in the list, so there
is no need to check for that case.
Similarly, having a header node can simplify the code that adds a node
before a given node n.
Note that if you do decide to use a header node, you must remember
to initialize an empty list to contain one (dummy) node, you must
remember not to include the header node in the count of "real" nodes in the
list (e.g., if you implement a size operation), and you must
remember to ignore the header node in operations like contains.
Look back at the definition of
the List class in
the first set of notes and think about which fields and/or methods
need to be changed before reading any further.
Clearly, the type of the items field needs to change, since the
items will no longer be stored in an array.
Instead, we will need to maintain a pointer to the first node in the list,
so the new declaration will be:
Given that change, let's think again about the three List methods
that were discussed assuming the array implementation:
The disadvantage of this approach is that it requires O(N) time to add a
node to the end of a list with N items.
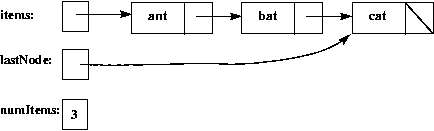
An alternative is to add a lastNode field (often called a
tail pointer) to the List class,
and to implement the methods that modify the linked list so that
lastNode always points to the last node in the linked list
(which will be the header node if the list is empty).
There is more opportunity for error (since several methods will need to
ensure that the lastNode field is kept up to date), but the
use of the lastNode field will mean that the worst-case running time
for this version of add is always O(1).
Here's a picture of the "ant, bat, cat" list, when
the implementation includes a lastNode pointer:
Write the "add at the end" method.
Below is a header for the "add at the end" method.
Write the method body.
Write the constructor.
In terms of ease of implementation, straightforward implementations of both
the array and linked-list versions seem reasonably easy.
However, the methods for the linked-list version seem to require more
special cases, and
achieving O(1) time for adding to the end of the list in the
linked-list version requires maintaining an extra pointer (to the last node).
Assume that lists are implemented using linked lists with just a
pointer to the first node in the list (no additional pointers),
and with no header node.
How much time is required (using Big-O notation) to remove the first
item from a list? to remove the last item from a list?
How do these times compare to the times required for the same
operations when the list is implemented using an array?
Another way to fix the problem is to use a doubly linked list.
Here's the conceptual picture:
Each node in a doubly linked list contains three fields:
the data, and two pointers. One pointer points to the previous node
in the list, and the other pointer points to the next node in the list.
The previous pointer of the first node, and the next pointer of the
last node are both null.
Here's the Java class definition for a doubly linked list node:
To remove a given node n from a doubly linked list,
we need to change the prev field of the node to its right,
and we need to change the next field of the node to its left,
as illustrated below.
Here's the code for removing node n:
The class definitions are the same as for the non-circular versions.
The difference is that, instead of being null, the next field of
the last node points to the first node, and (for doubly linked circular lists)
the prev field of the first node points to the last node.
The code given above for removing node n from a doubly linked list
will work correctly except when node n
is the first node in the list.
In that case, the variable L that points to the first node in the
list needs to be updated, so special-case code will always be needed
unless the list includes a header node.
Another issue that you must address if you use a circular linked list
is that if you're not careful, you may end up going round and round in
circles!
For example, what happens if you try to search for a particular value
val using code like this:
Write the correct code to search for value val in a circular
linked list pointed to by L.
(Assume that the list contains no "null" data values.)
The major advantage of doubly linked lists is that they make some operations
(like the removal of a given node, or a right-to-left traversal of the list)
more efficient.
The major advantage of circular lists (over non-circular lists) is that they
eliminate some special-case code for some operations.
Also, some applications lead naturally to circular list representations.
For example, a computer network might best be modeled using a circular list.
Java Types
Java has two "categories" of types:
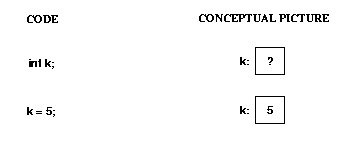
When you declare a variable with a primitive type, you get enough space
to hold a value of that type.
Here's some code involving a primitive type, and the corresponding
conceptual picture:
1. int[] A = new int[3];
2. A[1] = 6;
3. changeArray(A);
4. System.out.print(A[1]);
5. public static void changeArray(int[] X) {
6. X[1] = 10;
7. X = new int[2];
8. }
The picture below illustrates what happens when this code executes.

int [] X = new int[2];
X[0] = 1;
int Y = new int[3];
Y[0] = 2;
Y = X;
Y[0] = 3;
Intro to Linked Lists
Here's a conceptual picture of a linked list containing N items,
pointed to by a variable named L:

public class Listnode {
//*** fields ***
private Object data;
private Listnode next;
//*** methods ***
// 2 constructors
public Listnode(Object d) {
this(d, null);
}
public Listnode(Object d, Listnode n) {
data = d;
next = n;
}
// access to fields
public Object getData() {
return data;
}
public Listnode getNext() {
return next;
}
// modify fields
public void setData(Object ob) {
data = ob;
}
public void setNext(Listnode n) {
next = n;
}
}
Note that the next field of a Listnode is itself of type Listnode.
That works because in Java, every non-primitive type is really a
pointer;
so a Listnode object is really a pointer that is either null or points
to a piece of storage (allocated at runtime) that consists of two fields
named data and next.

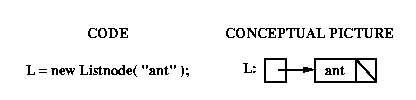

Write code to change the contents of the second node's data field from
"bat" to "cat".
Write code to insert a new node with "rat" in its data field
between the two existing nodes.
Linked List Operations
Before thinking about how to implement lists using linked lists,
let's consider some basic operations on linked lists:
Adding a node
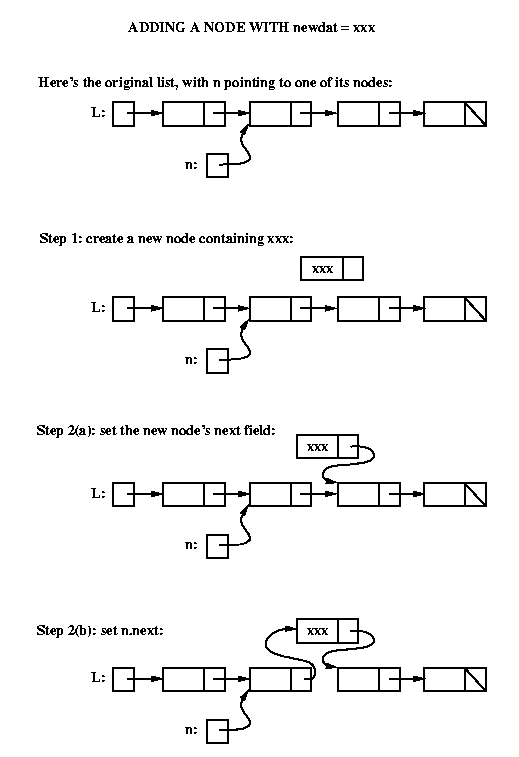
Assume that we are given:
and that the goal is to add a new node containing newdat immediately
after n. To do this we must perform the following steps:
Step 1: create the new node using the given data
Step 2: "link it in":
Here's the conceptual picture:
(a) make the new node's next field point to whatever
n's next field was pointing to
(b) make n's next field point to the new node.
Listnode tmp = new Listnode(newdat); // Step 1
tmp.setNext( n.getNext() ); // Step 2(a)
n.setNext( tmp ); // Step 2(b)
n.setNext( new Listnode(newdat, n.getNext()) ); // steps 1, 2(a), and 2(b)
n.setNext( new Listnode(newdat, n.getNext()) );
still work correctly?
We will assume that storage allocation via new takes constant time.
Setting the values of the three fields also takes constant time,
so the whole operation is a constant-time (O(1)) operation.
In particular, the time required to add a new node immediately after
a given node is independent of
the number of nodes already in the list.
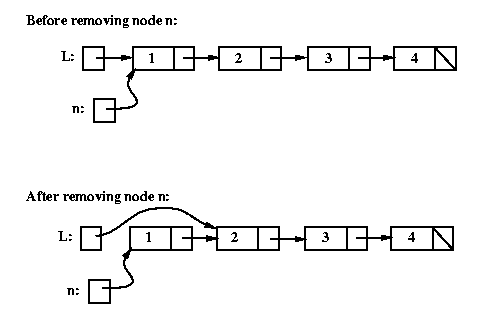
Removing a node
To remove a given node n from a linked list, we need to
change the next field of the node that comes immediately
before n in the list to point to whatever n's
next field was pointing to.
Here's the conceptual picture:

Listnode tmp = L;
while (tmp.getNext() != n) tmp = tmp.getNext(); // find the node before n

Listnode tmp = L;
while (tmp.getNext() != n) tmp = tmp.getNext(); // find the node before n
tmp.setNext( n.getNext() ); // remove n from the linked list
if (L == n) {
// special case: n is the first node in the list
L = n.getNext();
} else {
// general case: find the node before n, then "unlink" n
Listnode tmp = L;
while (tmp.getNext() != n) tmp = tmp.getNext();
tmp.setNext( n.getNext() );
}
Using a header node
There is an alternative to writing special-case code to handle removing
the first node in a list.
That alternative is to use a header node: a dummy node at the
front of the list that is there only to reduce the need for special-case
code in the linked-list operations.
For example, the picture below shows how the list "ant", "bat", "cat", would
be represented using a linked list without and with a header node:

The List Class
Now let's consider what changes need to be made to the definition of
the List class in order to change from the array implementation to the
linked-list implementation.
Remember, we only want to change the implementation (the "internal"
part of the list abstract data type), not the interface (the
"external" part of the abstract data type).
That means that the signatures of the public methods will not
change;
nor will the descriptions of what those methods do.
The only thing that will change is how the list is represented,
and how the methods are implemented.
private Listnode items; // pointer to the first node in the list of items
In the discussion below, we will assume that the linked list used to
store the items in the list does have a header node.
add (to end of list)
Recall that the first version of method add adds a given value
to the end of the list.
We have already discussed how to add a new node to a linked list following
a given node.
The only question is how best to handle adding a new node at the end
of the list.
A straightforward approach would be to traverse the list, looking for
the last node (i.e., use a variable tmp as was done above
in the code that looked for the node before node n).
Once the last node is found, the new node can be inserted immediately after it.
add (at a given position)
As discussed above for the "add to the end" method,
we already know how to add a node to a linked list after a given node.
So to add a node at position pos, we just need to find the
previous node in the list.
Since we're assuming that our List class is implemented with a header
node, there will always be such a node (i.e.,
we don't need any special-case code when we're asked to add a
node at the beginning of the list).
//**********************************************************************
// add
//
// Given: Object ob and int pos
//
// Do: Throw an exception if pos has a bad value.
// Otherwise, add ob to the list at position pos (counting from zero)
//
// Implementation:
// Check for a bad position and if so, throw an exception.
// Otherwise:
// If we're being asked to add to the end of the list,
// call the "add to the end" method (that way we don't need
// to worry about updating the lastNode pointer). Otherwise:
//
// o find the node n currently at position pos, counting the
// header node as being at position zero
//
// o create a new Listnode for ob, whose next field points to the
// node after n and set n's "next" field to point to the new node
//
//**********************************************************************
The List constructor
The List constructor needs to initialize the three List fields:
so that the list is empty.
An empty list is one that has just a header node, pointed to by both
items and lastNode.
As for the array implementation, numItems should be
set to zero.
Comparison: Lists via Arrays versus via Linked Lists
When comparing the list implementations using linked lists and using
arrays, we should consider:
In terms of space, each implementations has its advantages and disadvantages:
In terms of time:
Linked List Variations
There are several variations on the basic idea of linked lists.
Here we will discuss two of them:
Doubly linked lists
Recall that, given (only) a pointer to a node n in a linked list with
N nodes, removing node n takes time O(N) in the worst case,
because it is necessary to traverse the list looking for the node
just before n.
One way to fix this problem is to require two pointers: a pointer
the the node to be removed, and also a pointer to the node just before
that one.

public class DblListnode {
//*** fields ***
private DblListnode prev;
private Object data;
private DblListnode next;
//*** methods ***
// 3 constructors
public DblListnode() {
this(null, null, null);
}
public DblListnode(Object d) {
this(null, d, null);
}
public DblListnode(DblListnode p, Object d, DblListnode n) {
prev = p;
data = d;
next = n;
}
// access to fields
public Object getData() {
return data;
}
public DblListnode getNext() {
return next;
}
public Object getPrev() {
return prev;
}
// modify fields
public void setData(Object ob) {
data = ob;
}
public void setNext(DblListnode n) {
next = n;
}
public void setPrev(DblListnode p) {
prev = p;
}
}
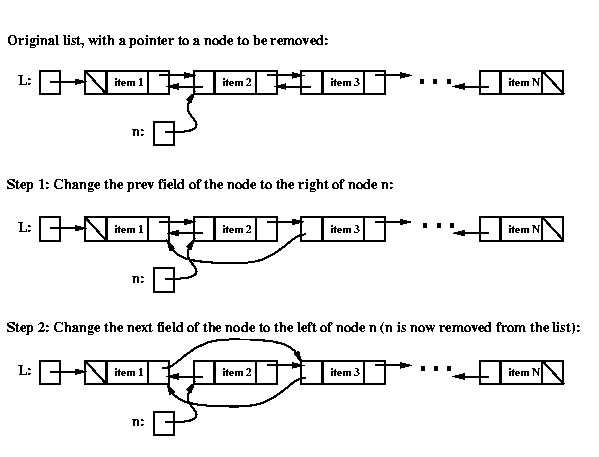
// Step 1: change the prev field of the node after n
DblListnode tmp = n.getNext();
tmp.setPrev( n.getPrev() );
// Step 2: change the next field of the node before n
tmp = n.getPrev();
tmp.setNext( n.getNext() );
Unfortunately, this code doesn't work (causes an attempt to dereference
a null pointer) if n is either the first or the last node in
the list.
We can add code to test for these special cases, or we can use a
circular, doubly linked list, as discussed below.
Circular linked lists
Both singly and doubly linked lists can be made circular.
Here are the conceptual pictures:

Listnode tmp = L;
while (tmp != null && !tmp.getData().equals(val)) tmp = tmp.getNext();
and the value is not in the list?
You will have an infinite loop!
Comparison of Linked List Variations
The major disadvantage of doubly linked lists (over singly linked lists)
is that they require more space (every node has two pointer fields instead
of one).
Also, the code to manipulate doubly linked lists needs to maintain
the prev fields as well as the next fields;
the more fields that have to be maintained, the more chance there is
for errors.


