CS/ECE 252 Introduction to Computer Engineering Spring 2011 All Sections Instructor: Andy Phelps TAs: Newsha Ardalani, Peter Ohmann, Jai Menon URL: http://www.cs.wisc.edu/~aephelps/courses/cs252/Spring2011/

Homework 3 // Due at lecture Mon, Feb 21

Primary contact for this homework: Peter Ohmann [ohmann at cs dot wisc dot edu]

You may do this homework with one other person from your section. You must put both names on the assignment. Please staple multiple pages together.

Problem 1 (2 points)

Draw a transistor-level circuit for a three-input AND gate.

Problem 2 (3 points)

1. Draw the gate-level representation for an eight-input multiplexer.
2. If you were to draw a 32-input multiplexer, how many select lines would be required?

Problem 3 (3 points)

1. Draw a gate-level circuit for the following logic expression. Do not simplify the expression. Your circuit must use 3 AND, 2 OR, and 2 NOR gates.
   
   Z = ((A AND B) OR (C AND D)) OR (NOT(A OR B) AND NOT(C OR D))
   
2. Find the truth table for this circuit.

Problem 4 (5 points)

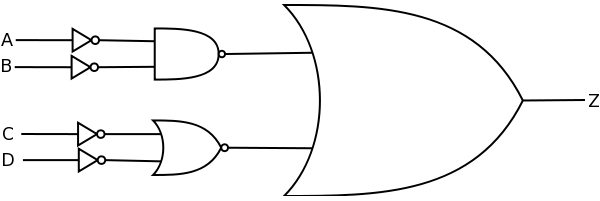
Given the circuit:

1. Draw the truth table.
2. Write the (unsimplified) logic expression.
3. Simplify the expression and redraw the circuit.
4. What principle (from the textbook) does this demonstrate?

Problem 5 (3 points)

Draw the FSM state-diagram for recognizing all 4-bit unsigned numbers greater than or equal to 12. (Hint: Each edge will either correspond to a 1 or a 0. If the last four bits correspond to a value greater than or equal to 12, your FSM should have 1 as output; otherwise, it should have 0). For help, look at the lock example in Figure 3.28 of the textbook (this is an extension of that example).

Update: Input is given the the FSM one bit at a time. Bits are given in left-to-right order (that is, higher-order bits come before lower-order bits). After consideration, you may provide an FSM that only reads EXACTLY 4 bits and performs as specified. If you do provide an FSM (slightly more complicated) which accepts based on the LAST FOUR bits, I will give extra credit.

Problem 6 (3 points)

How many memory locations can be addressed with a 16-bit address? Assuming the memory is byte-addressable and we are working with standard 32-bit integers, what is the theoretical maximum number of integers we could store and reference in our memory? (Hint: Think about how many total bytes/bits are in the memory). You may, of course, provide your answers as 2ⁿ.

Problem 7 (4 points)

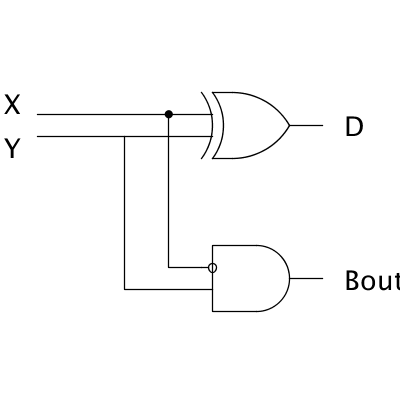
The figure below shows the gate-level circuit for a half-subtractor and its associated truth table. Similar to the full-adder, the full-subtractor takes two bits to be subtracted and a borrow-in, and outputs the result bit, and a borrow-out. Based on this and your knowledge of the full-adder:

X	Y	D (difference)	Bout (borrow-out)
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

1. Draw the truth table for a full-subtractor. Use columns X, Y, B_in, D, and B_out.
2. Draw the gate-level circuit for the full-subtractor.

Problem 8 (2 points)

If one begins with the R-S latch (Figure 3.18 in the textbook) and replaces the NAND gates with NOR gates, one obtains what is called an S-R latch. What impact will this have on the action of the latch?
Note: Your answer should include 2 changes--one relating to the input, and one to the output.