Minimum Spanning Trees in Java

What is a Minimum Spanning Tree?

A Minimum Spanning Tree (MST) is a subset of edges in an undirected, weighted graph that connects all vertices together with the minimum possible total edge weight, without creating any cycles.

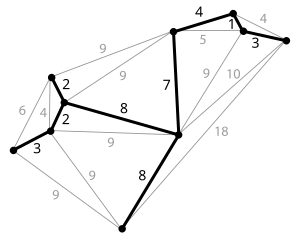
Example of a minimum spanning tree highlighted in a graph

MSTs have many real-world applications including:

Network design (e.g., designing road, telecommunications, or electrical networks)
Approximation algorithms for NP-hard problems
Cluster analysis in data mining
Image segmentation in computer vision

Common MST Algorithms

Kruskal's Algorithm

Kruskal's algorithm builds the MST by adding edges in order of increasing weight, skipping edges that would create a cycle.

Steps of Kruskal's Algorithm:

Sort all edges in non-decreasing order of their weight.
Initialize an empty MST.
Iterate through the sorted edges, adding each edge to the MST if it doesn't create a cycle.
Stop when the MST has (V-1) edges, where V is the number of vertices.

Implementation in Java:

public class KruskalMST {
    private static class Edge implements Comparable {
        int src, dest, weight;
        
        public Edge(int src, int dest, int weight) {
            this.src = src;
            this.dest = dest;
            this.weight = weight;
        }
        
        @Override
        public int compareTo(Edge other) {
            return this.weight - other.weight;
        }
    }
    
    private static class DisjointSet {
        int[] parent, rank;
        
        DisjointSet(int n) {
            parent = new int[n];
            rank = new int[n];
            
            for (int i = 0; i < n; i++) {
                parent[i] = i;
            }
        }
        
        int find(int x) {
            if (parent[x] != x) {
                parent[x] = find(parent[x]);
            }
            return parent[x];
        }
        
        void union(int x, int y) {
            int rootX = find(x);
            int rootY = find(y);
            
            if (rootX == rootY) return;
            
            if (rank[rootX] < rank[rootY]) {
                parent[rootX] = rootY;
            } else if (rank[rootX] > rank[rootY]) {
                parent[rootY] = rootX;
            } else {
                parent[rootY] = rootX;
                rank[rootX]++;
            }
        }
    }
    
    public static List findMST(List edges, int V) {
        Collections.sort(edges);
        List result = new ArrayList<>();
        DisjointSet ds = new DisjointSet(V);
        
        for (Edge edge : edges) {
            int x = ds.find(edge.src);
            int y = ds.find(edge.dest);
            
            if (x != y) {
                result.add(edge);
                ds.union(x, y);
            }
            
            if (result.size() == V - 1) break;
        }
        
        return result;
    }
}

Prim's Algorithm

Prim's algorithm builds the MST by selecting vertices, not edges. It starts from an arbitrary vertex and grows the tree by adding the cheapest edge connecting a vertex in the tree to a vertex outside the tree.

Key Features of Prim's Algorithm:

Better for dense graphs with many edges
Time complexity: O(E log V) with binary heap implementation
Does not require sorting of edges

Performance Comparison

The choice between Kruskal's and Prim's algorithms depends on the graph characteristics:

Algorithm	Time Complexity	Best for
Kruskal's	O(E log E) or O(E log V)	Sparse graphs
Prim's	O(E log V)	Dense graphs