Image Enhancement and Restoration

• Image Enhancement
  • Point Processing
  • Spatial filtering
  • Frequency domain enhancement
• Image Restoration

　　基本上，修改與修補的技術是很相近的，所用的方法大致都是希望藉由二維影像中某一個色點（pixel）他四周為的色點，來決定這個點應該有的顏色，通常我們把這個過程稱為 Filtering。透過 Filtering 的技術，大致而言我們可以把影像修改成我們希望的樣子，例如：把影像變得比較模糊或是比較銳利（sharpen），也可以把影像的對比調的更清晰，還可以把影像中物件的輪廓找出來﹍﹍等等。

　　就影像的修補（restoration）而言，我們是假設一張完美的影像，經過了某種形式的 filtering 之後，再加上一些雜訊（noise），最後變成了現在需要被修補的影像。而影像修補的技術，就是想辦法去猜測那是什麼形式的的 filtering 然後透過 inverse filtering 將影像還原。至於雜訊的部份，應為他的產生是很隨機的，故沒有什麼好方法可以將它去除。可想而知，這樣的修補所能達到的效果是相當有限的，若沒有專家的知識，是很難將影像回復到原本的風貌，所以以現在的技術程度而言，影像修補通常是由專家和電腦一起合力來完成。

※註(1)：為了說名的方便，以下的技術都是針對灰階的影像來做說明。

※註(2)：所有的數位影像都是二維的不連續函數，但為了說明的方便，我們常常先用假設他是連續的，找出它的特性，之後再把公式轉換成不連續的形式。

◎Image Enhancement

Notation:

• f(x): image, a 2D discrete function. F(x) is its Fourier transform.
• h(x): some 2D discrete function (maybe a filter) . H(x) is its Fourier transform.
• g(x): image after processing. G(x) is its Fourier transform.
• * : convolution operation. (It is the bridge between Spatial and Frequency domain method)

  

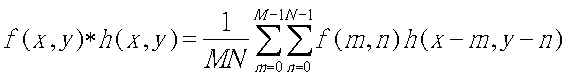
Classification:

• Spatial Domain Method
• Frequency Domain Method (Fourier transform)

Motivation:

• Spatial Domain mothod:

  Use the neighborhood of (x,y) to determine f(x,y)

  

  This example is make use the 8 neighbors to determine the central pixel. The method to determine could be a weighted sum of the 3x3 pixels, where the weight w1...w9 will determine which enhancement to perform.

• Fourier Domain method:

  1. Use high frequency to sharpen images.

  2. Use low frequency to blur images.

Point processing:

This method does not use any neighbor to enhance the image. It is just a functoion, which map one color to another one for each color. Although this method is so easy, it help a lot to make images clear.

• Intensity transformation:

  Example:

  

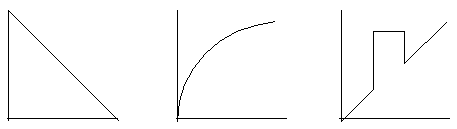
  x-axis : original color 　　y-axis : new color

  We can get a new image by applying these function to the original pixels. For example, the first function will produce a inverse image (black to white and white to black). The second function will make a dark picture bright. The third function will emphasis a special range of colors.

• Histogram processing:

  Histogram is used to represent "what percentage does a color have in the image." For example :

  

  x-axis : the colors in the image 　　y-axis : the probability the color occurs in the image.

• Histogram equalization :

  This is a kind of historgram processing to make low-contrast image high-contrast.

  

• Image Subtraction:

  Subtracting a special image to make the image more desired.

  g(x,y)=f(x,y)-h(x,y)

• Image Averaging:

  Averaging a lot of noisy images which have the same content will delete the noise.

Spatial Filtering :

Use the neighbors of some pixel to determine the pixel. For example:

Derivative filters will find the edge of an object.

Examples :

Original image :

Its histogram of luminance :

Its histogram of Red :

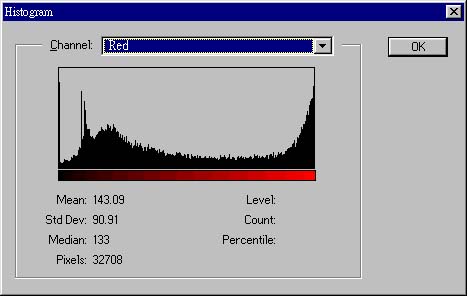
Its histogram or Green:

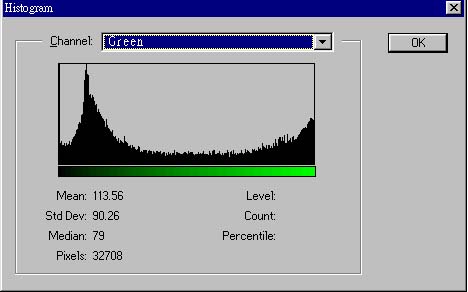
Its histogram of Blue:

After lowpass fitlering:

After highpass filtering:

After Sobel (Derivative) filtering:

　　　

merge the above pictures result edges of object:

Frequency Domain Enhancement :

• Motivation:

  Edges , sharp transitions and other abrupt changes in gray levels are associated with high-frequency components.To sharpen: emphasize high-frequency components.To blur: emphasize low-frequency components.

  Equation: G(u,v) = H(u,v)F(u,v)

  G(u,v) is the new image, F(u,v) is the original image, H(u,v) is the filter.

• Lowpass filtering:

  

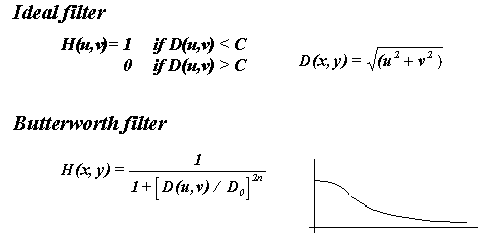
• Highpass filtering:

  

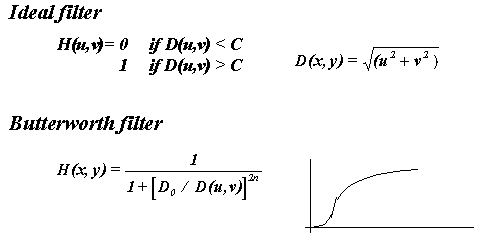
• Frequency domain method vs. Spatial domain method:

  

  

◎Image Restoration

Goal:

• Restore the damaged originals:
• Restore the damaged image because of imperfect acquisition: noise, quantization or geometric transformations.

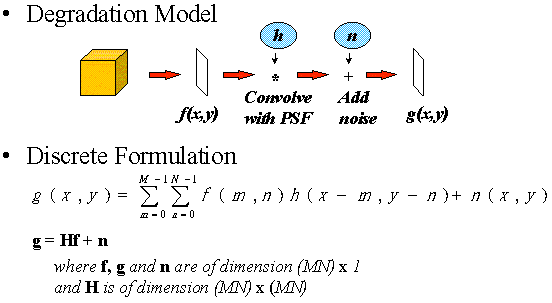
Degradation Model:

g(x,y)=H[f(x,y)]+n(x,y)

where g(x,y) is the damaged image, f(x,y) is the perfect image, n(x,y) is a random noise function, H is some transformation operation.

Assumption: H is linear and position invariant.

• H[mf(x.y)+ng(x,y)]=mH[f(x,y)]+nH[g(x,y)]
• H[ f(x-a,y-b) ]=H[f](x-a,y-b)

Point Spread Function:

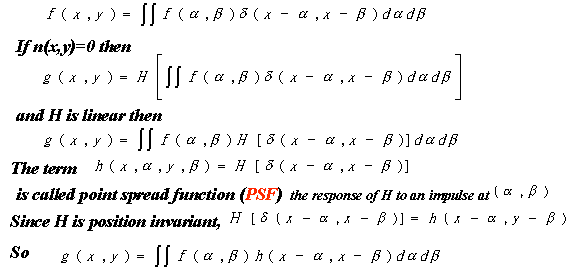
Methods:

• Inverse filtering:

  

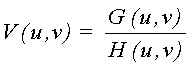
  1. Compute the 2D FFT of image g, called G.
  2. Compute the 2D FFT of PSF h, called H.
  3. Compute the new image V(u,v)=G(u,v)/H(u,v).
  4. Compute the inverse FFT of V.

• other methods: