Successive Numeric Approximation

Terminology

successive numeric approximation : process of solving a mathematical problem using a numeric algorithm that estimates a solution
        one estimate leads to the next (hopefully better) estimate

convergence : Does the algorithm always produce the correct answer? Do estimates get better?

rate of convergence : How fast does the algorithm come up with a "good" estimate?

error =

percentage error =

estimated error =

step size (h) : value set at beginning of algorithm

order of accuracy :

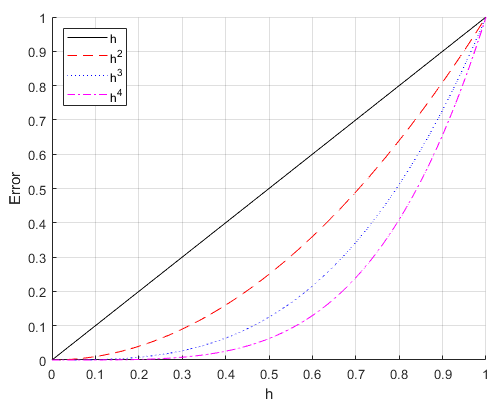
Comparing h, h^2, h^3, h^4 over h = 0 .. 1

O(h) - linear :
 

O(h2) - quadratic :
 

O(h3) - cubic :
 

Finding roots using Newton's method

Find the value(s) of x such that f(x) = 0

Newton's Method

 

 

 

 

Example: find the roots of f(x) = 6 - 2x2

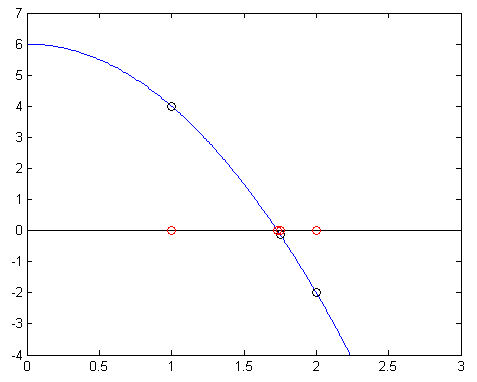
Figure for demonstrating Newton's method

 

 

 

 

 

 

 

 

 
x(1)    = 1
x(2)    = 2
x(3)    = 1.75
x(4)    = 1.7321428571428572
x(5)    = 1.7320508100147276
x(6)    = 1.7320508075688772
x(7)    = 1.7320508075688774
x(8)    = 1.7320508075688772
x(9)    = 1.7320508075688774
x(10)   = 1.7320508075688772

sqrt(3) = 1.7320508075688772

Numerical integration

 

Trapezoid Method

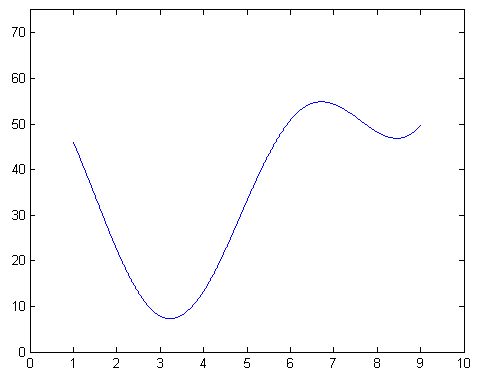
curve to integrate

Simpson's Method

curve to integrate

Numerically estimating the derivative

The following function that estimates the derivative of the function fctn at the value x (using a step size of h):

function dfdx = derivative(fctn, x, h)
dfdx = (fctn(x+h) – fctn(x))/h;

How good of an estimate is this?

Consider the function f(x) = cos(x) + 2x
We know the derivative is f '(x) = -sin(x) + 2

How does the error change over an interval?

Consider the following code:

fctn = @(x)cos(x) + 2*x;
fprime = @(x)-sin(x) + 2;

xx = 0 : 0.01 : 20;
dyy = derivative(fctn, xx, 0.1);
exactDyy = fprime(xx);

errors = abs(fprime(xx) - dyy);
percErrors = errors./fprime(xx)*100;

plot(xx, percErrors)
title('Percent error of derivative estimate')
xlabel('x')
ylabel('% error')

How does the error change as h changes?

Consider the following code:

for k = 1 : 4
    h(k) = 10^(-k);
    dyy = derivative(fctn, xx, h(k));
    
    errors = abs(fprime(xx) - dyy);
    percErrors = errors./fprime(xx)*100;
    
    meanErrors(k) = mean(percErrors);
    maxErrors(k) = max(percErrors);
    minErrors(k) = min(percErrors);
end

and the results it calculates:

h       meanErrors  maxErrors   minErrors 
0.1000  1.79635296  2.94200783  0.00157170
0.0100  0.18001463  0.28923021  0.00015739
0.0010  0.01800492  0.02887305  0.00002315
0.0001  0.00180053  0.00288680  0.00000212