]> Exercises

Exercises

Find the area between the two curves

    Use Commands not the right-click menus.

  1. Find the area between the curves, sin(x) and cos(x)
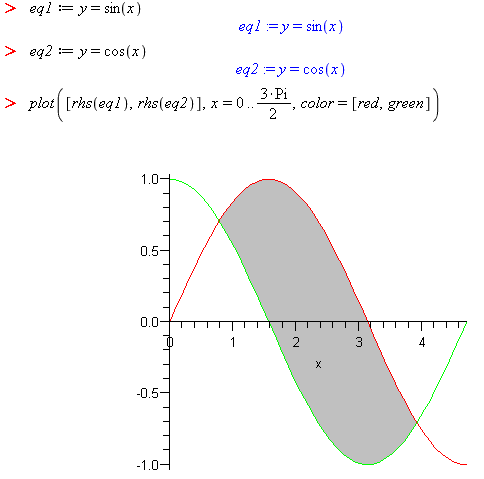
    two intersection points in range x=0..3*Pi/2

    Use fsolve to find the specific points of intersection for which we are interested.
    area between the curves cos(x) ans sin(x) is 2.828427125

  2. Find the area between these two curves.

    y= ( x+2 ) 3 +5 y=−3 x 2 +13 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqr1ngBPrgifHhDYfgasaacH8YjY=vipgYlh9vqqj=hEeeu0xXdbba9frFj0=OqFfea0dXdd9vqai=hGuQ8kuc9pgc9q8qqaq=dir=f0=yqaiVgFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWG5bGaeyypa0ZaaeWaaeaacaWG4bGaey4kaSIaaGOmaaGaayjkaiaawMcaamaaCaaaleqabaGaaG4maaaakiabgUcaRiaaiwdaaeaacaWG5bGaeyypa0JaeyOeI0IaaG4maiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaaIXaGaaG4maaaaaa@4853@ 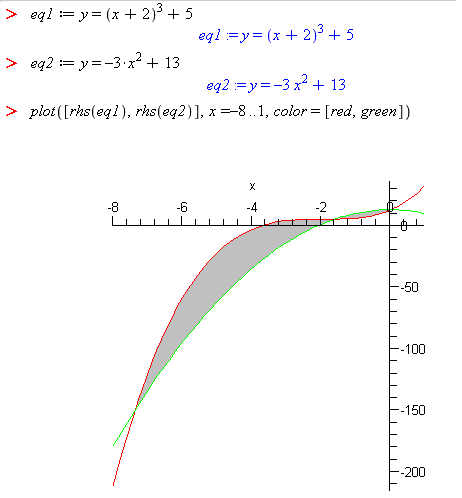area between the curves is shaded. There are two parts (three intersection points).

    In this case, eq1 is a 3rd degree polynomial and eq2 is a second degree polynomial. A 3rd degree polynomial may intersect a line or 2nd degree polynomial in 0, 1, 2, or 3 points.

    Use the solve command (or fsolve if necessary) to find the points of intersection.
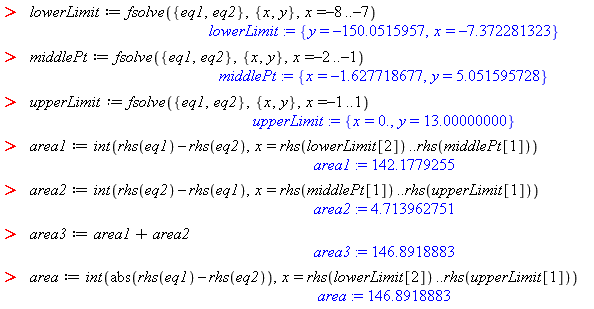
    area between the curves is 2.828427125

    Notice that computing the area in two steps or integrating the absolute value of the difference between the lower and upper limit both compute the same area between the two curves.