Examples:
The simplest imaginable integral gives Maple trouble when the assume command is not used.
e1 := x^m
int(e1, x=0..1)
Comment: The result is returned as a limit. This is correct because if m+1 is negative, then the integral is infinite. However, this is not likely what you meant. So assume m+1 is non-negative and try again.
assume(m >= -1)
int(e1, x=0..1)
Comment: Now the result is quite simple. The ~ after the parameter, m, signifies that it has assumed properties.
The integral can be done over arbitrary symbolic limits.
int(e1, x=a..b)
Comment: The result is returned in terms of a and b. Numerical values for a and b can be substituted to complete the integral for different pairs of limits.
i1 := sin(x)
int(i1, x)
int(i1, x=0..Pi)
i2 := sin(n*x)
plot([sin(x),sin(2*x), sin(3*x),sin(4*x)], x=0..Pi)
int(i2, x)
int(i2, x=0..Pi)
assume(n, integer)
int(i2, x=0..Pi)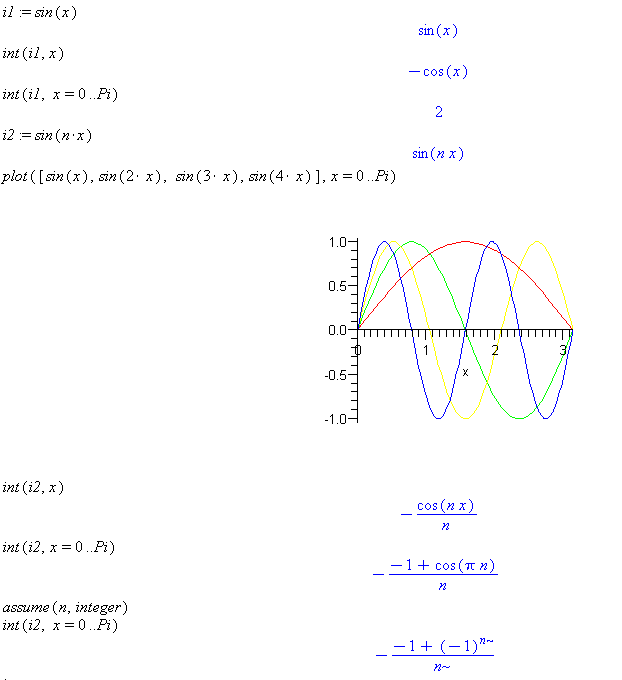
Comment: Maple has no trouble doing the indefinite integrals, but the definite integrals are left in terms of the cosine function. By telling Maple that the parameter n is an integer, it gives a simpler result to the definite integral. Before doing this, Maple returned the general result for n being any real number.
f1 := exp(-a*x) * cos(b*x)
assume(a>0)
f1int := int(f1, x=0..infinity)
simplify(f1int)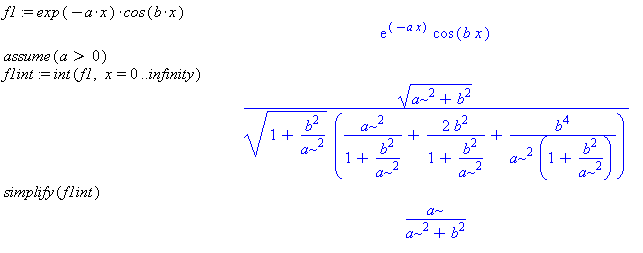
Comment: This definite integral has a finite value only for values of positive a. Therefore the assume command must be used in order to do the integral. The simplify command greatly simplifies the result in this case.
A famous function is sin(x)/x. You might think the integral of this function is infinite because of the x in the denominator. However, this integral has a finite value. This integral is important in wave diffraction and signal processing.
int(sin(x)/x, x=0..infinity)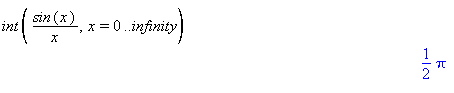
Comment: This integral is not doable using standard calculus substitutions. It is remarkable that Maple can find the integral.
A very complex integrand is given below.
int(exp(-x^2)*cos(p*x), x=-infinity..infinity)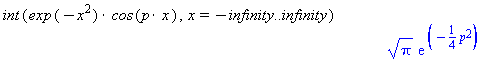
Comment: Again, this integral is not doable using standard calculus substitutions. So once again Maple defies belief in its abilities to do integrals!

