Examples:
e3 := x^2 + 2*x + 1
int(e3, x=0..4)
Comment: Notice that the result is returned as a rational fraction because Maple does the integral symbolically.
e4 := cos(x)
plot(e4, x=0..Pi)
e4int := int(e4, x=0..Pi)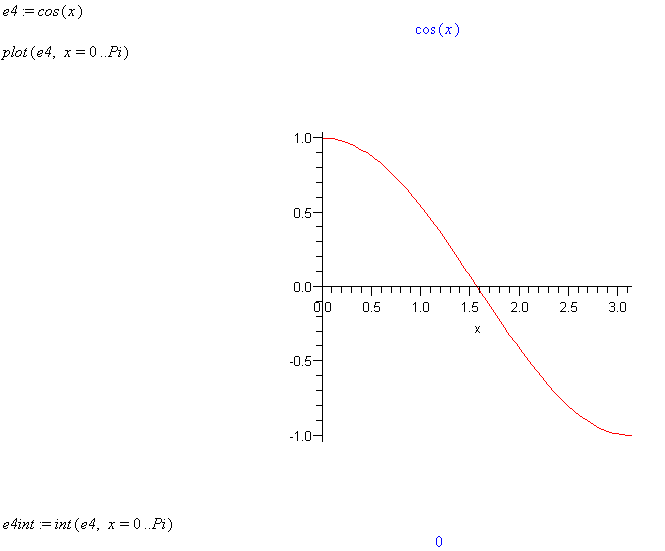
Comment: In this case the area below the x-axis is considered negative so the total integral is zero between these limits.
e5 := (1+x^4-2*x^5)/(1-x^8)
inte5:= int(e5, x=0..2)
evalf(inte5)
Comment: This integral required partial fraction representation to integrate across the singularity at x=0. Maple did this with ease!
You have just bought an interesting bucket at a yard sale and would like to set it up to collect rain water to measure how much is falling. The only problem is that this bucket is not marked. The function for the volume of the bucket is
where h is the height of the water in the bucket. The following commands will find the volume for a general height so you can easily mark the volume in your bucket for the height of water.
ex6:= 2*Pi*x*(x-1)^2
vol:=int(ex6, x=0..h)
Comment: This a “real world” use of definite integration with a symbolic limit. Maple solved the integral and assigned it to vol, which means finding the value of vol at any h is easy.

