Examples

1. Find the value of the maximum volume of a cone with a slant height equal to 1 (Type the Maple commands)

   

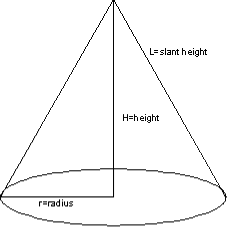
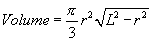
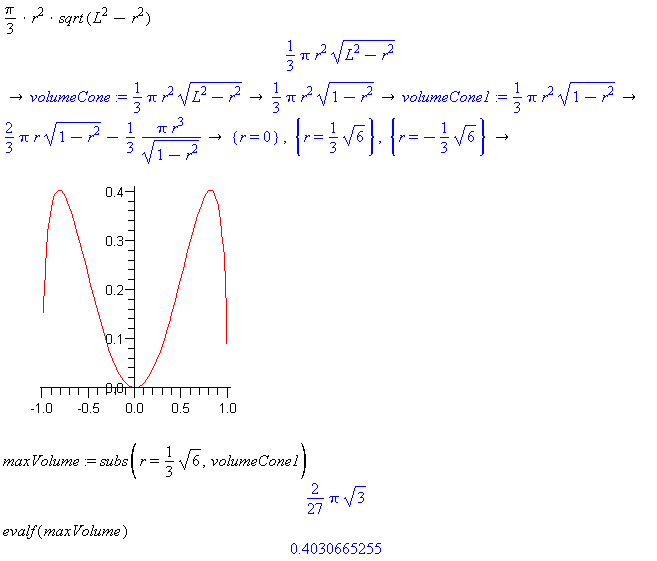
   Find the maximum volume of the cone above, using the formula for cone volume and L=1.

   

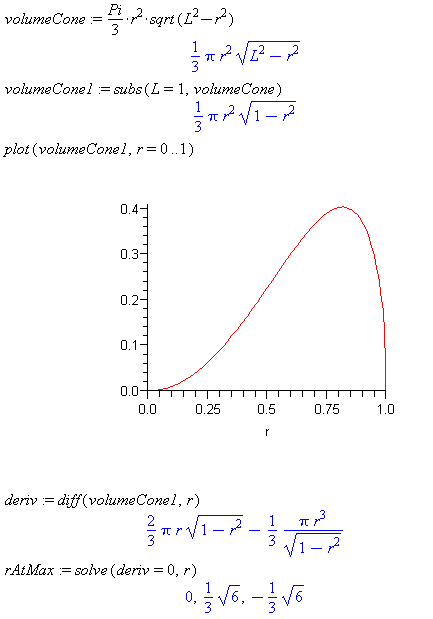
   The positive solution is the only reasonable solution for this problem. Thus, find the max volume by substituting the third root that was found.

   Note: If you try to "solve" an expression in Maple, Maple will turn that expression into an equation by setting the expression equal to zero. Thus the last command could be replaced by: rAtmax:=solve(deriv,r) and it would still work.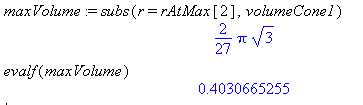

   

2. Find a formula for the maximum volume of a cone in terms of its slant height

   Hint: Perform the same procedure as before but do not substitute L=1.

   

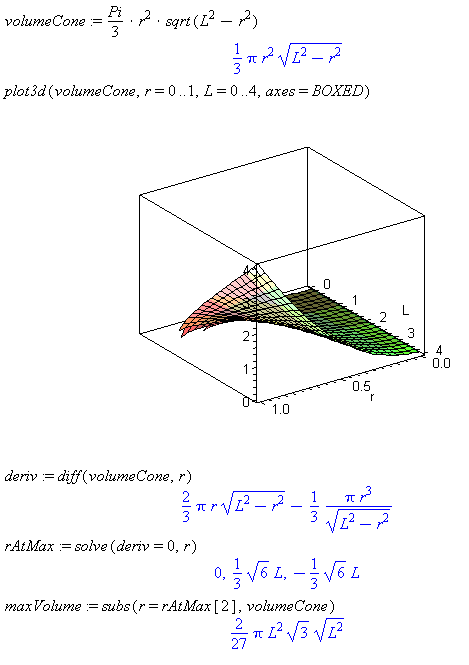
   Comment: Solving the problem in this way gives a formula for the result that can be used to find the max volume for any slant height. Substitute the for L to find the maxVolume.

   

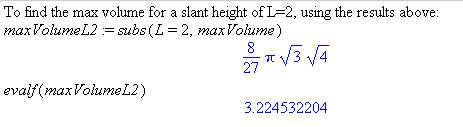
   But, what if you also need to know the radius for that slant height? First, use the formula for rAtMax to calculate the correct radius for the given slant height.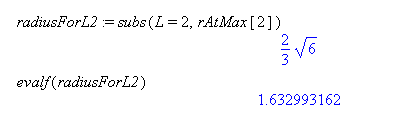

   

3. Find the maximum volume of a cone with slant height equal to one (Try the Right Click Menu)

   

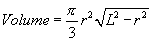
   Find the maximum volume of the cone above, using the formula for cone volume and setting L=1

   These steps will complete this problem:

   1. Enter and assign the name volumeCone to the formula given in the problem.
   2. Evaluate the volume at L=1 and assign the result the name volumeCone1.
   3. Plot the new formula for the volume of a cone with slant height L = 1. Notice the existance and approximate location of any maxima and minima.
   4. Compute the derivative of the volumeCone.
   5. Solve the resulting derivative to find the roots (values) that could produce the maximum volume. Notice, that Maple's solve command automatically sets expressions equal to 0.
   6. Consider the solutions and recognize that only a positive value for a radius made sense.