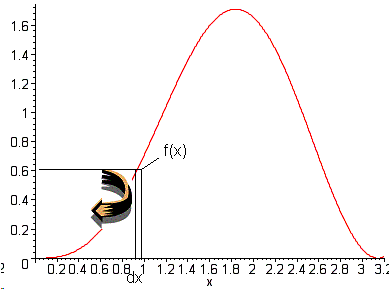
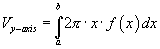Volumes of revolution
A common application of integration is computing the volume of revolution. This is where a function is rotated around either the x or y axis to form a solid volume. You know from calculus that the volume is pictured conceptually as either an infinite stack of infinitesimally thin coins with radii defined by the function for rotation around the x axis or as an infinite set of nested cylindrical shells of infinitesimal thickness with the function defining the height of the shell for rotation around the y axis.
For rotation around the x-axis we use:
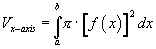
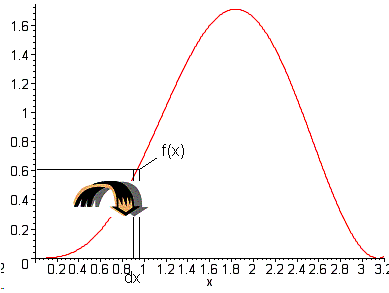
For rotation around the y-axis we use: