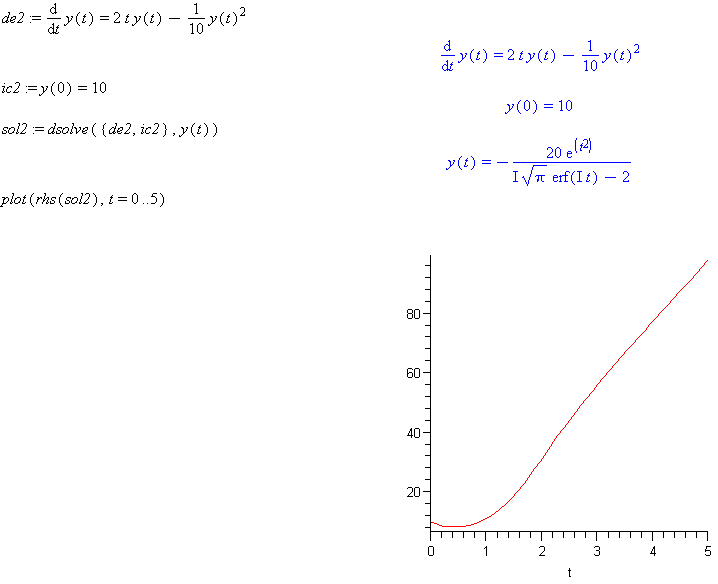Exercises

Solve each ODE both analytically and numerically. Also, plot the analytical and numerical solutions.

1. $\frac{dy}{dt}=2ty\text{ y(0)=10}$

   Hint: The solution changes quickly, choose your range of t for the plot carefully.

   To get the analytical solution

   

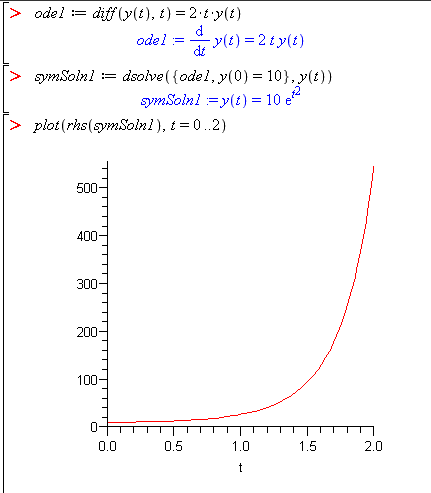
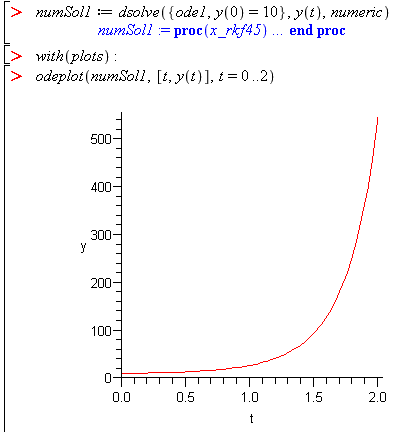
   Note: I had to plot from 0 to 2 because if you set the range beyond a certain point y is increasing so fast that Maple can not plot the values. Also, there isn't additional behavior detail when plotting over a larger range.

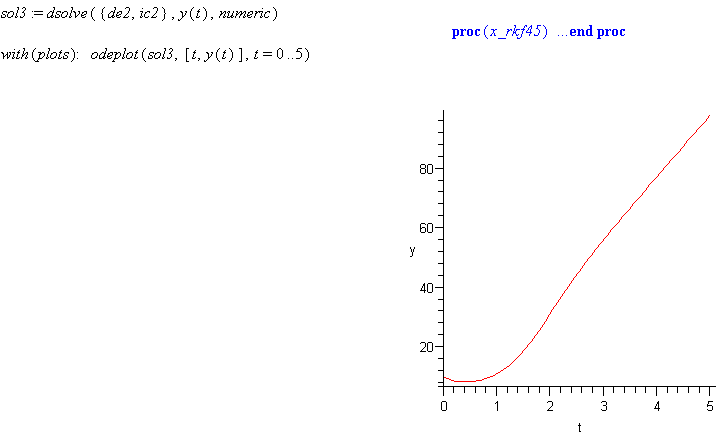
   To get the numerical solution

   

2. $\frac{dy}{dt}=2ty-\frac{y{(t)}^2}{10}y(0)=10$

   To get the analytical solution

   

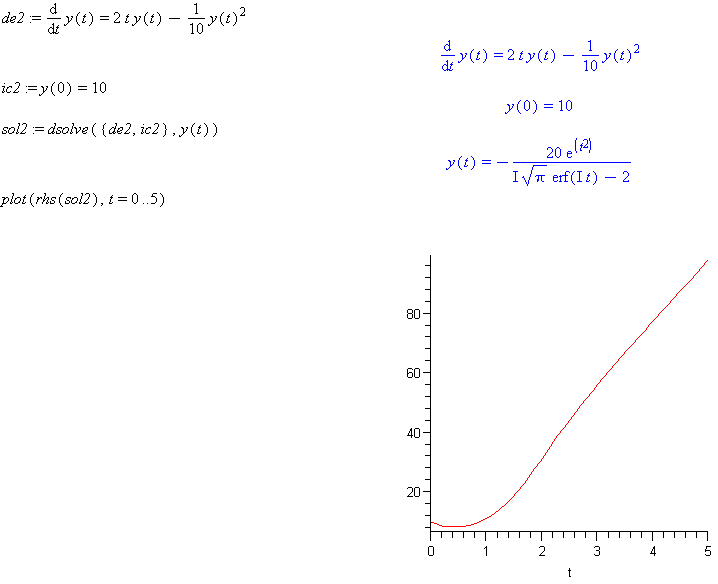
   To get the numerical solution