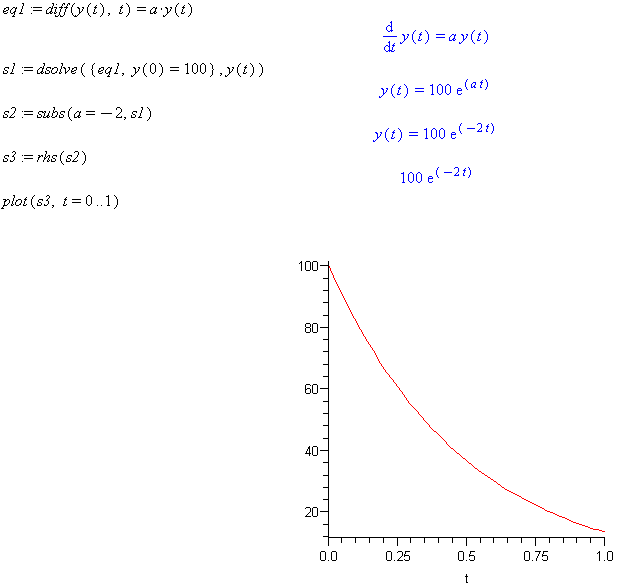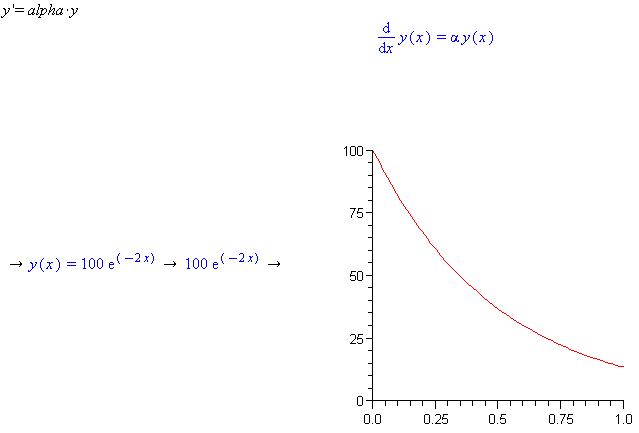Exercises

Solve the ODE: $\frac{dy(t)}{dt}=\alpha y(t)$ with the given conditions and stipulations and plot the solutions

1. alpha= -2
   y(0)=100
   Use commands to solve the problem.

   eq1:=diff(y(t), t) = a*y(t)
s1:=dsolve({eq1, y(0)=100},y(t))
s2:=subs(a=-2, s1)
s3:=rhs(s2)
plot(s3, t=0..1)

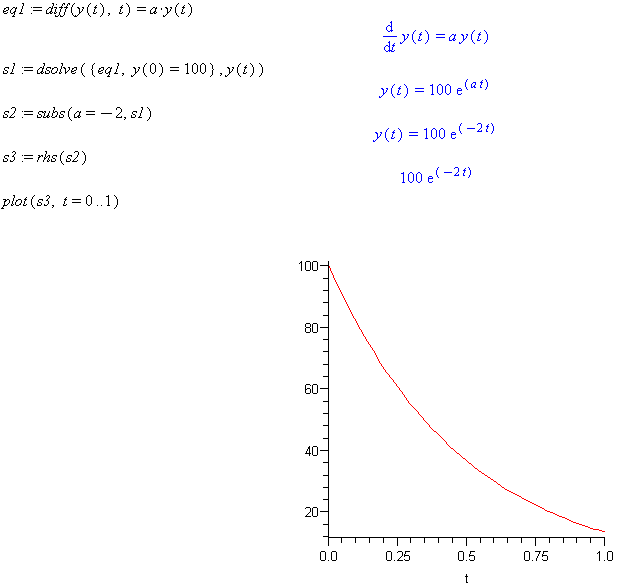
2. alpha= -2
   y(0)=100
   Use right-clicks to solve the problem.

   Now we will do the same problem but use right-click instead.
   Enter: y'=alpha*y
   Right-click and select solve DE interactively
   Click edit under the Conditions box and enter 0 and 100 so the top reads y at 0=100 and then click edit under parameters and enter -2 for alpha
   Now click Solve Symbolically
   Click Solve on the top right of the window that opens and then on the bottom left select 'on Quit, Return Solution'
   Now click Quit in the bottom right
   Right click the returned solution and hit Right-Hand Side
   Right click and select plot->2D
   Right click and change the range to 0 to 1 for the x and make appropriate changes to the y axis.
   

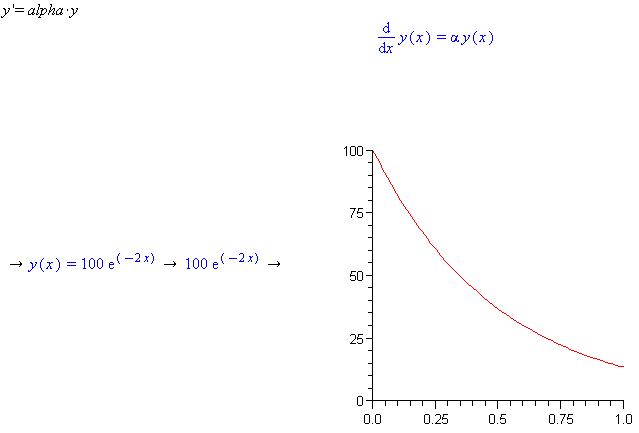
The following questions do not require Maple.

1. Is this a linear first order ODE?
   $\frac{df}{dt}-\cos \left(\alpha t\right)=f$

   YES because the unknown function f(t) appears only to the first power. But be careful to first rearrange the ODE in our notation in the discussion. Thus $p\left(s\right)=-1,g\left(s\right)=\cos \left(\alpha t\right)$

2. What is the solution of the following linear first order ODE?
   $\frac{df}{dt}=7-3f,f\left(0\right)=5$

   Solution: Put the equation in our preferred notation and identify p(s) and g(s).
   $\frac{df}{dt}+3f=7,f\left(0\right)=5,p\left(s\right)=3,g\left(s\right)=7$
   $\begin{array}{l}u\left(t\right)=\exp \left[{\displaystyle {\int }_{t}p\left(s\right)ds}\right],p\left(s\right)=3\\ u\left(t\right)=\exp \left[{\displaystyle {\int }_{t}3ds}\right]=\exp \left[3t\right]\\ \frac{1}{u\left(t\right)}=\exp \left[-3t\right]\end{array}$
   Next
   ${\displaystyle {\int }_{t}u\left(s\right)g\left(s\right)ds}+c={\displaystyle {\int }_t\exp \left[3t\right]\left(7\right)ds}+c=\frac{7}{3}\exp \left[3t\right]+c$
   Putting this together
   $f\left(t\right)=\exp \left[-3t\right]\left\{\frac{7}{3}\exp \left[3t\right]+c\right\}$ or $f\left(t\right)=\left\{\frac{7}{3}+c\exp \left[-3t\right]\right\}$
   Now use the initial condition to find the constant c.
   $f\left(0\right)=5,f\left(0\right)=\left\{\frac{7}{3}+c\exp \left[0\right]\right\}=5$
   $\frac{7}{3}+c=5\Rightarrow c=\frac{8}{3}$ . Thus $f\left(t\right)=\frac{1}{3}\left\{7+8\exp \left[-3t\right]\right\}$