CS/ECE 252 Introduction to Computer Engineering Spring 2008 All Sections Instructor David A. Wood TAs Spyridon Blanas, Priyananda Shenoy & Shengnan Wang URL: http://www.cs.wisc.edu/~david/courses/cs252/Spring2008/

Homework 1 // Due at lecture Wed, Jan 30

Primary contact for this homework: Spyros Blanas [sblanas at cs dot wisc dot edu]

You must do this homework alone. Please staple multiple pages together.

Problem 1

1. What is the web address of the course home page? (should be http://...)
2. What is the email address of your section's mailing list? (should be in the "To:" field of any correspondences you receive)

Problem 2

If you turn in a homework late, should you expect 0 points or ask for an exception? Why or why not?

Problem 3

(This question has no wrong answers.)

1. What is your expected major(s)?
2. Have you taken any other CS courses in the past? If yes, please list them.
3. Why are you taking this course?
4. What do you hope to get out of it?

Problem 4

Consider the question "What is the meaning of life, the universe and everything?"

1. Can a digital computer answer this question? Why or why not?
2. Suppose that there is a digital computer system which can answer this question. We run the following experiment 20 times:
   1. We reset the computer to a specific state.
   2. We ask the question.
   How many different answers will we get?

Problem 5

Give one example of an analog device and one of a digital device.

Problem 6

Newspaper headline: I.B.M. Gets $225 Million Contract for Weather Supercomputer (source: New York Times, June 1, 2002.)

Why pay millions of dollars for a new computer? Can't a supercomputer compute exactly the same things a small and cheap computer can?

Problem 7

Assume that you have an unlimited number of "black boxes" which take two numbers x, y as input and output their sum: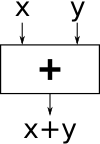

We want to calculate the sum of four numbers, i.e. a+b+c+d, using any number of these boxes.

1. Show two different ways to do that.
2. How many boxes did you use in each design?
3. Consider the path which connects an input to the output. (For this problem, there are four such paths for each design.) What is the maximum number of boxes found on every path, for each design?