|
My UW
|
UW Search
Computer Science Home Page
> ~david/courses
Home
Contact Info
Lecture & Notes
Schedule
LC-3 Simulator
Grading
Examinations
Homework
|
 |

|
|
Homework 2 // Due at lecture Friday Feb 8
Primary contact for this homework: Priyananda Shenoy [shenoy at cs.wisc.edu]
You must submit your solutions in paper(no soft copies).
Please be sure to include your name, email address and your section.
You must do this homework alone.
Please staple multiple pages together
Helpful hint: Show all the intermediate steps for your answers. That way we can
give you partial credit even if you get the answer wrong
Problem 1
a) Suppose that the total number of students in some class is 224. If each student is assigned a unique bit pattern, what is the minimum number of bits required to do this?
b) Suppose that for Section 1 of this class, we need 8 bits to represent everyone uniquely. Similarly for Section 2, we need 7 bits. If both sections are combined into one big section, how many bits are required to represent everyone uniquely?
Problem 2
Interpret the following 8-bit sequence '10110010' as the following:
a) unsigned integer
b) signed magnitude integer
c) 1's complement integer
d) 2's complement integer
Specify the answer in decimal.
Problem 3
The range of a representation is the set of values which can be represented using that representation. For example, if an integer is represented by 5 unsigned bits, then its range is 0 to 31. What is the range of an integer represented in 8-bit 2's complement form?
Problem 4
Let X = 101010, Y = 110011 and Z = 011101. Then evaluate the following:
a) (X OR Y) AND Z
b) X OR (Y AND Z)
c) (X OR Y) AND (X OR Z)
Problem 5
Convert the following bit sequence into hexadecimal
1111101011001110000011111111
Problem 6
Write the decimal equivalents for these IEEE floating point numbers.
a. 0 01010111 00000000000000000000000
b. 1 01111010 10000000000000000000000
Problem 7
Translate the following ASCII codes into a string of characters by interpreting each group of eight bits as an ASCII character:
0x5448495320495320535041525441
(0x20 is the 'space' character)
Problem 8
Consider an operation CLEAR-EVEN-BITS which takes in an input bit sequence and gives as output the following sequence:
a) all even bits of the output(0th bit, 2nd bit etc) are set to 0
b) all odd bits of the output are the same as the corresponding input bits.
For example, if input is 11001011, then output is 10001010. See image below for clarifications
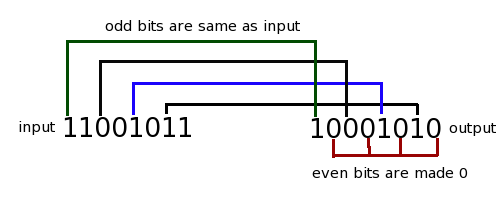
Implement this operation using any of NOT,AND,OR. Assume that the input is always 8-bits long. The 0th bit is the right most bit.
(hint:Your answer should be output = {an expression with AND,OR,NOT which uses input}
(clarification: your expression can use any fixed bit-sequence or constant apart from the input)
Problem 9
The following binary numbers are 4-bit 2's complement binary numbers. Which of the following operations generate overflow? Justify your answers by translating the operands and results into decimal.
a) 0111 + 1001
b) 1000 - 0001
c) 0111 + 0001
d) 1110 + 1000
Problem 10
a)Show that the following expressions are equivalent
NOT(A OR B) = NOT(A) AND NOT(B)
(hint:write truth tables for both, and show that they have same values in all rows)
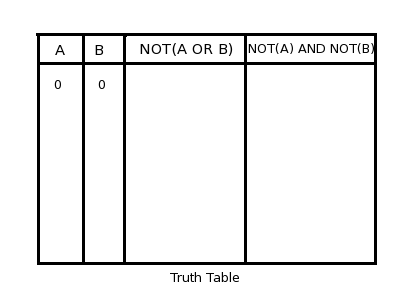
b) Using the property (a), implement the OR operation using AND and NOT operators only.
(hint: NOT(NOT(A)) = A )
|
|
 |