CS/ECE 252 Spring 2008

CS/ECE 252 Introduction to Computer Engineering
Spring 2008 All Sections
Instructor David A. Wood
TAs Spyridon Blanas, Priyananda Shenoy & Shengnan Wang
URL: http://www.cs.wisc.edu/~david/courses/cs252/Spring2008/

Homework 2 // Due at lecture Friday Feb 8

Primary contact for this homework: Priyananda Shenoy [shenoy at cs.wisc.edu]
You must submit your solutions in paper(no soft copies).
Please be sure to include your name, email address and your section.
You must do this homework alone.
Please staple multiple pages together
Helpful hint: Show all the intermediate steps for your answers. That way we can give you partial credit even if you get the answer wrong

Problem 1

a) Suppose that the total number of students in some class is 224. If each student is assigned a unique bit pattern, what is the minimum number of bits required to do this?

Let n be the minimum number of bits required, then by definition it is the smallest integer such that 2ⁿ >= 224. We can find this by trial-and-error or by taking logarithms as follows: n = ceiling( log₂ 224 ) = 8 bits.

b) Suppose that for Section 1 of this class, we need 8 bits to represent everyone uniquely. Similarly for Section 2, we need 7 bits. If both sections are combined into one big section, how many bits are required to represent everyone uniquely?

maximum number of students in section 1 = 2⁸ = 256.
maximum number of students in section 2 = 2⁷ = 128.
maximum number of students in combined section = 256 + 128 = 384.
The miminum number of bits required to represent 384 people uniquely is ceiling( log₂ 384 ) = 9 bits.

Problem 2

Interpret the following 8-bit sequence '10110010' as the following:
a) unsigned integer
1 * 2⁷ + 0 * 2⁶ + 1 * 2⁵ + 1 * 2⁴ + 0 * 2³ + 0 * 2² + 1 * 2¹ + 0 * 2⁰ = 178

b) signed magnitude integer
(-1)¹ * ( 0 * 2⁶ + 1 * 2⁵ + 1 * 2⁴ + 0 * 2³ + 0 * 2² + 1 * 2¹ + 0 * 2⁰ ) = -50

c) 1's complement integer
The most significant bit is '1' so it is a negetive number. To get its magnitute we take the complement of each bit: 01001101 and then do the same procedure as above to get the value
-1 * ( 0 * 2⁷ + 1 * 2⁶ + 0 * 2⁵ + 0 * 2⁴ + 1 * 2³ + 1 * 2² + 0 * 2¹ + 1 * 2⁰ ) = -77

d) 2's complement integer
The most significant bit is '1' so it is a negetive number. To get its magnitute we take the complement of each bit: 01001101, add 1 to it and then do the same procedure as above to get the value

	01001101
+	00000001

	01001110

The value is: -1 * ( 0 * 2⁷ + 1 * 2⁶ + 0 * 2⁵ + 0 * 2⁴ + 1 * 2³ + 1 * 2² + 1 * 2¹ + 0 * 2⁰ ) = -78

Problem 3

The range of a representation is the set of values which can be represented using that representation. For example, if an integer is represented by 5 unsigned bits, then its range is 0 to 31. What is the range of an integer represented in 8-bit 2's complement form?
-2^8-1 to +(2^8-1 - 1) = -128 to +127

Problem 4

Let X = 101010, Y = 110011 and Z = 011101. Then evaluate the following:
a) (X OR Y) AND Z

X	101010
Y	110011
X OR Y	111011
Z	011101
(X OR Y) AND Z	011001

b) X OR (Y AND Z)

Y	110011
Z	011101
Y AND Z	010001
X	101010
X OR (Y AND Z)	111011

c) (X OR Y) AND (X OR Z)

X	101010
Y	110011
X OR Y	111011
X	101010
Z	011101
X OR Z	111111
(X OR Y) AND (X OR Z)	111011

Problem 5

Convert the following bit sequence into hexadecimal
1111101011001110000011111111

starting from the left, split the number into groups of 4 bits.
1111 1010 1100 1110 0000 1111 1111
For each group of 4 bits, use the conversion table to find the hexadecimal value.
1111 = 0xF, 1010 = 0xA, 1100 = 0xC, 1110 = 0xE, 0000 = 0x0
The given value in hex is 0xFACE0FF.

(For Fun: Try making more meaningful words with hex characters. What's the longest you can make?)

Problem 6

Write the decimal equivalents for these IEEE floating point numbers.
a) 0 01010111 00000000000000000000000

The sign bit is '0', so it is a positive number. Since the exponent is greater than 0, the formula to be used is:
value = (-1)^s * 1.F * 2^E-127
Here F = 0, and the exponent E = 01010111₂ = 87₁₀
value = (-1)⁰ * 1.0 * 2^87-127 = 2^-40 = 9.095 * 10^-13

b) 1 01111010 10000000000000000000000
The sign bit is '1', so it is a negetive number. Since the exponent is greater than 0, the formula to be used is:
value = (-1)^s * 1.F * 2^E-127
Here F = 0.1₂ = 0.5₁₀, and the exponent E = 01111010₂ = 122₁₀
value = (-1)¹ * 1.5 * 2^122-127 = -3/64 = -0.046875

Problem 7

Translate the following ASCII codes into a string of characters by interpreting each group of eight bits as an ASCII character:
0x5448495320495320535041525441
(0x20 is the 'space' character)
THIS IS SPARTA
(No extra points for Leonidas jokes!)

Problem 8

Consider an operation CLEAR-EVEN-BITS which takes in an input bit sequence and gives as output the following sequence:
a) all even bits of the output(0th bit, 2nd bit etc) are set to 0
b) all odd bits of the output are the same as the corresponding input bits.
For example, if input is 11001011, then output is 10001010. See image below for clarifications

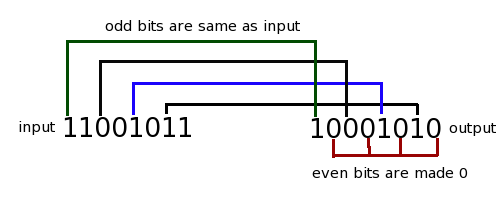
Implement this operation using any of NOT,AND,OR. Assume that the input is always 8-bits long. The 0th bit is the right most bit.
(hint:Your answer should be output = {an expression with AND,OR,NOT which uses input}
We can arrive at the answer by noticing the following properties about the AND operator:

X AND 0 = 0, irrespective of what value X takes
X AND 1 = X

You can try a few examples and convince yourself that this is true. With these properties, it is easy to implement the CLEAR-EVEN-BITS operator. We will construct a mask which, when ANDed with the input, gives us the desired output. Since we need to make the even bits '0', we can have the even bits of the mask set to 0. Since we want the odd bits to have the same value as the input, we can make these bits 1. So the complete expression is:
CLEAR-EVEN-BITS(X) = X AND 10101010

Problem 9

The following binary numbers are 4-bit 2's complement binary numbers. Which of the following operations generate overflow? Justify your answers by translating the operands and results into decimal.
a) 0111 + 1001

	0111	+7₁₀
+	1001	-7₁₀
	0000	0₁₀

No overflow

b) 1000 - 0001

	1000	-8₁₀
-	0001	+1₁₀
	0111	7₁₀

Overflow

c) 0111 + 0001

	0111	+7₁₀
+	0001	+1₁₀
	1000	-8₁₀

Overflow

d) 1110 + 1000

	1110	-2₁₀
+	1000	-8₁₀
	0110	+6₁₀

Overflow

Problem 10

a)Show that the following expressions are equivalent
NOT(A OR B) = NOT(A) AND NOT(B)
(hint:write truth tables for both, and show that they have same values in all rows)

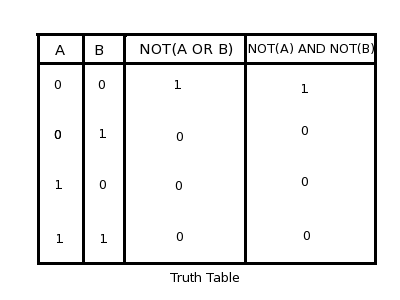
b) Using the property (a), implement the OR operation using AND and NOT operators only.
(hint: NOT(NOT(A)) = A )
A OR B = NOT( NOT(A) AND NOT(B) )

Computer Sciences | UW Home

Page last modified: Friday, 08-Feb-2008 12:19:44 CST
Feedback or content questions: send email to Email Address of David Wood
Technical or accessibility issues: lab@cs.wisc.edu
Copyright © 2002, 2003 The Board of Regents of the University of Wisconsin System.