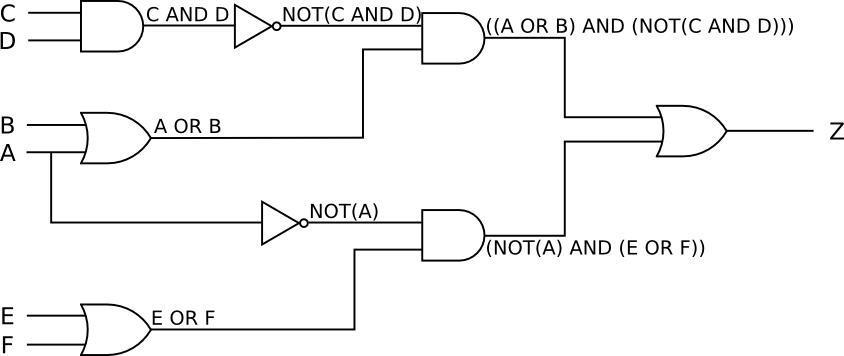
The logic circuit for this logic expression is:

The output is 1 only when more than two of the inputs are 1. Therefore, the truth table is:
|
|
A simple way to derive the logic expression from every truth table is to follow the method presented in Problem 5:
Applying this method to the truth table above gives us:
Therefore, one logic expression which is equivalent to the truth table shown above is: Z = (A AND B AND C AND D) OR (A AND B AND C AND D) OR (A AND B AND C AND D) OR (A AND B AND C AND D) OR (A AND B AND C AND D).
Notice that the solution produced by this method is correct, albeit it's more verbose than necessary. The process of coming up with an optimal solution is called minimization. A minimized expression for this problem is Z = (A AND B AND (C OR D)) OR ((A OR B) AND C AND D).
The truth table for this circuit is:
|
|
|
Z = A OR B
The truth table is:
|
|
|
|
The expression (NOT(A OR B)) is equivalent to the expression (A AND B).
DeMorgan's law.
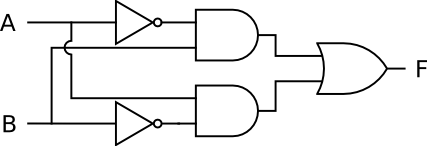
The circuit is:
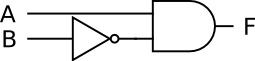
The circuit is:
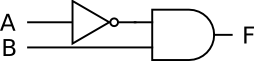
The completed circuit is:
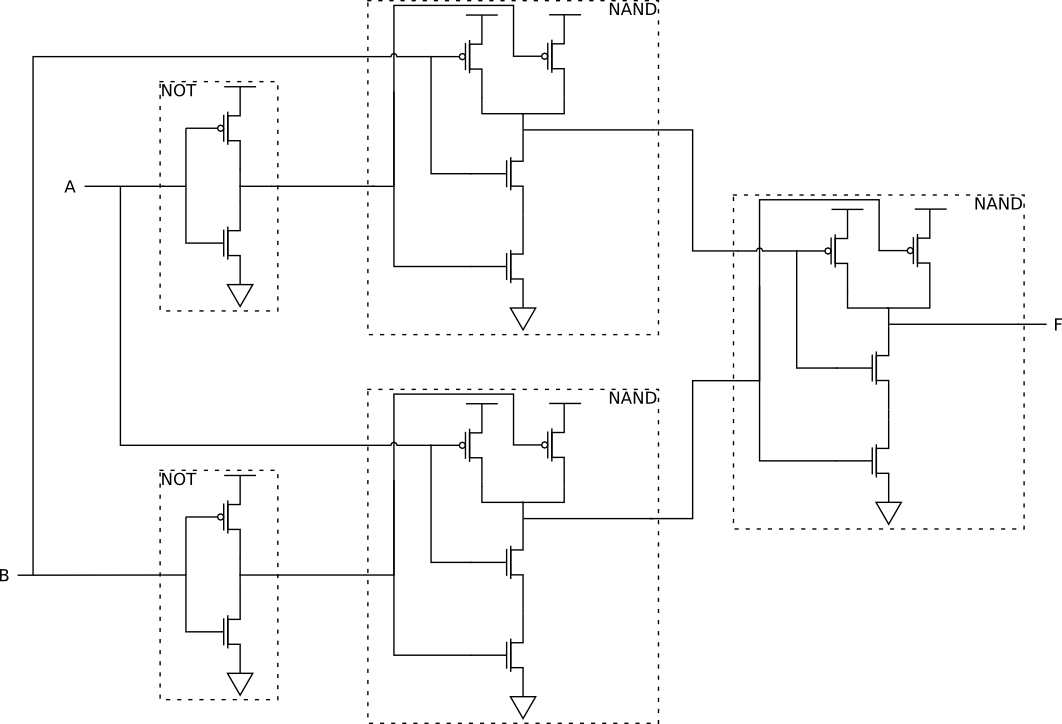
Recall that:
(A AND B) OR (C AND D) =
NOT(NOT((A AND B) OR (C AND D)) =
NOT(NOT(A AND B) AND NOT(C AND D)) =
(A NAND B) NAND (C NAND D)
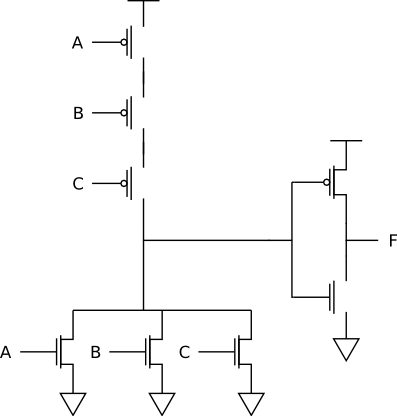
The transistor circuit is:
Recall that a b-digit binary number can store a maximum of 2b different numbers. Therefore a 14-bit adress can store 214 different memory positions. Since our memory is byte-addressable, this means that our memory consists of 214*23=214+3=217 bits. And because each nibble is 4-bits, our memory can store 217/22=217-2=215=32768 nibbles.
Notice how representing everything in powers of 2 can make the math easier. That's why all computer people love powers of 2!
Observe that:
The truth table for this circuit is:
|
|
|
The three-input AND gate is:
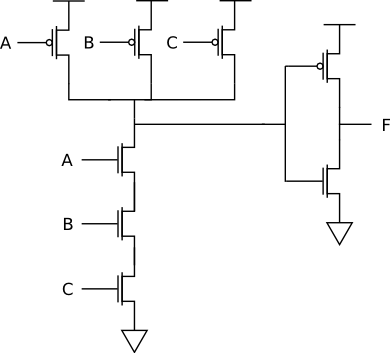
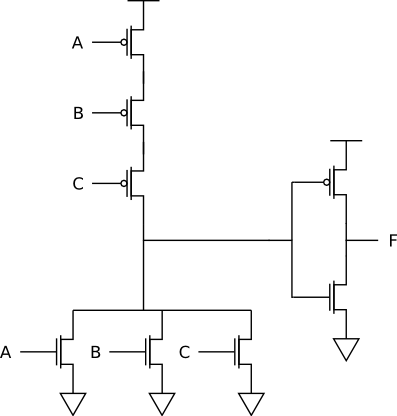
The three-input OR gate is:
For A=1, B=0, C=0, the AND gate becomes:

For A=1, B=0, C=0, the OR gate becomes:
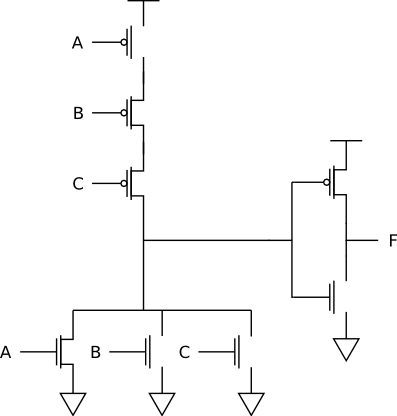
For A=0, B=0, C=0, the AND gate becomes:
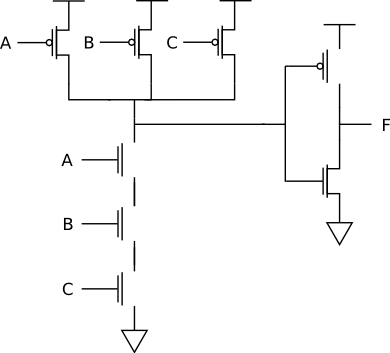
For A=0, B=0, C=0, the OR gate becomes:
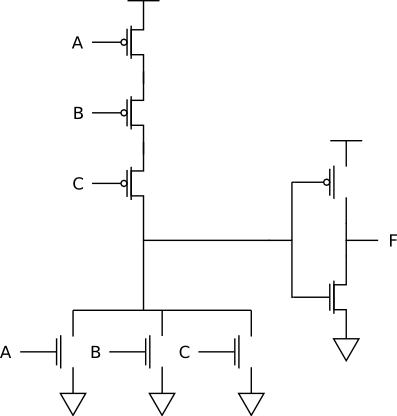
For A=1, B=1, C=1, the AND gate becomes:
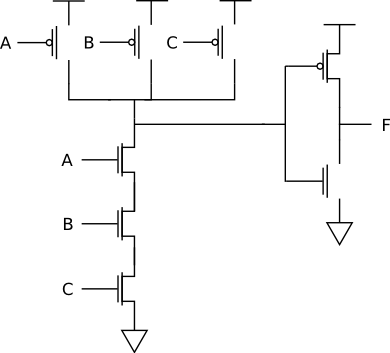
For A=1, B=1, C=1, the OR gate becomes: