University of Wisconsin - MadisonCS 540 Lecture NotesC. R. Dyer

Game Playing (Chapter 5)

Formulating Game Playing as Search

Game Trees

Searching Game Trees using the Minimax Algorithm

Steps used in picking the next move:
  1. Create start node as a MAX node (since it's my turn to move) with current board configuration
  2. Expand nodes down to some depth (i.e., ply) of lookahead in the game
  3. Apply the evaluation function at each of the leaf nodes
  4. "Back up" values for each of the non-leaf nodes until a value is computed for the root node. At MIN nodes, the backed up value is the minimum of the values associated with its children. At MAX nodes, the backed up value is the maximum of the values associated with its children.
  5. Pick the operator associated with the child node whose backed up value determined the value at the root

Note: The above process of "backing up" values gives the optimal strategy that BOTH players would follow given that they both have the information computed at the leaf nodes by the evaluation function. This is implicitly assuming that your opponent is using the same static evaluation function you are, and that they are applying it at the same set of nodes in the search tree.

Minimax Algorithm in Java

public int minimax(s)
{
  int [] v = new int[#ofSuccessors];
  if (leaf(s))
       return(static-evaluation(s));
  else 
  {
    // s1, s2, ..., sk are the successors of s
    for (int i = 1; i < #ofSuccessors; i++)
    {
      v[i] = minimax(si);
    }
    if (node-type(s) = max)
      return max(v1, ..., vk);
      else return min(v1, ..., vk);
   }
}

Example of Minimax Algorithm

    For example, in a 2-ply            MAX ......  S
    search, the MAX player                       / | \ 
    considers all (3) possible                 /   |   \
    moves.                           MIN .... A    B    C
                                             /|\   |\   |\
    The opponent MIN also                   / | \  | \  | \
    considers all possible                 D  E  F G  H I  J
    moves.  The evaluation function      100  3 -1 6  5 2  9
    is applied to the leaf level only.

Once the static evaluation function is applied at the leaf nodes, backing up values can begin. First we compute the backed-up values at the parents of the leaves. Node A is a MIN node corresponding to the fact that it is a position where it's the opponent's turn to move. A's backed-up value is -1 (= min(100, 3, -1), meaning that if the opponent ever reaches the board associated with this node, then it will pick the move associated with the arc from A to F. Similarly, B's backed-up value is 5 (corresponding to child H) and C's backed-up value is 2 (corresponding to child I).

Next, we backup values to the next higher level, in this case to the MAX node S. Since it is our turn to move at this node, we select the move that looks best based on the backed-up values at each of S's children. In this case the best child is B since B's backed-up value is 5 (= max(-1, 5, 2)). So the minimax value for the root node S is 5, and the move selected based on this 2-ply search is the move associated with the arc from S to B.

It is important to notice that the backed-up values are used at nodes A, B, and C to evaluate which is best for S; we do not apply the static evaluation function at any non-leaf node. Why? Because it is assumed that the values computed at nodes farther ahead in the game (and therefore lower in the tree) are more accurate evaluations of quality and therefore are preferred over the evaluation function values if applied at the higher levels of the tree.

Notice that, in general, the backed-up value of a node changes as we search more plies. For example, A's backed-up value is -1. But if we had searched one more ply, D, E and F will have their own backed-up values, which are almost certainly going to be different from 100, 3 and -1, respectively. And, in turn, A will likely not have -1 as its backed-up value. We are implicitly assuming that the deeper we search, the better the quality of the final outcome.

Alpha-Beta Pruning

Alpha-Beta Algorithm

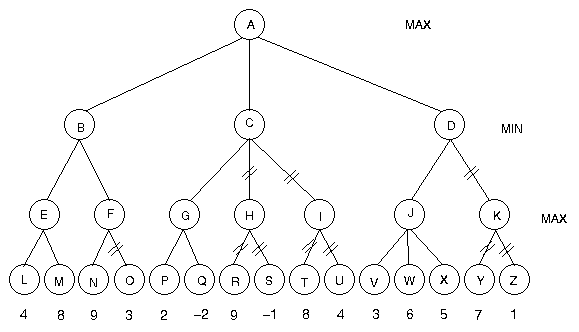
Example of Alpha-Beta Algorithm on a 3-Ply Search Tree

Below is a search tree where a beta cutoff occurs at node F and alpha cutoffs occur at nodes C and D. In this case we've pruned 10 nodes (O,H,R,S,I,T,U,K,Y,Z) from the 26 that are generated by Minimax.

Effectiveness of Alpha-Beta

Cutting off Search (or, when to stop and apply the evaluation function)

So far we have assumed a fixed depth d where the search is stopped and the static evaluation function is applied. But there are variations on this that are important to note:

Copyright © 1996-2003 by Charles R. Dyer. All rights reserved.