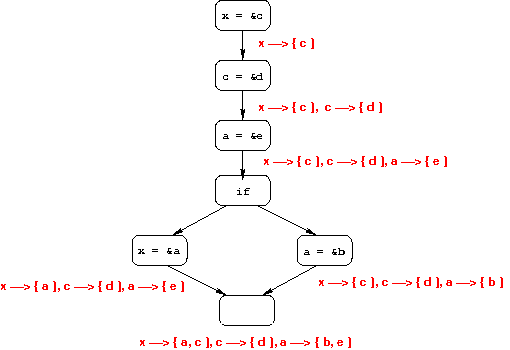
Das's Analysis
Das's algorithm is based on the observation (made by doing studies of
C programs) that in C code, most pointers arise because the address of
a variable is passed as a parameter.
This is done either to simulate call-by-reference (i.e., so that the procedure can modify that parameter), or for efficiency (e.g., when the parameter is a struct or an array).
This observation is important because the use of pointer parameters
can cause Steensgaard's algorithm to lose precision when a pointer
parameter is passed on from one procedure to another, or when two different
procedures are called with the same pointer parameter.
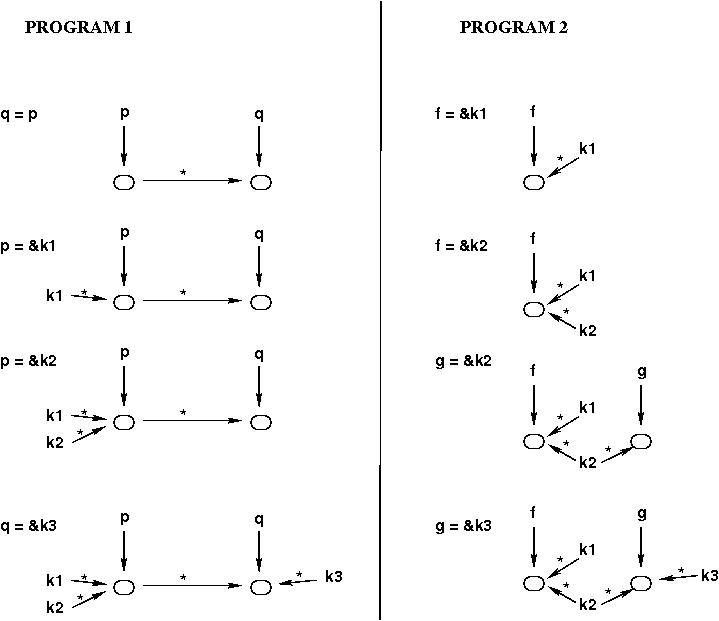
For example, consider the two programs shown below.
For each program, the actual code is shown on the left, and
the equivalent set of assignment statements is shown on the right.
void Q(int *q) { |
*q = ...; |
} |
|
void P(int *p) { |
Q(p); | q = p
} |
|
int main() { |
int k1, k2, k3; |
P(&k1); | p = &k1
P(&k2); | p = &k2
Q(&k3); | q = &k3
} |
_________________________________________________
PROGRAM 2
void F(int *f) { |
... |
} |
|
void G(int *g) { |
... |
} |
|
int main() { |
int k1, k2, k3; |
F(&k1); | f = &k1
F(&k2); | f = &k2
G(&k2); | g = &k2
G(&k3); | g = &k3
} |
Here are the points-to graphs that would be built using
Andersen's analysis and using
Steensgaard's analysis:
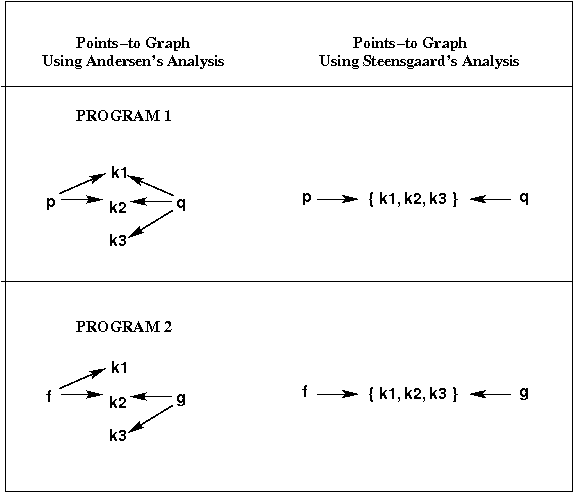
The loss of precision for Program 1 (the inclusion of the "extra" fact
p → k3), occurs when processing the assignment
q = p.
The way Steensgaard handles a "copy assignment" like that
is to merge the points-to sets of the left- and right-hand side
variables;
i.e., to treat the assignment as symmetric.
Das handles q = p differently:
instead of merging points-to sets, he introduces what he calls
a flow edge into the points-to graph from the node
that represents p's points-to set to the node that
represents q's points-to set.
(If those nodes don't exist, empty dummy nodes are added.)
This flow edge means that all
of the addresses in the points-to set of p
are also in the set of q.
In fact, flow edges are introduced when processing all
assignment statements,
including ones of the form v1 = &v2.
As in Steensgaard's algorithm, each node in the points-to graph
has only a single outgoing "points-to" edge, but it can have
any number of outgoing flow edges.
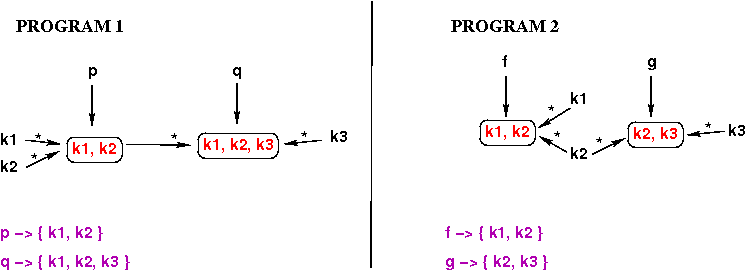
Below are the sequences of assignments for example Programs 1 and 2
again, and the corresponding sequences of points-to graphs built by
Das's algorithm.
The points-to graphs shown are actually slightly simplified;
we will see the missing parts below.
In the graphs, points-to edges are shown as plain arrows, and
flow edges are shown as arrows with stars above them.
Like Steensgaard, Das processes each assignment in the program
just once, building a points-to graph with both points-to and
flow edges.
After the graph is built, sets of variables must be propagated
forward along the flow edges to form the final points-to sets.
The results of this propagation step for the two final
points-to graphs shown above are shown below, along with the
final points-to sets for each variable.
The simplification in the above points-to graphs has to do with the
fact that
Das's algorithm is similar to Steensgaard's in that it does
merge some points-to sets.
In particular, whenever a flow edge n1 *→ n2
is added, all points-to sets "below" n1 and n2
are merged.
In order for this to work, whenever a flow
edge n1 *→ n2 is added to the graph,
outgoing points-to edges (to dummy nodes)
are also added if they don't already exist.
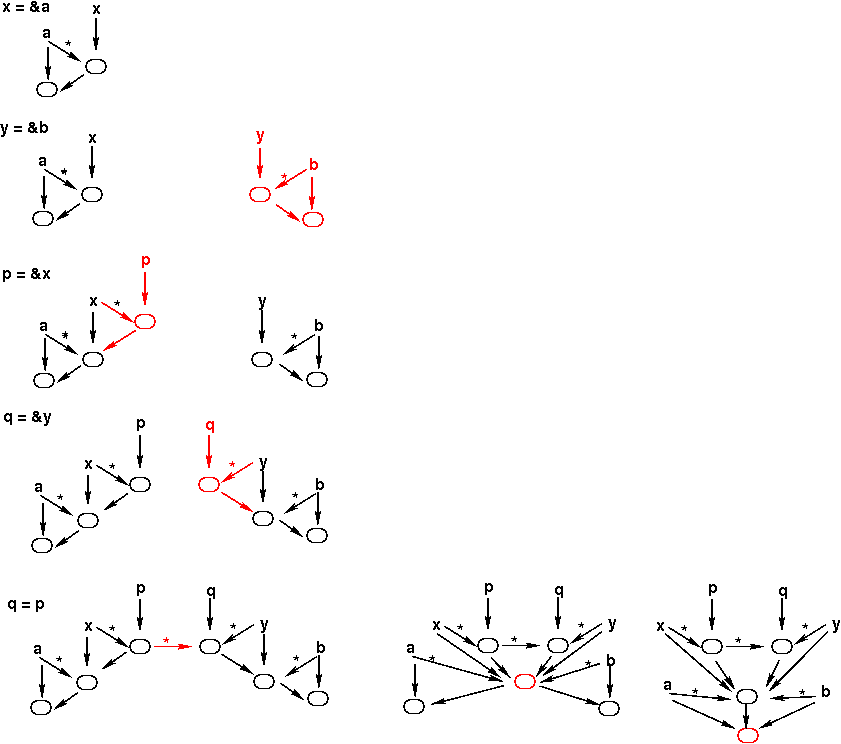
Below is an example that illustrates that, as well as illustrating
the merging of points-to sets performed by Das's algorithm.
The merging occurs after the last assignment (q = p).
In the figure below, this is illustrated using three points-to
graphs to illustrate (left-to-right)
- adding the flow edge that puts everything in p's
points-to set into q's points-to set;
- merging the points-to sets below those of p and q;
- merging the points-to successors of the nodes that were just
merged.
In each points-to graph, the new nodes and edges are shown in red.
It is worth noting that because Das's algorithm only merges nodes
below a flow edge, it maintains precision for "top-level"
pointers;
i.e., pointers that are not themselves pointed to.