Interprocedural Analysis: Motivation and Overview

Motivation
Approach 1 (use safe dataflow functions)
Approach 2 (use the supergraph)
Approach 3 (use summary information)
Approach 4 (use summary functions)
- Callahan et al
- Sharir and Pnueli

Motivation

We need information about the effects of a procedure to propagate dataflow information across a call. For example:

    x=0;  
	// is y live here? (yes iff used in procedure P)
    call P();
	// is x still equal to 0 here? (yes iff not changed in P)
    y=x;

Note: sometimes this is not an issue, for example when we are tracking information only for non-aliased locals, and using call-by-value only.

We also need information about call sites to start dataflow analysis for procedures other than "main". For example:

    procedure P(int a, int b)
    { // what are the values of a, b, and globals here?
      .
      .
      .
      // what globals are live here?
      // if a and b are passed by reference, are they live here?
     }

The answers to these questions depend on what is true before/after the calls to procedure P (before for forward problems, and after for backward problems).

Note that pointers and reference parameters make it especially difficult to answer these kinds of questions. For example:

procedure P(ref x, ref y) {
    x = 0;
    y = 1;
            // is x==0 here? yes iff x,y not aliases
    g = 0;
            // is y==1 here? yes iff y,g not aliases
    *p = 1;
            // is g==0 here? yes iff p does not point to g
}

Reference parameters are actually implemented using pointers, so any solution that handles pointers can handle reference parameters, too. (One solution is to assume that a pointer can point to ANY memory location; another is to assume that it can point to any heap-allocated location, or to any stack location whose address is taken somewhere in the program. Pointer analysis can be used to narrow the possibilities further.) There are some approaches that handle reference parameters but not pointers in general. We will look at one such approach later; for now, we'll assume that the programs we deal with contain no pointers or reference parameters.

There are several possible approaches to handling programs with procedure calls; some address what to do for procedure entry/exit; some address what to do for a procedure call; some address both issues.

Approach 1 (use safe dataflow functions)

A simple way to deal with procedure calls is to do no special analysis, and to use safe dataflow functions for the entry/exit node of each procedure (the entry node for a forward problem, the exit node for a backward problem), and for every call node.

For example:

1. Dataflow functions for entry/exit nodes:

Reaching Defs: the function for the enter node returns the set (x, enter) for all globals and formal parameters x (i.e., we consider there to be an implicit assignment to all globals and formals at the entry node).
Constant Propagation: the function for the enter node returns the empty set (i.e., no variables are considered to be constant at the start of the procedure).
Live Variables: the function for the exit node returns the set of all global variables (i.e., all globals are considered to be live after this procedure returns).

2. Dataflow functions for call node n:

Reaching Defs: f_n(S) = S U {(g,n) | g is a global}; i.e., we consider every call to be a potential definition of every global (note that since the call may not define a global, the dataflow function does not remove anything from the reaching-definitions set).
Constant Propagation: f_n(S) = S - (g, *), where g is a global (i.e., we consider every procedure call as setting every global to a non-constant value).
Live Variables: f_n(S) = S U {x | x is a global or an actual in this call}; i.e., we consider every global live before every call, and we assume that every actual may be used in the called procedure before being overwritten.

Approach 2 (use the supergraph)

Another approach that requires no additional analysis involves converting the entire program to a single CFG (called a supergraph) by first building the CFGs for the individual procedures, then adding edges as follows for each procedure P:

from "call P" to enter P
from "exit P" to all nodes following "call P"

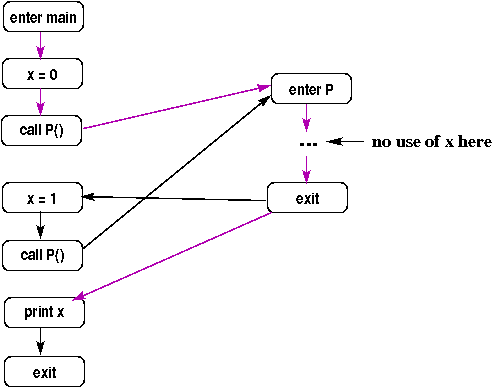
We can now do normal dataflow analysis on this supergraph. For a forward problem, we would start at the enter node of "main"; for a backward problem, we would start at main's exit node.

A problem with this approach is that it includes interprocedurally invalid paths: paths that correspond to a procedure being called from one call site but returning to another. This is bad because the results of the analysis will generally be less accurate (i.e., more conservative) than if the paths were restricted to include only interprocedurally valid paths (paths that go from a call site to the called procedure and back to the same call site). For example, the following shows a supergraph with an invalid path shown using dashed purple edges (representing the first call to p returning to the second call site).

If we do normal constant propagation on this supergraph, we will take this invalid path into account, and thus will conclude that g is not constant at either print statement (while in fact g is 0 at the first print statement, and 1 at the second print statement).

Approach 3 ((use summary information)

An approach that does require additional analysis (before doing our usual dataflow analysis on the CFGs for each procedure) involves using summary information about each procedure to determine a safe (conservative) dataflow function for every call node. Typically, summary information tells what variables might be modified and might be used by each procedure. Since we are assuming no reference parameters, this means the set of globals that might be modified, and the set of globals and formals that might be used.

Example

Assume we know that procedure P may modify globals x and y, and may use globals y and z. Below are the dataflow functions we would use for node n, a call to P, for several dataflow problems.

Dataflow Problem Dataflow Function for Call Node n

reaching definitions f_n(S) = S U {(x,n),(y,n)}

live variables f_n(S) = S U {y,z}

constant propagation f_n(S) = S - ((x, *), (y, *))

Notes:

For reaching definitions, we cannot assume that the procedure call kills anything (because all we know is that procedure P may modify x and y). Similarly, for live variables, we cannot assume that the call "kills" any variables.
If we know that P might use its first formal parameter, and the call at node n is: P(a, b), then the dataflow function for live variables must also add "a" to the given set.

Note that this approach only addresses the question of how to handle a call node; it doesn't help with the problem of determining what dataflow facts hold at the start/end of a procedure.

Approach 4 (use summary functions)

This approach is more ambitious than approach 3, and can be used to define dataflow functions for the enter/exit nodes of the procedures in a program as well as the dataflow functions for the call nodes. In what follows, we assume that we're dealing with a forward dataflow-analysis problem (handling backward problems is similar).

We will consider the work of two different research groups: Callahan et al, and Sharir and Pnueli.

Callahan et al

This work is described in one of our on-line readings:

Interprocedural constant propagation

This paper discusses constant propagation only (though the ideas can be used for other dataflow-analysis problems). They assume that parameters are passed by reference, they ignore globals, and they assume that alias analysis has been done (i.e., for each assignment to a formal x, and for each use of formal x, you know what other formals might be assigned-to or used because it is aliased to x).

The paper describes how to compute a summary function for each call node or for each procedure (they do not discuss how to combine the two ideas). The summary function for a call node in procedure Q summarizes the effect of all paths in Q from Q's enter node to the call on the values of the actuals used at the call. Given summary functions for all call nodes that represent calls to P, we can figure out which of P's formals is guaranteed to be constant at the start of P.

The summary function for a procedure P summarizes the effect of all paths from P's enter node to its exit node on the values of its formals (remember that we're assuming that all parameters are passed by reference); i.e., it summarizes the effect of a call to P on the actuals used at that call, and thus can be used to define the dataflow function for a call node that represents a call to P.

Example:

void main() {
s1:  call P1(10, 20);
s2:  call P1(10, 30);
}

void P1(int a, int b) {
s3:  call P2(a, b);
     print(a);
     print(b);
}

void P2(int x, int y) {
  y = x;
}

For constant propagation, the summary function for the first call (labeled s1) would say that the first actual is 10, and the second actual is 20. The summary function for the second call (labeled s2) would say that the first actual is 10, and the second actual is 30. The summary function for the third call (labeled s3) would say that the first actual has the same value as the formal a, and the second actual has the same value as the formal b.

Combining the summary functions for the two calls to P1, we would find that P1's formal a always has the value 10 (at the start of P1), while its formal b does not have a constant value. Once we have that information, we can conclude that P2's formal x always has the value 10 (at the start of P2), while y is not constant.

If we use the same example to consider summary functions for the three procedures, we see that P2 does not change its formal x (i.e., x's value at the end of P2 is the same as its initial value), while the final value of y is the same as the initial value of x. That allows us to define the dataflow function for the call to P2 (at s3) as essentially:

b = a;

Sharir and Pnueli

The techniques of Sharir and Pnueli work only for dataflow problems for which we can compute meets and compositions of dataflow functions, and for which we can compare two dataflow functions for equality (in practice, this means that we need to have a canonical representation of the dataflow functions; e.g., a GEN and a KILL set).

Sharir and Pnueli assume that we're dealing only with globals (no locals, no parameters), and thus there is no issue of aliasing. Their techniques are more general than those of Callahan et al. The idea is to compute, for every CFG node n, a "phi function" Φ_enter,n that summarizes the effects of all paths from the enter node to node n (where the input to the phi function is the dataflow fact that holds at the enter node). Note that computing the phi functions requires iteration for a program with either recursion of loops (since the definitions of two phi functions can be mutually dependent).

Once all of the phi functions have been computed, they can be used to compute the dataflow facts that hold at each node. Iteration is needed again for recursive programs, because in that case the dataflow facts for call and enter nodes can be mutually dependent.

Return to Interprocedural Analysis table of contents.

Go to the next section.

Dataflow Problem	Dataflow Function for Call Node n
reaching definitions	f_n(S) = S U {(x,n),(y,n)}
live variables	f_n(S) = S U {y,z}
constant propagation	f_n(S) = S - ((x, ), (y, ))