Homework 2 Solution

Question 1

Part a

expr → expr OR term 
     | term
term → term item 
     | item
item → item STAR 
     | item PLUS 
     | LTR 
     | EPS 
     | LPAR expr RPAR

Note: the solution is not unique.

Part b

Question 2

CFG 1:

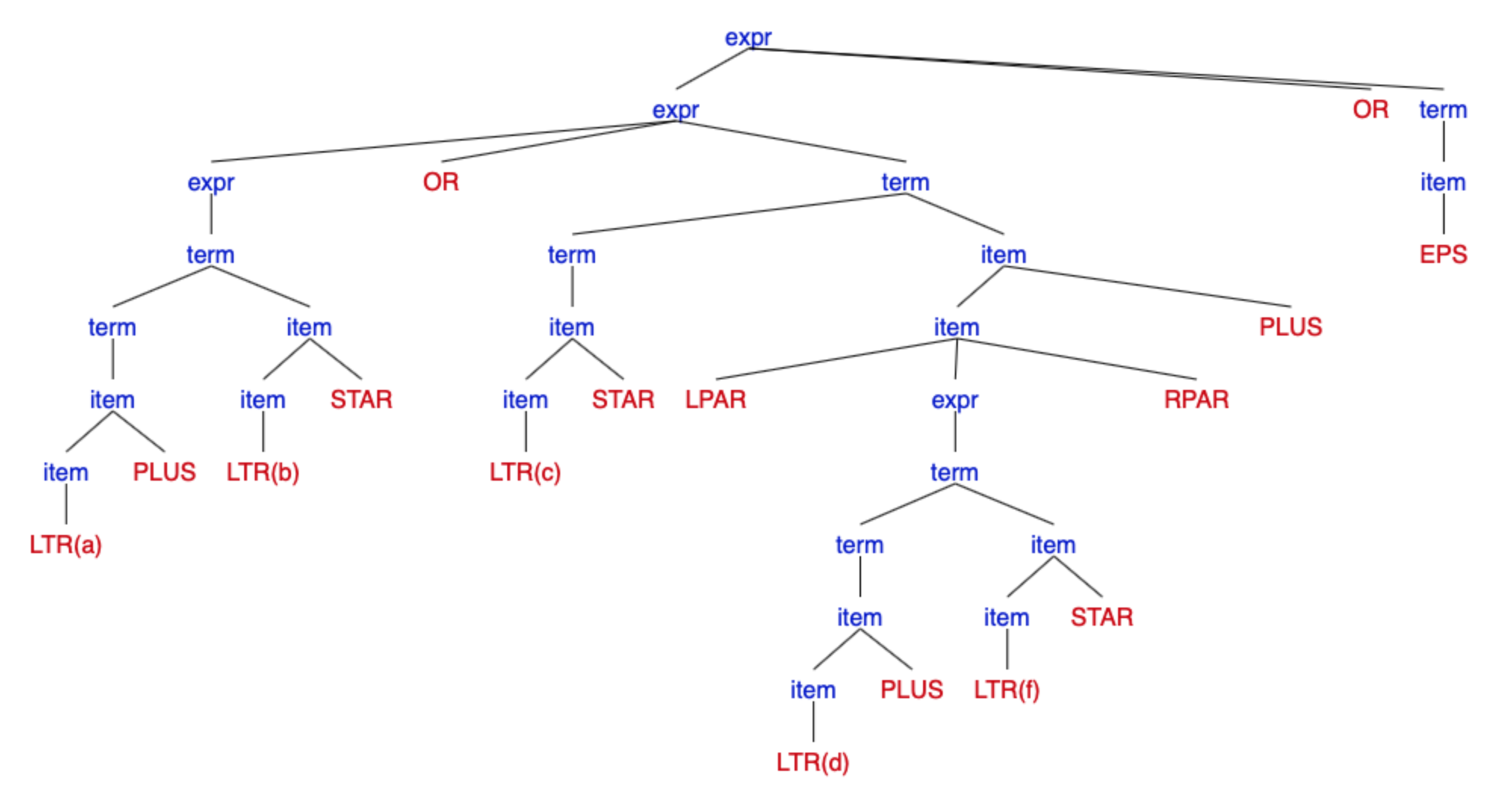
This CFG doesn't allow empty list. Here is a string that is a legal set expression but is not in the language of the CFG:

{ }

CFG 2:

This CFG is ambiguous. Below are two different parse trees for the string { }. Different parse trees can also be built for expressions with operators so that one tree groups the subexpressions correctly (according to the precedence and associativeity rules) and the other does not.

   exp               exp
  /   \               |
 {     }             term
                      |
                    factor
                      |
                     set
                      |
                     exp
                    /   \
                   {     }

This CFG also allows a list of names to start with a comma. Here is a string that is not a legal set expression but is in the language of the CFG:

{ , NAME }

CFG 3:

This CFG doesn't allow parentheses around the right-hand operand of a union or intersection. Here is a legal set expression that is not in the language of the CFG:

{ } ∪ ( { } )

CFG 4:

This CFG doesn't allow two or more unions in a row. Here is a legal set expression that is not in the language of the CFG:

{ } ∪ { } ∪ { }

It also doesn't allow a union to the right of an intersection. Here is another legal set expression that is not in the language of the CFG:

{ } ∩ { } ∪ { }

CFG 5:

This CFG is correct.

Question 3

Part a

Grammar rule	Translation rule
`program → MAIN LPAREN RPAREN LCURLY list RCURLY`	`program.trans = list.trans`
`list → list oneItem`	`list₁.trans = list₂.trans ∪ oneItem.trans`
`list → epsilon`	`list.trans = { }`
`oneItem → decl`	`oneItem.trans = { }`
`oneItem → stmt`	`oneItem.trans = stmt.trans`
`decl → BOOL ID SEMICOLON`	no translation rule needed
`decl → INT ID SEMICOLON`	no translation rule needed
`stmt → ID ASSIGN exp SEMICOLON`	`stmt.trans = { ID.value } ∪ exp.trans`
`stmt → IF LPAREN exp RPAREN stmt`	`stmt₁.trans = exp.trans ∪ stmt₂.trans`
`stmt → LCURLY list RCURLY`	`stmt.trans = list.trans`
`exp → exp PLUS exp`	`exp₁.trans = exp₂.trans ∪ exp₃.trans`
`exp → exp LESS exp`	`exp₁.trans = exp₂.trans ∪ exp₃.trans`
`exp → exp EQUALS exp`	`exp₁.trans = exp₂.trans ∪ exp₃.trans`
`exp → ID`	`exp.trans = { ID.value }`
`exp → BOOLLITERAL`	`exp.trans = { }`
`exp → INTLITERAL`	`exp.trans = { }`