
Recall that the parser must produce output (e.g., an abstract-syntax tree) for the next phase of the compiler. This involves doing a syntax-directed translation -- translating from a sequence of tokens to some other form, based on the underlying syntax.
A syntax-directed translation is defined by augmenting the CFG: a translation rule is defined for each production. A translation rule defines the translation of the left-hand side nonterminal as a function of:
Below is the definition of a syntax-directed translation that translates an arithmetic expression to its integer value. When a nonterminal occurs more than once in a grammar rule, the corresponding translation rule uses subscripts to identify a particular instance of that nonterminal. For example, the rule exp $\rightarrow$ exp PLUS term has two exp nonterminals; exp1 means the left-hand-side exp, and exp2 means the right-hand-side exp. Also, the notation xxx.value is used to mean the value associated with token xxx.
| CFG Production | Translation rules | |||
| exp | $\longrightarrow$ | exp PLUS term | exp1.trans = exp2.trans + term.trans | |
| exp | $\longrightarrow$ | term | exp.trans = term.trans | |
| term | $\longrightarrow$ | term TIMES factor | term1.trans = term2.trans * factor.trans | |
| term | $\longrightarrow$ | factor | term.trans = factor.trans | |
| factor | $\longrightarrow$ | INTLITERAL | factor.trans = INTLITERAL.value | |
| factor | $\longrightarrow$ | LPARENS exp RPARENS | factor.trans = exp.trans | |
consider evaluating these rules on the input 2 * (4 + 5). The result is the following annotated parse tree:

Consider a language of expressions that use the three operators: +, &&, == using the terminal symbols PLUS, AND , EQUALS, respectively. Integer literals are represented by the same INTLITERAL token we've used before, and TRUE and FALSE represent the literals true and false (note that we could have just as well defined a single BOOLLITERAL token that the scanner would populate with either true or false).
Let's define a syntax-directed translation that type checks these expressions; i.e., for type-correct expressions, the translation will be the type of the expression (either int or bool), and for expressions that involve type errors, the translation will be the special value error. We'll use the following type rules:
| CFG Production | Translation rules | |||
| exp | $\longrightarrow$ | exp PLUS term | if (exp2.trans == int and (term.trans == int) then
exp1.trans = int else exp1.trans = error |
|
| exp | $\longrightarrow$ | exp AND term | if (exp2.trans == bool and (term.trans == bool) then
exp1.trans = bool else exp1.trans = error |
|
| exp | $\longrightarrow$ | exp EQUALS term | if (exp2.trans == term.trans) and (term.trans $\neq$ error) then
exp1.trans = bool else exp1.trans = error |
|
| exp | $\longrightarrow$ | term | exp.trans = term.trans | |
| term | $\longrightarrow$ | TRUE | term.trans = bool | |
| term | $\longrightarrow$ | FALSE | term.trans = bool | |
| term | $\longrightarrow$ | INTLITERAL | term.trans = int | |
| term | $\longrightarrow$ | LPARENS exp RPARENS
|
| term.trans = exp.trans
|
|
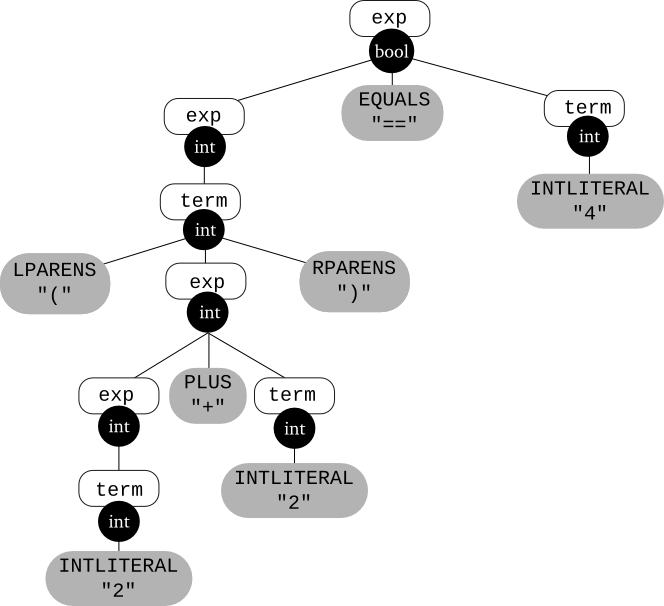
Here's an annotated parse tree for the input (2 + 2) == 4
The following grammar defines the language of base-2 numbers:
B -> 0 -> 1 -> B 0 -> B 1Define a syntax-directed translation so that the translation of a binary number is its base 10 value. Illustrate your translation scheme by drawing the parse tree for 1001 and annotating each nonterminal in the tree with its translation.
Building an Abstract-Syntax Tree
So far, our example syntax-directed translations have produced simple values (an int or a type) as the translation of an input. In practice however, we want the parser to build an abstract-syntax tree as the translation of an input program. But that is not really so different from what we've seen so far; we just need to use tree-building operations in the translation rules instead of, e.g., arithmetic operations.
First, let's consider how an abstract-syntax tree (AST) differs from a parse tree. An AST can be thought of as a condensed form of the parse tree:
Below is an example of the parse tree and the AST for the expression 3 * (4 + 2) (using the usual arithmetic-expression grammar that reflects the precedences and associativities of the operators). Note that the parentheses are not needed in the AST because the structure of the AST defines how the subexpressions are grouped.

For constructs other than expressions, the compiler writer has some choices when defining the AST -- but remember that lists (e.g., lists of declarations lists of statements, lists of parameters) should be flattened, that operators (e.g., "assign", "while", "if") go at internal nodes, not at leaves, and that syntactic details are omitted.
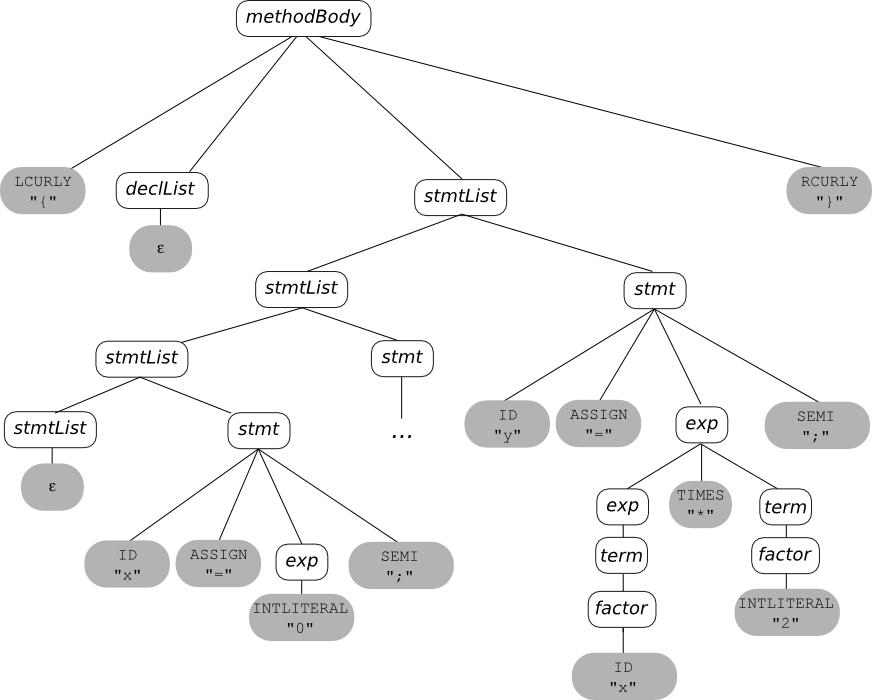
Input
=====
{
x = 0;
while (x<10) {
x = x+1;
}
y = x*2;
}
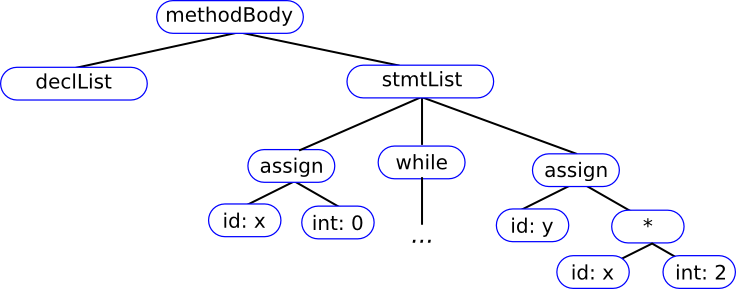
Parse Tree:
Translation Rules That Build an AST
To define a syntax-directed translation so that the translation of an input is the corresponding AST, we first need operations that create AST nodes. Let's use java code, and assume that we have the following class hierarchy:
class ExpNode { }
class IntLitNode extends ExpNode {
public IntLitNode(int val) {...}
}
class PlusNode extends ExpNode {
public PlusNode( ExpNode e1, ExpNode e2 ) { ... }
}
class TimesNode extends ExpNode {
public TimesNode( ExpNode e1, ExpNode e2 ) { ... }
}
Now we can define a syntax-directed translation for simple arithmetic expressions,
so that the translation of an expression is its AST:
| CFG Production | Translation rules | |||
| exp | $\longrightarrow$ | exp PLUS term | exp1.trans = new PlusNode(exp2, term.trans) | |
| exp | $\longrightarrow$ | term | exp.trans = term.trans | |
| term | $\longrightarrow$ | term TIMES factor | term1.trans = new TimesNode(term2.trans, factor.trans) | |
| term | $\longrightarrow$ | factor | term.trans = factor.trans | |
| factor | $\longrightarrow$ | INTLITERAL | factor.trans = new IntLitNode(INTLITERAL.value) | |
| factor | $\longrightarrow$ | LPARENS exp RPARENS | factor.trans = exp.trans | |
Illustrate the syntax-directed translation defined above by drawing the parse tree for the expression 2 + 3 * 4, and annotating the parse tree with its translation (i.e., each nonterminal in the tree will have a pointer to the AST node that is the root of the subtree of the AST that is the nonterminal's translation).