- MOP Solution
- Solving a set of equations
- Iterative algorithms
- The Lattice Model of DataflowAnalysis
- Summary
Motivation for Dataflow Analysis
A compiler can perform some optimizations based only on local information. For example, consider the following code:
x = a + b; x = 5 * 2;It is easy for an optimizer to recognize that:
- The first assignment to x is a "useless" assignment, since the value computed for x is never used (and thus the first statement can be eliminated from the program).
- The expression 5 * 2 can be computed at compile time, simplifying the second assignment statement to x = 10;
Some optimizations, however, require more "global" information. For example, consider the following code:
a = 1; b = 2; c = 3; if (...) x = a + 5; else x = b + 4; c = x + 1;In this example, the initial assignment to c (at line 3) is useless, and the expression x + 1 can be simplified to 7, but it is less obvious how a compiler can discover these facts since they cannot be discovered by looking only at one or two consecutive statements. A more global analysis is needed so that the compiler knows at each point in the program:
- which variables are guaranteed to have constant values, and
- which variables will be used before being redefined.
Examples of constant propagation and live-variable analysis
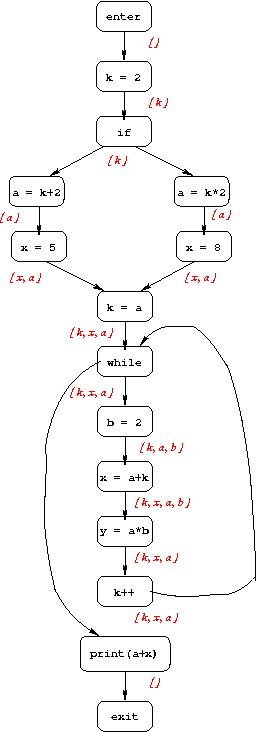
Below are examples illustrating two dataflow-analysis problems: constant propagation and live-variable analysis. Both examples use the following program:
1. k = 2;
2. if (...) {
3. a = k + 2;
4. x = 5;
5. } else {
6. a = k * 2;
7. x = 8;
8. }
9. k = a;
10. while (...) {
11. b = 2;
12. x = a + k;
13. y = a * b;
14. k++;
15. }
16. print(a+x);
Constant Propagation
The goal of constant propagation is to determine where in the program variables are guaranteed to have constant values. More specifically, the information computed for each CFG node n is a set of pairs, each of the form (variable, value). If we have the pair (x, v) at node n, that means that x is guaranteed to have value v whenever n is reached during program execution.
Below is the CFG for the example program, annotated with constant-propagation information.

Live-Variable Analysis
The goal of live-variable analysis is to determine which variables are "live" at each point in the program; a variable is live if its current value might be used before being overwritten. The information computed for each CFG node is the set of variables that are live immediately after that node. Below is the CFG for the example program, annotated with live variable information.
Draw the CFG for the following program, and annotate it with the constant-propagation and live-variable information that holds before each node.
N = 10;
k = 1;
prod = 1;
MAX = 9999;
while (k <= N) {
read(num);
if (MAX/num < prod) {
print("cannot compute prod");
break;
}
prod = prod * num;
k++;
}
print(prod);
Defining a Dataflow Problem
Before thinking about how to define a dataflow problem, note that there are two kinds of problems:
- Forward problems (like constant propagation) where the information at a node n summarizes what can happen on paths from "enter" to n.
- Backward problems (like live-variable analysis), where the information at a node n summarizes what can happen on paths from n to "exit".
Another way that many common dataflow problems can be categorized is as may problems or must problems. The solution to a "may" problem provides information about what may be true at each program point (e.g., for live-variables analysis, a variable is considered live after node n if its value may be used before being overwritten, while for constant propagation, the pair (x, v) holds before node n if x must have the value v at that point).
Now let's think about how to define a dataflow problem so that it's clear what the (best) solution should be. When we do dataflow analysis "by hand", we look at the CFG and think about:
- What information holds at the start of the program.
- When a node n has more than one incoming edge in the CFG, how to combine the incoming information (i.e., given the information that holds after each predecessor of n, how to combine that information to determine what holds before n).
- How the execution of each node changes the information.
This intuition leads to the following definition. An instance of a dataflow problem includes:
- a CFG,
- a domain D of "dataflow facts",
- a dataflow fact "init" (the information true at the start of the program for forward problems, or at the end of the program for backward problems),
- an operator ⌈⌉ (used to combine incoming information from multiple predecessors),
- for each CFG node n, a dataflow function fn : D → D (that defines the effect of executing n).
For constant propagation, an individual dataflow fact is a set of pairs of the form (var, val), so the domain of dataflow facts is the set of all such sets of pairs (the power set). For live-variable analysis, it is the power set of the set of variables in the program.
For both constant propagation and live-variable analysis, the "init" fact is the empty set (no variable starts with a constant value, and no variables are live at the end of the program).
For constant propagation, the combining operation ⌈⌉ is set intersection. This is because if a node n has two predecessors, p1 and p2, then variable x has value v before node n iff it has value v after both p1 and p2. For live-variable analysis, ⌈⌉ is set union: if a node n has two successors, s1 and s2, then the value of x after n may be used before being overwritten iff that holds either before s1 or before s2. In general, for "may" dataflow problems, ⌈⌉ will be some union-like operator, while it will be an intersection-like operator for "must" problems.
For constant propagation, the dataflow function associated with a CFG node that does not assign to any variable (e.g., a predicate) is the identity function. For a node n that assigns to a variable x, there are two possibilities:
- The right-hand side has a variable that is not constant. In this case, the function result is the same as its input except that if variable x was constant the before n, it is not constant after n.
- All right-hand-side variables have constant values. In this case, the right-hand side of the assignment is evaluated producing consant-value c, and the dataflow-function result is the same as its input except that it includes the pair (x, c) for variable x (and excludes the pair for x, if any, that was in the input).
For live-variable analysis, the dataflow function for each node n has the form: fn(S) = (S - KILLn) union GENn, where KILLn is the set of variables defined at node n, and GENn is the set of variables used at node n. In other words, for a node that does not assign to any variable, the variables that are live before n are those that are live after n plus those that are used at n; for a node that assigns to variable x, the variables that are live before n are those that are live after n except x, plus those that are used at n (including x if it is used at n as well as being defined there).
An equivalent way of formulating the dataflow functions for live-variable analysis is: fn(S) = (S intersect NOT-KILLn) union GENn, where NOT-KILLn is the set of variables not defined at node n. The advantage of this formulation is that it permits the dataflow facts to be represented using bit vectors, and the dataflow functions to be implemented using simple bit-vector operations (and or).
It turns out that a number of interesting dataflow problems have dataflow functions of this same form, where GENn and KILLn are sets whose definition depends only on n, and the combining operator ⌈⌉ is either union or intersection. These problems are called GEN/KILL problems, or bit-vector problems.
Consider using dataflow analysis to determine which variables might be used before being initialized; i.e., to determine, for each point in the program, for which variables there is a path to that point on which the variable was never defined. Define the "may-be-uninitialized" dataflow problem by specifying:
- the domain D of "dataflow facts",
- the operator ⌈⌉,
- the "init" dataflow fact,
- a dataflow function for each CFG node n.
If you did not define the may-be-uninitialized problem as a GEN/KILL problem, go back and do that now (i.e., say what the GEN and KILL sets should be for each kind of CFG node, and whether ⌈⌉ should be union or intersection).
Solving a Dataflow Problem
A solution to an instance of a dataflow problem is a dataflow fact for each node of the given CFG. But what does it mean for a solution to be correct, and if there is more than one correct solution, how can we judge whether one is better than another?
Ideally, we would like the information at a node to reflect what might
happen on all possible paths to that node. This ideal solution is
called the meet over all paths (MOP) solution, and is
discussed below. Unfortunately, it is not always possible to compute
the MOP solution; we must sometimes settle for a solution that
provides less precise information.
The MOP solution (for a forward problem) for each CFG node n is
defined as follows:
For instance, in our running example program there are two paths from
the start of the program to line 9 (the assignment k = a):
Combining the information from both paths, we see that the MOP
solution for node 9 is: k=2 and a=4.
It is worth noting that even the MOP solution can be overly
conservative (i.e., may include too much information for a "may"
problem, and too little information for a "must" problem), because not
all paths in the CFG are executable. For example, a program may
include a predicate that always evaluates to false (e.g., a
programmer may include a test as a debugging device -- if the program
is correct, then the test will always fail, but if the program
contains an error then the test might succeed, reporting that error).
Another way that non-executable paths can arise is when two predicates
on the path are not independent (e.g., whenever the first evaluates to
true then so does the second). These situations are
illustrated below.
Unfortunately, since most programs include loops, they also have
infinitely many paths, and thus it is not possible to compute the MOP
solution to a dataflow problem by computing information for every path
and combining that information. Fortunately, there are other ways to
solve dataflow problems (given certain reasonable assumptions about
the dataflow functions associated with the CFG nodes). As we shall
see, if those functions are distributive, then the solution
that we compute is identical to the MOP solution. If the functions
are monotonic, then the solution may not be identical to the
MOP solution, but is a conservative approximation.
The alternative to computing the MOP solution directly, is to solve a
system of equations that essentially specify that local information
must be consistent with the dataflow functions. In particular, we
associate two dataflow facts with each node n:
One question is whether, in general, our system of equations will have
a unique solution. The answer is that, in the presence of loops,
there may be multiple solutions. For example, consider the simple
program whose CFG is given below:
The equations for constant propagation are as follows (where
⌈⌉ is the intersection combining operator):
The solution we want is solution 4, which includes the most constant
information. In general, for a "must" problem the desired solution
will be the largest one, while for a "may" problem the desired
solution will be the smallest one.
Using the simple CFG given above, write the equations for
live-variable analysis, as well as the greatest and least solutions.
Which is the desired solution, and why?
Many different algorithms have been designed for solving a dataflow
problem's system of equations. Most can be classified as either
iterative algorithms or elimination algorithms.
These two classes of algorithms are discussed in the next two
sections.
Most of the iterative algorithms are variations on the following
algorithm (this version is for forward problems).
It uses a new value T (called "top"). T has the property
that, for all dataflow facts d, T ⌈⌉ d = d.
Also, for all dataflow functions, fn(T) = T.
(When we consider the lattice model for dataflow analysis we will see
that this initial value is the top element of the lattice.)
Run this iterative algorithm on the simple CFG given above (the one with
a loop) to solve the constant propagation problem.
Run the algorithm again on the example CFG from the
examples section of the notes.
This algorithm works regardless of the order in which nodes are
removed from the worklist. However, that order can affect the
efficiency of the algorithm. A number of variations have been
developed that involve different ways of choosing that order.
When we consider the lattice model, we will revisit the question of
complexity.
Three important questions are:
The answers are provided by the framework first defined by Kildall.
The next section provides background on lattices;
the section after that presents Kildall's framework.
Definition:
Note: "partial" means it is not necessary that for all x,y in S,
either x ⊆ y or y ⊆ x.
It is OK for a pair of set elements to be incomparable.
Example 1:
The set S is the set of English words, and the ordering ⊆ is
substring (i.e., w1 ⊆ w2 iff w1 is a substring of w2).
Here is a picture of some words and their ordering (having an
edge w1 → w2 means w1 > w2).
Example 2:
S is the set of English words, and the ordering ⊆ is
"is shorter than or equal to in length".
Example 3:
S is the set of integers, and the ordering ⊆ is "less than or equal to".
This is a poset (try verifying each of the three properties).
Example 4:
S is the set of integers and the ordering ⊆ is "strictly less than".
This is not a poset, because the ordering is not reflexive.
Example 5:
S is the set of all sets of letters and the ordering is subset.
This is a poset.
Definition:
The "Meet Over All Paths" Solution

Solving a Dataflow Problem by Solving a Set of Equations
These n.befores and n.afters are the variables of our equations,
which are defined as follows (two equations for each node n):
In addition, we have one equation for the enter node:
where p1,
p2, etc are n's predecessors in the CFG (and ⌈⌉ is the
combining operator for this dataflow problem).
These equations make intuitive sense: the dataflow
information that holds before node n executes is the combination of
the information that holds after each of n's predecessors executes,
and the information that holds after n executes is the result of
applying n's dataflow function to the information that holds before n
executes.
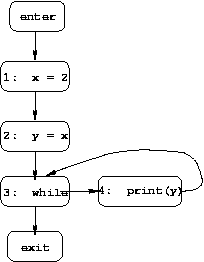
enter.after = empty set
Because of the cycle in the example CFG, the equations for
3.before, 3.after, 4.before, and
4.after are mutually recursive, which leads to the
four solutions shown below (differing on those four values).
1.before = enter.after
1.after = 1.before - (x, *) union (x, 2)
2.before = 1.after
2.after = if (x, c) is in 2.before then 2.before - (y, *) union (y, c), else 2.before - (y, *)
3.before = ⌈⌉(2.after, 4.after )
3.after = 3.before
4.before = 3.after
4.after = 4.before
Iterative Algorithms
Set enter.after = init. Set all other n.after to T.
Initialize a worklist to contain all CFG nodes except enter
and exit.
While the worklist is not empty:
Remove a node n from the worklist.
Compute n.before by combining all p.after such that p
is a predecessor of n in the CFG.
Compute
tmp = fn ( n.before )
If (tmp != n.after) then
Set n.after = tmp
Put all of n's successors on the worklist
The Lattice Model of Dataflow Analysis
Motivation
Recall that while we would like to compute the meet-over-all-paths (MOP)
solution to a dataflow problem, direct computation of that solution
(by computing and combining solution for every path) is usually not
possible.
Therefore, dataflow problems are usually solved by finding a solution
to a set of equations that define two dataflow facts (n.before and n.after)
for each CFG node n.
Background
Partially ordered sets
A partially ordered set (poset) is a set S that has a
partial ordering ⊆ , such that the ordering is:
Below are some examples of sets with orderings;
some are partially ordered sets and some are not.
candy then
/ \ / \
v v v v
annual and can the hen
\ | / \ /
\ | / v v
v v v he
an
|
v
a
Note that the "substring" ordering does have the three properties
required of a partial order:
candy
|
v
____ then
/ / | \
v v v v
can and the hen
\ \ / /
\ \ / /
v v v v
an
|
v
a
Does this ordering have the three properties?
Two out of three isn't good enough -- this is not a poset.
A lattice is a poset in which every pair of elements has:
The join of two elements x and y is defined to be the element z such that:
The first two rules say that z actually is an upper bound for
x and y, while the third rule says that z is the least
upper bound.
Pictorially:
z
/ \ z is the least upper bound of x and y
v v
y x
z w
|\/|
|/\| z is NOT the least upper bound of x and y
vv vv (they have NO least upper bound)
y z
The idea for the meet operation is similar, with the reverse orderings.
Examples:
Complete lattices
Definition:
-
A complete lattice is a lattice in which all subsets have
a greatest lower bound and a least upper bound (the bounds must be in
the lattice, but not necessarily in the subsets themselves).
Note: Every finite lattice (i.e., S is finite) is complete.
Examples:
- Example 3 above (integers, ordered by "less than or equal to")
is not a complete lattice.
The set of all positive numbers is a subset of S;
it has a lower bound but no upper bound.
The set of all even numbers is a subset of S; it has neither an upper nor a lower bound. - The set: {1, 1/2, 1/4, 1/8, ... 0} with the usual numeric ordering is an example of an infinite complete lattice.
Note: Every complete lattice has a greatest element, "Top" (written
as a capital T) and a least
element "Bottom" (written as an upside-down capital T).
They are the least-upper and the
greatest-lower bounds of the entire underlying set S.
Monotonic and distributive functions
Definition:
-
A function f: L → L (where L is a lattice)
is monotonic iff for all x,y in L:
x ⊆ y implies f(x) ⊆ f(y).
-
A function f: L → L (where L is a lattice)
is distributive iff for all x,y in L:
f(x meet y) = f(x) meet f(y).
Every distributive function is also monotonic (proving that could be good practice!) but not vice versa. For the GEN/KILL dataflow problems, all dataflow functions are distributive. For constant propagation, all functions are monotonic, but not all functions are distributive. For example, the dataflow function f associated with this assignment
-
x = a + b
| f(S) = | if S == T then T |
| else if (a, v1) in S and (b, v2) in S then S - (x,*) + (x, v1+v2) | |
| else S - (x,*) |