Abadie, Alberto, Susan Athey, Guido W Imbens, and Jeffrey M Wooldridge. 2020. “Sampling-Based Versus Design-Based Uncertainty in Regression Analysis.” Econometrica 88 (1): 265–96.
Buja, Andreas, Lawrence Brown, Richard Berk, Edward George, Emil Pitkin, Mikhail Traskin, Kai Zhang, and Linda Zhao. 2019. “Models as Approximations i.” Statistical Science 34 (4): 523–44.
Dawid, A Philip. 2000. “Causal Inference Without Counterfactuals.” Journal of the American Statistical Association 95 (450): 407–24.
Freedman, David. 2008. “On Regression Adjustments to Experimental Data.” Advances in Applied Mathematics 40 (2): 180–93.
Freedman, David, and David Lane. 1983. “A Nonstochastic Interpretation of Reported Significance Levels.” Journal of Business & Economic Statistics 1 (4): 292–98.
Hernán, Miguel, and James Robins. 2020. Causal Inference: What If. Boca Raton: Chapman & Hall/CRC.
Holland, Paul. 1986. “Statistics and Causal Inference.” Journal of the American Statistical Association 81 (396): 945–60.
Krieger, Nancy, and George Davey Smith. 2016. “The Tale Wagged by the DAG: Broadening the Scope of Causal Inference and Explanation for Epidemiology.” International Journal of Epidemiology 45 (6): 1787–1808.
Lehmann, Erich Leo. 2006. Nonparametrics: Statistical Methods Based on Ranks. Springer.
Lehmann, Erich L, and Joseph P Romano. 2006. Testing Statistical Hypotheses. Springer.
Li, Xinran, and Peng Ding. 2017. “General Forms of Finite Population Central Limit Theorems with Applications to Causal Inference.” Journal of the American Statistical Association 112 (520): 1759–69.
Lin, Winston. 2013. “Agnostic notes on regression adjustments to experimental data: Reexamining Freedman’s critique.” The Annals of Applied Statistics 7 (1): 295–318.
Neyman, Jerzy. 1923. “On the Application of Probability Theory to Agricultural Experiments. Essay on Principles. Section 9.” Statist. Sci. 5 (4): 465–72.
Robins, James M. 2002. “Covariance Adjustment in Randomized Experiments and Observational Studies: Comment.” Statistical Science 17 (3): 309–21.
Robins, James M, and Sander Greenland. 2000. “Causal Inference Without Counterfactuals: Comment.” Journal of the American Statistical Association 95 (450): 431–35.
Rosenbaum, Paul. 2002a. “Covariance Adjustment in Randomized Experiments and Observational Studies.” Statistical Science 17 (3): 286–327.
———. 2002b. Observational Studies. Springer.
Rosenbaum, Paul R. 1987. “The Role of a Second Control Group in an Observational Study.” Statistical Science 2 (3): 292–306.
Rubin, Donald B. 1974. “Estimating Causal Effects of Treatments in Randomized and Nonrandomized Studies.” Journal of Educational Psychology 66 (5): 688.
Shadish, W. R., T. D. Cook, and D. T. Campbell. 2002. Experimental and Quasi-Experimental Designs for Generalized Causal Inference. Houghton, Mifflin, & Company.
Suk, Youmi, and Hyunseung Kang. 2022. “Robust Machine Learning for Treatment Effects in Multilevel Observational Studies Under Cluster-Level Unmeasured Confounding.” Psychometrika 87 (1): 310–43.
Vandenbroucke, Jan P, Alex Broadbent, and Neil Pearce. 2016. “Causality and Causal Inference in Epidemiology: The Need for a Pluralistic Approach.” International Journal of Epidemiology 45 (6): 1776–86.
VanderWeele, Tyler J. 2016. “Commentary: On Causes, Causal Inference, and Potential Outcomes.” International Journal of Epidemiology 45 (6): 1809–16.
VanderWeele, Tyler J, and Whitney R Robinson. 2014. “On the Causal Interpretation of Race in Regressions Adjusting for Confounding and Mediating Variables.” Epidemiology 25 (4): 473–84.
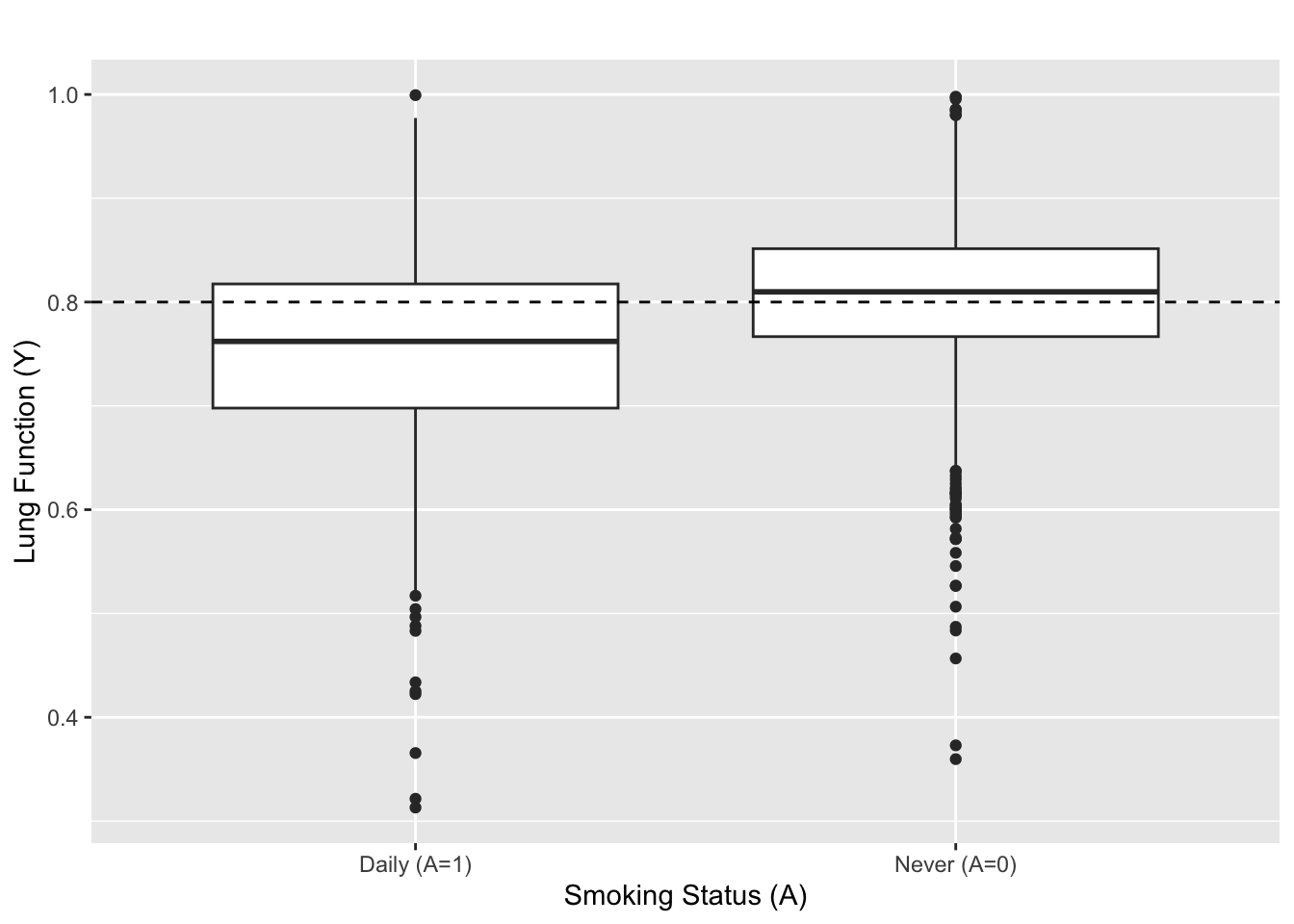
 Inspired by recent Marvel movies, I find the parallel universe analogy helpful to conceptualize causal effects.
Inspired by recent Marvel movies, I find the parallel universe analogy helpful to conceptualize causal effects.