


Next: Binary tree case
Up: Cache Placement
Previous: Cache Placement
We define the problem first.
Given a rooted tree with 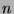 vertices. Every leaf
vertices. Every leaf 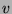 is associated with
a non-negative weight
is associated with
a non-negative weight ![$w[v]$](img66.png) . There are
. There are 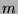 pebbles, where
pebbles, where 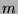 is
at most the number of leaves. Consider any placement of
up to
is
at most the number of leaves. Consider any placement of
up to 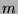 pebbles on any vertices of the tree. A placement of pebbles
is called feasible if every leaf
with a non-zero weight
pebbles on any vertices of the tree. A placement of pebbles
is called feasible if every leaf
with a non-zero weight ![$w[v] > 0$](img67.png) has an ancestor which has
a pebble on it. Here the ancestor relation is the reflexive and
transitive closure of the parent relation, in particular every vertex
is an ancestor of itself. The cost of any feasible placement
has an ancestor which has
a pebble on it. Here the ancestor relation is the reflexive and
transitive closure of the parent relation, in particular every vertex
is an ancestor of itself. The cost of any feasible placement 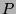 is defined as follows:
is defined as follows:
where the sum is over all leaves 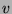 , and the cost associated with the leaf
, and the cost associated with the leaf 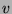 ,
denoted by
,
denoted by 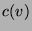 , is
, is
![$(\lambda +1) \cdot w[v]$](img71.png) ,
where
,
where 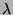 is the distance from
is the distance from 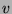 to the closest pebbled ancestor
of
to the closest pebbled ancestor
of 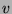 . Here the distance between two vertices of the tree
is the number of edges on the unique shortest path between them.
For technical reasons we define the cost of an infeasible placement
to be
. Here the distance between two vertices of the tree
is the number of edges on the unique shortest path between them.
For technical reasons we define the cost of an infeasible placement
to be 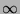 .
.
The goal is to find a feasible placement 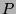 with at most
with at most 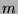 pebbles
such that
pebbles
such that 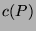 is minimized.
is minimized.



Next: Binary tree case
Up: Cache Placement
Previous: Cache Placement
Jim Gast
2001-04-20
![]() with at most
with at most ![]() pebbles
such that
pebbles
such that ![]() is minimized.
is minimized.